Oscillations II: Light and Critical Damping

Michael Fowler

Same Equation of Motion — Different Looking Solution

The equation of motion for the lightly damped oscillator is of course identical to that for the heavily damped case,

$m \frac{d^{2} x}{d t^{2}} = - k x - b \frac{d x}{d t} .$

and again we try solutions of the form

$x = x_{0} e^{- α t}$

finding

$α_{1}, α_{2} = \frac{b \pm \sqrt{b^{2} - 4 m k}}{2 m} .$

But the difference is that for light damping, by which we mean $b^{2} < 4 m k$ , the expression inside the square root is negative! Of course, we know this will give an answer circling (or spiralling) in the complex plane, and we will have to choose the real part. The complex root, then, is the key to actual oscillating behavior.

Writing:

$\sqrt{b^{2} - 4 m k} = i \sqrt{4 m k - b^{2}}$

with $i^{2} = - 1$ as usual, gives the two possible exponential solutions:

$x_{1} (t) = e^{- \frac{b t}{2 m}} e^{- \frac{i \sqrt{4 m k - b^{2}}}{2 m} t}, x_{2} (t) = e^{- \frac{b t}{2 m}} e^{+ \frac{i \sqrt{4 m k - b^{2}}}{2 m} t} .$

and a general solution

_{$x (t) = A_{1} e^{- \frac{b t}{2 m}} e^{- \frac{i \sqrt{4 m k - b^{2}}}{2 m} t} + A_{2} e^{- \frac{b t}{2 m}} e^{+ \frac{i \sqrt{4 m k - b^{2}}}{2 m} t} .$}

Of course, the position of the mass $x (t)$ has to be a real number! We must choose $A_{1}$ and $A_{2}$ to make sure that it is. Choosing

$A_{1} = \frac{1}{2} A e^{- i δ}, A_{2} = \frac{1}{2} A e^{+ i δ}$

where $A$ and $δ$ are real, and remembering

$\cos θ = \frac{1}{2} (e^{+ i θ} + e^{- i θ}),$

we get

$x (t) = A e^{- \frac{b t}{2 m}} \cos (\frac{\sqrt{4 m k - b^{2}}}{2 m} t + δ) .$

This is the most general real solution of the lightly damped oscillator $—$ the two arbitrary constants are the amplitude $A$ and the phase $δ .$ So for small $b,$ we get a cosine oscillation multiplied by a gradually decreasing function, $e^{- b t / 2 m} .$

This is often written in terms of a decay time $τ$ defined by

$τ = m / b .$

The amplitude of oscillation $A$ therefore decays in time as $e^{- t / 2 τ},$ and the energy of the oscillator (proportional to $A^{2}$ decays as $e^{- t / τ} .$ This means that in time $τ$ the energy is down by a factor $1 / e,$ with $e = 2.71828...$

The solution is sometimes written

$x (t) = A e^{- \frac{b t}{2 m}} \cos (ω^{'} t + δ)$

where

${ω^{'}}^{2} = \frac{4 m k - b^{2}}{4 m^{2}} = \frac{k}{m} - \frac{b^{2}}{4 m^{2}} = ω_{0}^{2} - \frac{b^{2}}{4 m^{2}} .$

Notice that for small damping, the oscillation frequency doesn’t change much from the undamped value: the change is proportional to the square of the damping.

The Q Factor: Ringing the Bell

The $Q$ factor is a measure of the “quality” of an oscillator (such as a bell): how long will it keep ringing once you hit it? Essentially, it is a measure of how many oscillations take place during the time the energy decays by the factor of $1 / e .$

$Q$ is defined by:

$Q = ω_{0} τ$

so, strictly speaking, it measures how many radians the oscillator goes around in time $τ$ . For a typical bell, $τ$ would be a few seconds, if the note is middle C, 256 Hz, that’s $ω_{0} = 2 π \times 256,$ so $Q$ would be of order a few thousand.

Exercise: estimate $Q$ for the following oscillator (and don’t forget the energy is proportional to the square of the amplitude):

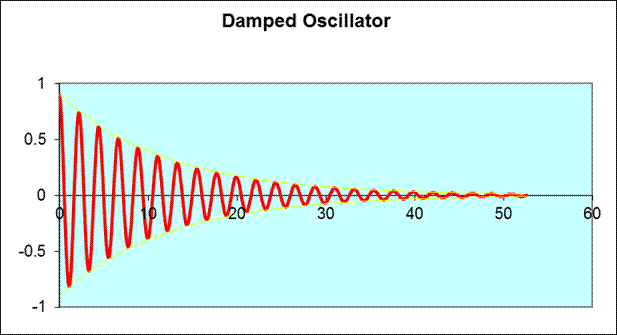
The yellow curves in the graph above are the pair of functions $+ e^{- b t / 2 m}, - e^{- b t / 2 m},$ often referred to as the envelope of the oscillation curve, as they “envelope” it from above and below.

Critical Damping: A Special Case

There is just one case we haven’t really discussed, and it’s called “critical damping”: what happens when $b^{2} - 4 m k$ is exactly zero? At first glance, that sounds easy to answer: there’s just the one solution

$x (t) = A e^{- \frac{b t}{2 m}} .$

But that’s not good enough $—$ it tells us that if we begin at $t = 0$ with the mass at $x_{0},$ it must have velocity $d x / d t$ equal to $- x_{0} b / 2 m .$ But, in fact, we can put the mass at $x_{0}$ and kick it to any initial velocity we want! So what happened to the other solution?

We can get a clue by examining the two exponentially falling solutions for the overdamped case as we approach critical damping:

$x (t) = A_{1} e^{- \frac{b + b \sqrt{1 - \frac{4 m k}{b^{2}}}}{2 m} t} + A_{2} e^{- \frac{b - b \sqrt{1 - \frac{4 m k}{b^{2}}}}{2 m} t}$

As we approach critical damping, the small quantity

$ε = \frac{\sqrt{b^{2} - 4 m k}}{2 m}$

approaches zero. The general solution to the equation has the form

$x (t) = e^{- \frac{b t}{2 m}} (A_{1} e^{- ε t} + A_{2} e^{+ ε t}) .$

This is a valid solution for any real $A_{1}, A_{2} .$ To find the solution we’re missing, the trick is to take $A_{2} = - A_{1} .$ In the limit of small $ε,$ , we can take $e^{ε t} = 1 + ε t,$ and we discover the solution

$x (t) = - e^{- \frac{b t}{2 m}} 2 ε t .$

As usual, we can always multiply a solution of a linear differential equation by a constant and still have a solution, so we write our new solution as

$x (t) = A_{2} t e^{- \frac{b t}{2 m}} .$

The general solution to the critically damped oscillator then has the form:

$x (t) = (A_{1} + A_{2} t) e^{- \frac{b t}{2 m}} .$

Exercise: check that this is a solution for the critical damping case, and verify that solutions of the form $t$ times an exponential don’t work for the other (noncritical damping) cases.

Should Your Shocks Be Critically Damped?

A shock absorber is basically a damped spring oscillator, the damping is from a piston moving in a cylinder filled with oil. Obviously, if the oil is very thin, there won’t be much damping, a pothole will cause your car to bounce up and down a few times, and shake you up. On the other hand, if the oil is really thick, or the piston too tight, the shock absorber will be too stiff $—$ it won’t absorb the shock, and you will! So we need to tune the damping so that the car responds smoothly to a bump in the road, but doesn’t continue to bounce after the bump.

Clearly, the “Damped Oscillator” graph in the $Q$ -factor section above corresponds to too little damping for comfort from a shock absorber point of view, such an oscillator is said to be underdamped. The opposite case, overdamping, looks like this:

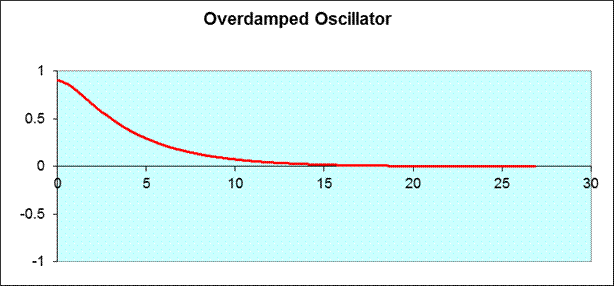
The dividing line between overdamping and underdamping is called critical damping. Keeping everything constant except the damping force from the graph above, critical damping looks like:

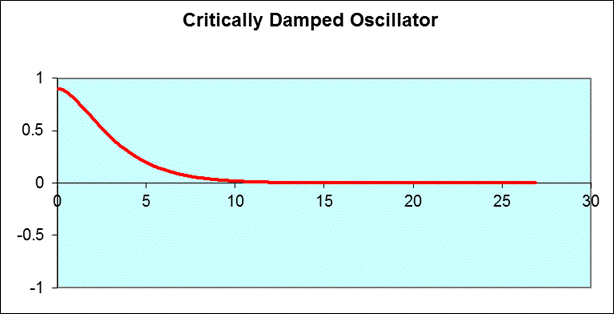
This corresponds to $ω^{'} = 0$ in the equation for $x (t)$ above, so it is a purely exponential curve. Notice that the oscillator moves more quickly to zero than in the overdamped (stiff oil) case.

You might think that critical damping is the best solution for a shock absorber, but actually a little less damping might give a better ride: there would be a slight amount of bouncing, but a quicker response, like this:

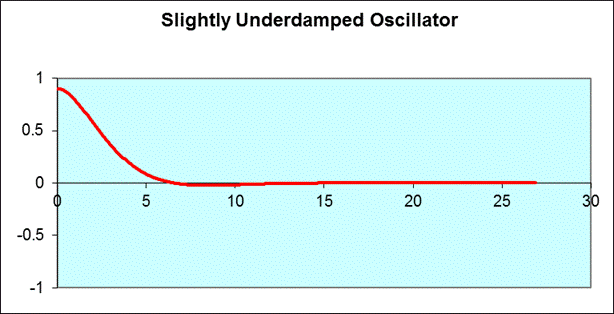
You can find out how your shock absorbers behave by pressing down one corner of the car and then letting go. If the car clearly bounces around, the damping is too little, and you need new shocks.

previous index next