The Gas Law and Avogadro's Hypothesis

Michael Fowler

Pressure, Volume, Temperature

The first step towards the Gas Law was Boyle's discovery, written up in 1662, that for a gas held at constant temperature, the pressure and volume were inversely related, $P V$ was constant.

Then, forty years later in 1702, Amontons established that for a gas held at constant volume, the pressure increased linearly with temperature, at least in the temperature range between the freezing point of water and its boiling point.

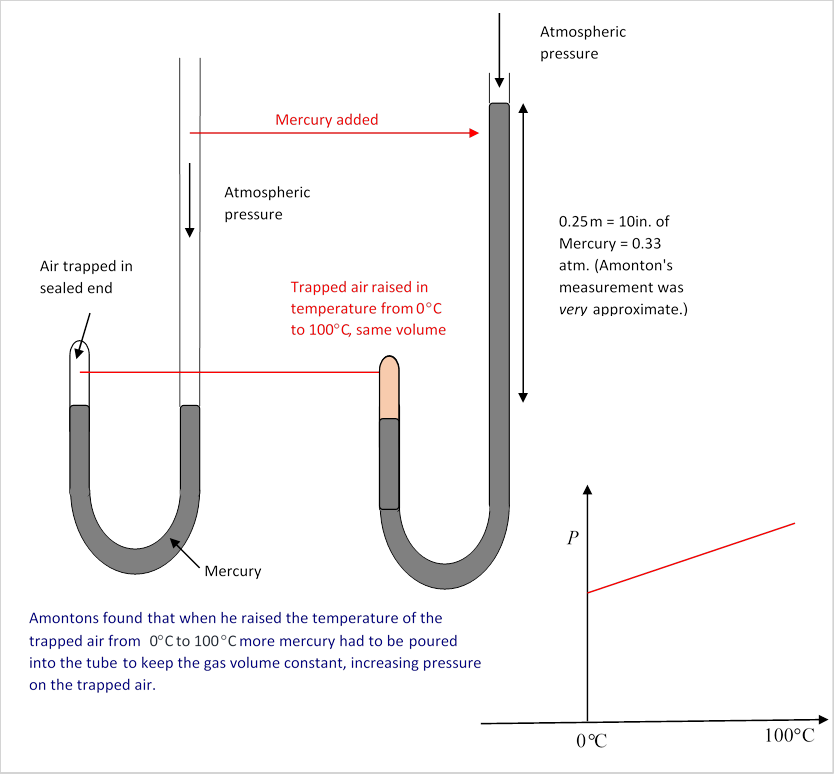
That is to say, Amontons discovered (with equipment a lot like Boyle's) that if a container of air were to be sealed at 0°C, at ordinary atmospheric pressure of 15 pounds per square inch, and then heated to 100°C but kept at the same volume, the air would now exert a pressure of about 20 pounds per square inch on the sides of the container. (Of course, strictly speaking, the container will also have increased in size, that would lower the effect $—$ but it’s a tiny correction, about $½$ % for copper, even less for steel and glass.)

He went on to establish that if the gas were initially at a pressure of thirty pounds per square inch at 0°C, on heating to 100°C the pressure would go to about 40 pounds per square inch $—$ so the percentage increase in pressure was the same for any initial pressure: on heating through 100°C, the pressure would always increase by about 33%. Furthermore, the result turned out to be the same for different gases!

His actual Boyle-style experiment, diagrammed here, had a small volume of air trapped in a closed-end arm of a U-tube, the other taller arm was open, and by pouring mercury into that arm the pressure on the trapped air could be adjusted. The small volume of trapped air could be surrounded by a container, first filled with an ice/water mix, then boiling water. In each case, measurements need to be taken over time to ensure the trapped air has reached a steady temperature. (Note: It's not clear to me how or if he established intermediate temperatures, this was before mercury thermometers. Need to find out.)

Actually we repeated this in class (admittedly with a modern pressure gauge and thermometer). We plotted air pressure as a function of temperature for a fixed volume of air, by making several measurements as the air was slowly heated (to give it a chance to all be at the same temperature at each stage). We found a straight line.

Then, on the graph, we extended the line backwards, to see how the pressure would drop on cooling the air.

Finding a Natural Temperature Scale

We found (more accurately than Amontons had managed) the remarkable prediction that the pressure should drop to zero at a temperature of about -273°C.

In fact, if we’d done the cooling experiment, we would have found that air doesn’t actually follow the line all the way down, but condenses to a liquid at around -200°C. However, helium gas stays a gas almost to -270°C, and follows the line closely to that point.

We shall discuss the physics of gases, and the interpretation of this, much more fully in a couple of lectures. For now, the important point is that this suggests a much more natural temperature scale than the Celsius one: we should take -273°C as the zero of temperature! For one thing, if we do that, the pressure/temperature relationship for a gas becomes beautifully simple:

$P \propto T .$

This temperature scale, in which the degrees have the same size as in Celsius, is called the Kelvin or absolute scale. Temperatures are written 300K. To get from Celsius to Kelvin, just add 273 (strictly speaking, 273.15).

An Ideal Gas

Physicists at this point introduce the concept of an “Ideal Gas”. This is like the idea of a frictionless surface: it doesn’t exist in nature, but it is a very handy approximation to some real systems, and makes problems much easier to handle mathematically. The ideal gas is one for which $P \propto T$ for all temperatures, so helium is close to ideal over a very wide range, and air is close to ideal at ordinary atmospheric temperatures and above.

The Gas Law

We saw earlier in the course that for a gas at constant temperature $P V =$ constant (Boyle’s Law).

Now from Amontons, at constant volume, $P \propto T$ .

We can put these together into one equation to find a relationship between pressure, volume and temperature:

$P V = C T$

where $C$ is a constant. Notice, by the way, that we can immediately conclude that at fixed pressure, $V \propto T$ , this is called Charles’ Law. (Exercise: prove from this that the coefficient of volume expansion of a gas varies significantly with temperature.)

But what is $C$ ? Obviously, it depends on how much gas we have $—$ double the amount of gas, keeping the pressure and temperature the same, and the volume will be doubled, so $C$ will be doubled. But notice that $C$ will not depend on what gas we are talking about: if we have two separate one-liter containers, one filled with hydrogen, the other with oxygen, both at atmospheric pressure, and both at the same temperature, then $C$ will be the same for both of them.

One might conclude from this that $C$ should be defined for one liter of gas at a specified temperature and pressure, such as 0°C and 1 atmosphere, and that could be a consistent scheme. It might seem more natural, though, to specify a particular mass of gas, since then we wouldn’t have to specify a particular temperature and pressure in the definition of $C .$

But that idea brings up a further problem: one gram of oxygen takes up a lot less room than one gram of hydrogen. Since we’ve just seen that choosing the same volume for the two gases gives the same constant $C$ for the two gases, evidently taking the same mass of the two gases will give different $C$ ’s.

Avogadro’s Hypothesis

The resolution to this difficulty is based on a remarkable discovery the chemists made two hundred years or so ago: they found that one liter of nitrogen could react with exactly one liter of oxygen to produce exactly two liters of NO, nitrous oxide, all volume measurements being at the same temperature and pressure. Further, one liter of oxygen combined with two liters of hydrogen to produce two liters of steam.

These simple ratios of interacting gases could be understood if one imagined the atoms combining to form molecules, and made the further assumption, known as Avogadro’s Hypothesis (1811):

Equal volumes of gases at the same temperature and pressure contain the same number of molecules.

One could then understand the simple volume results by assuming the gases were made of diatomic molecules, H₂, N₂, O₂ and the chemical reactions were just molecular recombinations given by the equations N₂ + O₂ = 2NO, 2H₂ + O₂ = 2H₂O, etc.

Of course, in 1811 Avogadro didn’t have the slightest idea what this number of molecules was for, say, one liter, and nobody else did either, for another fifty years. So no-one knew what an atom or molecule weighed, but assuming that chemical reactions were atoms combining into molecules, or rearranging from one molecular pairing or grouping to another, they could figure out the relative weights of atoms, such as an oxygen atom had mass 16 times that of a hydrogen atom $—$ even though they had no idea how big these masses were!

This observation led to defining the natural mass of a gas for setting the value of the constant $C$ in the gas law to be a “mole” of gas: hydrogen was known to be H₂ molecules, so a mole of hydrogen was 2 grams, oxygen was O₂, so a mole of oxygen was 32 grams, and so on.

With this definition, a mole of oxygen contains the same number of molecules as a mole of hydrogen: so at the same temperature and pressure, they will occupy the same volume. At 0°C, and atmospheric pressure, the volume is 22.4 liters.

So, for one mole of a gas (for example, two grams of hydrogen), we set the constant $C$ equal to $R,$ known as the universal gas constant, and equal to 8.3 J/(mol.K) and $P V = R T .$

For n moles of a gas, such as 2n grams of hydrogen, the law is:

$P V = n R T$

and this is the standard form of the Gas Law.

(Footnote: after the discovery of isotopes, nuclei of the same element having different masses, and in particular of a form of hydrogen called heavy hydrogen present in small quantities in nature, the definition of the mole was refined to be equal to precisely 12 grams of the carbon isotope C¹². In practice, this is a tiny correction which doesn’t affect anything we’ve said here.)

previous index next PDF