The Simple Harmonic Oscillator

Michael Fowler, University of Virginia

Einstein’s Solution of the Specific Heat Puzzle

The simple harmonic oscillator, a nonrelativistic particle in a potential ½Cx², is a system with wide application in both classical and quantum physics. The simplest model is a mass sliding backwards and forwards on a frictionless surface, attached to a fixed wall by a spring, the rest position defined by the natural length of the spring.

Many of the mechanical properties of a crystalline solid can be understood by visualizing it as a regular array of atoms, a cubic array in the simplest instance, with nearest neighbors connected by springs (the valence bonds) so that an atom in a cubic crystal has six such springs attached, parallel to the x, y, and z axes. Provided the oscillations of the atoms are not too large, the springs behave well, and the atom sees itself in a potential .

Now, as the solid is heated up, it should be a reasonable first approximation to take all the atoms to be jiggling about independently, and classical physics, the “Equipartition of Energy”, would then assure us that at temperature T each atom would have on average energy 3kT, k being Boltzmann’s constant. The specific heat per atom would then be just 3k.

But this is not what is observed! The specific heats of all solids drop dramatically at low temperatures. What’s going on here? It took Einstein to figure it out. Recall in the earlier lecture on Black Body Radiation that at low temperatures the blue modes were frozen out because energy could only be absorbed or emitted in quanta, photons, and the energy per quantum was directly proportional to the frequency, so only relatively low energy oscillators gained energy at low temperatures.

Einstein realized that exactly the same considerations must apply to mechanical oscillators, such as atoms in a solid. He assumed each atom to be an independent simple harmonic oscillator, and, just as in the case of black body radiation, the oscillators can only absorb energies in quanta. Consequently, at low enough temperatures there is rarely sufficient energy in the ambient thermal excitations to excite the oscillators, and they freeze out, just like blue oscillators in low temperature black body radiation. Einstein’s picture was later somewhat refined—the basic set of oscillators was taken to be standing sound wave oscillations in the solid rather than individual atoms (even more like black body radiation in a cavity) but the main conclusion was not affected. In the more modern picture of sound waves in a solid, the “elementary” sound wave, analogous to the photon, is called the phonon, and has energy hf, where h is again Planck’s constant, and f is the sound frequency.

Oscillations of molecules can usually be analyzed fairly accurately as simple harmonic oscillations, in particular the diatomic molecule. Of course, this picture breaks down for sufficiently large amplitude oscillations—eventually any molecule breaks up.

Wave Functions for Oscillators

What kind of wave function do we expect to see in a harmonic oscillator potential? Whatever kinetic energy we give the particle, if it gets far enough from the origin the potential energy will win out, and the wave will decay for the particle going further out. We know that when a particle penetrates a barrier of height V₀, say, greater than the particle’s kinetic energy, the wave function decreases exponentially into the barrier, like , where . But the simple harmonic oscillator potential is less penetrable than a flat barrier, because its height increases as x² as the particle penetrates, so we can see from the expression for a above that for large x a itself increases linearly in x. Of course, this is something of a handwaving argument, the solution of a differential equation for a varying potential is not just a smooth sequence of solutions for constant potentials, but it does suggest that the right wavefunction for the oscillator potential might decay as . We write it as , so that the probability distribution is proportional to , and a, which has the dimensions of length, is a natural measure of the spread of the wave function.

The Schrödinger equation for the simple harmonic oscillator is

If , it is straightforward to verify that

Substituting this value in Schrödinger’s equation we find

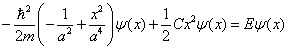
This equation can only be true for all x if the x² terms are separately identically zero, that is,

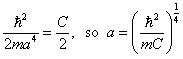This fixes the wave function. Requiring the remaining terms to balance fixes the energy:

where w₀ is the classical oscillator frequency—given the particle mass m and the spring constant C, the classical equation of motion of the oscillator is

Taking a solution of the form

gives .

An important point here is that the energy is nonzero, just as it was for the square well. The central part of the wave function must have some curvature to join together the decreasing wave function on the left to that on the right. This “zero point energy” is sufficient in one case to melt the lattice—helium is liquid even down to absolute zero temperature (checked down to microkelvins!) because of this wave function spread.

Using the Spreadsheet

The spreadsheet can be used to find the energies of the eigenstates of the simple harmonic oscillator in a very similar way to those for the square well. One technical difference is that since the exponential increasing function diverges more violently, it is almost impossible to avoid it becoming dominant at large x. However, provided the wave function is small over some range in x, in practice wave functions and energies are given quite accurately. One point worth noting is that just as for the square well, the quantum number for the states is just the number of nodes, or zeros. The argument we gave for the square well about how the extra nodes come into the wave function as the energy is increased also works here.

For readers who have not at this point constructed the spreadsheet, which is a very educational exercise you should do at some point, you can download and play with one for the simple harmonic oscillator here: DOWNLOAD SPREADSHEET .

Time Dependent States of the Simple Harmonic Oscillator

Working with the time independent Schrödinger equation, as we have in the above, implies that we are restricting ourselves to solutions of the full Schrödinger equation which have a particularly simple time dependence, an overall phase factor , and are states of definite energy E. However, the full time dependent Schrödinger equation is a linear equation, so if ψ₁(x,t) and ψ₂(x,t) are solutions, so is any linear combination Aψ₁+Bψ₂. Assuming ψ₁ and ψ₂ are definite energy solutions for different energies E₁ and E₂, the combination will not correspond to a definite energy—a measurement of the energy will give either E₁ or E₂, with appropriate probabilities. In the jargon, the combination is not an “eigenstate” of the energy—but it is still a perfectly good, physically realizable wave function.

It is instructive to examine a combination state of this form a little more closely. We know that for the ground state wave function,

and for the first excited state,

Suppose we simply add terms of this type together (neglecting the overall normalization constant for now), for example

Looking at this wave function for t = 0, we notice that the two terms have the same sign for x > 0, and opposite signs for x < 0. Therefore, sketching the probability distribution for the particle’s position, it is heavily skewed to the right (positive x). However, the two terms have different time-dependent phases, differing by a factor , so after time has elapsed, a factor of -1 has evolved between the terms. If we now look at the probability distribution |ψ|², it will be skewed to the left. In other words, if the state is not of definite energy, the probability distribution can vary in time. Of course, the total probability of finding the particle somewhere stays the same. Note that the probability distribution swings back and forth with the period of the oscillator. This discussion also implies that an ordinary pendulum, which clearly swings back and forth, cannot be in a state of definite energy!

The Three Dimensional Simple Harmonic Oscillator

It is very simple to go from the one dimensional to the three dimensional simple harmonic oscillator, because the potential is a sum of separate x, y, z potentials, and consequently any product of three solutions of the one- dimensional harmonic oscillator time independent Schrödinger equation will be a solution of the three-dimensional harmonic oscillator, with energy the sum of the three one-dimensional energies. So the states are labeled with three quantum numbers, one for each direction, each can be 0, 1, 2, … If we call these three quantum numbers n_x, n_y, n_z then from what we already know about the one dimensional case, the energy of the three dimensional state must be . For example, the lowest energy state of the three dimensional harmonic oscillator, the zero point energy, is . Obviously, the higher energy states are very degenerate—many sets of quantum numbers correspond to the same state—because the energy only depends on the sum of the three integer quantum numbers. Note that this degeneracy arises from the symmetry of the potential, the spring constant k is the same in all three directions. If the potential were of the form for general k’s, there would be no degeneracy. (Such potentials approximately describe oscillations of an atom in an anisotropic crystal.)

Another approach to the three dimensional symmetric ½kr² simple harmonic oscillator is to try a separable wave function in spherical polar coordinates, . This approach is covered in detail in later courses in quantum mechanics, and is the standard method for treating the hydrogen atom (where the potential cannot be written as a sum of x, y, and z potentials). The angular functions describe the angular momentum of the particle. Some insight can be gained by considering the two dimensional case. Consider a pendulum swinging in the x direction (z is vertical). Now give it a kick so it also has swing in the y direction. In general, it will follow an elliptical path in the x, y plane. The right kick will make it a circle. For the circular orbit, the old fashioned Bohr quantization of angular momentum can be used to find the energy levels.

previous home next PDF