Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
Our analysis of the time independent Schrödinger equation using
the spreadsheet limited us to real values of the wave function psi(x).
This is fine for analyzing bound states in a potential, or standing waves
in general, but cannot be used, for example, to represent a stream of electrons
being emitted by an electron gun, such as in a TV tube. The reason is that
a real-valued wave function psi(x), in an energetically allowed
region, is made up of terms locally like coskx and sinkx,
multiplied in the full wave function by the time dependent phase factor
, giving equal amplitudes of
right moving waves
and left
moving waves
. So if we are
interested in a system in which there are not equal numbers of particles
moving to the right and to the left, we must have a wave function such
that even the x-dependent part is complex.
A simple example is a stream of particles of energy E moving
from the left in one dimension through a region of zero potential, encountering
an upward step potential V0 at the origin x =
0, where V0 < E, so that classically the particles
would climb the hill and continue to the right. We shall represent the
incoming wave function by a plane wave,
for x <
0
(it proves slightly more convenient to work with wave number k
rather than particle momentum in scattering problems of this type). If
we now think of the classical picture of a particle approaching a hill
(smoothing off the corners a bit) that it definitely has enough energy
to surmount, we would perhaps expect that the wave function continues beyond
x = 0 in the form
for x >
0,
where k1 corresponds to the slower speed the particle
will have after climbing the hill.
Schrödinger's equation requires that the wave function have no
discontinuities and no kinks (discontinuities in slope) so the x
< 0 and x > 0 wave functions must match smoothly at the origin.
For them to have the same value, we see from above that A = B.
For them to have the same slope we must have kA = k1B.
Unfortunately, the only way to satisfy both these equations with our above
wave functions is to take k = k1-which means there
is no step potential at all!
Question: what is wrong with the above reasoning?
The answer is that we have been led astray by our mental picture of
the particles as little balls rolling along in a potential, with enough
energy to get up the hill, etc. Schrödinger's equation is a wave
equation. Building intuition about solutions should rely on experience
with waves. We should be thinking about a light wave going from
air into glass, for example. If we do, we realize that at any interface
some of the light gets reflected. This means that our expression
for the wave function for x < 0 is incomplete, we need to add
a reflected wave, giving
for x <
0
for x >
0.
If we now match the wave function and its derivative at the origin,
we find
A + C = B
k(A - C) = k1B.
Recalling that the square of the wave function denotes probability,
it is easy to check that the fraction of the wave that is reflected
Evidently, the fraction of the wave transmitted
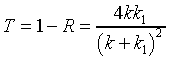
Question: isn't the amount transmitted just given by B2/A2?
The answer is no. The ratio B2/A2
gives the relative probability of finding a particle in some small region
in the transmitted stream relative to that in the incoming stream, but
the particles in the transmitted stream are moving more slowly, by a factor
k1/k. That means that just comparing the densities
of particles in the transmitted and incoming streams is not enough. The
physically significant quantity is the probability current flowing
past a given point, and this is the product of the density and the
speed. Therefore, the transmission coefficient is B2k1/A2k.
Exercise: prove that even a step down gives rise to some
reflection.
If a plane wave coming in from the left encounters a step at the origin
of height V0 > E, the incoming energy, there
will be total reflection, but with an exponentially decaying wave penetrating
some distance into the step. Suppose now we replace the step with a barrier,
V = 0 for x < 0
V = V0 for 0 < x < L
V = 0 for L < x.
In this situation, the wave function will still decay exponentially into the barrier (assuming the barrier is thick compared to the exponential decay length), but on reaching the far end at x = L, a plane wave solution is again allowed, so there is a nonzero probability of finding the particle beyond the barrier, moving with its original speed. This phenomenon is called tunneling, since in the classical picture the particle doesn't have enough energy to get over the top of the barrier.
A good example of tunneling, and one which helped establish the validity
of quantum ideas at the nuclear level, is alpha decay. Certain large
unstable nuclei decay radioactively by emitting an alpha particle, a tightly
bound state of two protons and two neutrons. It is thought that alpha particles
may exist, at least as long lived resonances, inside the nucleus. For such
a particle, the strong but short ranged nuclear force creates a spherical
finite depth well having a steep wall more or less coinciding with the
surface of the nucleus. However, we must also include the electrostatic
repulsion between the alpha-particle and the rest of the nucleus, a potential
outside the nucleus. This
means that, as seen from inside the nucleus, the wall at the surface may
not be a step but a barrier, in the sense we used the word above, a step
up followed by a slide down the electrostatic curve. Therefore, an alpha-particle
bouncing around inside the nucleus may have enough energy to tunnel through
to the outside world.
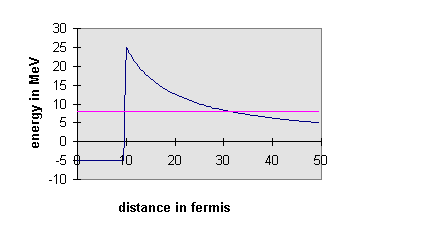
It is evident that the more energetic the alpha-particle is, the thinner
the barrier it faces. Since the wave function decays exponentially in the
barrier, this can make a huge difference in tunneling rates. It is not
difficult to find the energy with which the alpha-particle hits the nuclear
wall, because this will be the same energy with which it escapes. Therefore,
if we measure the energy of an emitted alpha, since we think we know the
shape of the barrier pretty well, we should be able, at least numerically,
to predict the tunneling rate. The only other thing we need to know is
how many times per second alpha's bounce off the wall. The size of the
nucleus is of order 10-14 meters, if we assume an alpha moves
at, say, 107 meters per second, it will bang into the wall 1021
times per second. This is a bit handwaving, but all alpha-radioactive nuclei
are pretty much the same size, so perhaps it's safe to assume this will
be about the same for all of them. If we do that, we get impressive agreement
with experiment over a huge range of lifetimes. polonium212
emits alpha's with energy 8.95 MeV, and lasts 3 10-7 seconds,
thorium232 emits 4.05 MeV alpha's, and lasts 1.4 1010 years.
These can both be understood in terms of essentially the same barrier being
tunneled through at the different heights corresponding to the alpha energy.
(French, QM, page 407).
Exercise: assume the nucleus has a charge of 90e, and a radius of 10-14 meters. Estimate the height of the barrier at its maximum, and the width of barrier an alpha must tunnel through for polonium and thorium, discussed above. (Of course, the tunneling rate is not the same as for a rectangular barrier-one must include the variation of the decay length with the changing barrier height. This is the main part of the so-called WKB approximation, see any book on quantum mechanics.)