The Simple Harmonic Oscillator
Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
Einstein's Solution of the Specific Heat Puzzle
The simple harmonic oscillator, a nonrelativistic particle in
a potential ½Cx2, is a system with wide
application in quantum physics. Einstein was the first to understand
why the specific heats of all solids drop dramatically at low
temperatures. He assumed each atom to be an independent simple
harmonic oscillator, and, just as in the case of black body radiation,
the oscillators can only absorb energies in quanta. Consequently,
at low enough temperatures there is rarely sufficient energy in
the ambient thermal excitations to excite the oscillators, and
they freeze out, just like blue oscillators, say, in low temperature
black body radiation. Einstein's picture was later somewhat refined-the
basic set of oscillators was taken to be standing sound wave oscillations
in the solid rather than individual atoms (even more like black
body radiation in a cavity) but the main conclusion was not affected.
Wave Functions for Oscillators
What kind of wave function do we expect to see in a harmonic oscillator
potential? Whatever kinetic energy we give the particle, if it
gets far enough from the origin the potential energy will win
out, and the wave will decay for the particle going further out.
We know that when a particle penetrates a barrier of height V0,
say, greater than the particle's kinetic energy, the wave function
decreases exponentially into the barrier, like 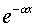 ,
where
,
where 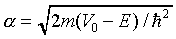 . But the simple harmonic oscillator
potential is less penetrable than a flat barrier, because its
height increases as x2 as the particle penetrates
to large x. It follows from the expression for alpha above
that for large x alpha itself increases linearly
in x. Of course, this is something of a hand waving argument,
the solution of a differential equation for a varying potential
is not just a smooth sequence of solutions for constant potentials,
but it does suggest that the right wave function for the oscillator
potential might decay as
. But the simple harmonic oscillator
potential is less penetrable than a flat barrier, because its
height increases as x2 as the particle penetrates
to large x. It follows from the expression for alpha above
that for large x alpha itself increases linearly
in x. Of course, this is something of a hand waving argument,
the solution of a differential equation for a varying potential
is not just a smooth sequence of solutions for constant potentials,
but it does suggest that the right wave function for the oscillator
potential might decay as  . We write it
as
. We write it
as  , so that the probability distribution
is proportional to
, so that the probability distribution
is proportional to 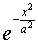 , and a, which
has the dimensions of length, is a natural measure of the spread
of the wave function.
, and a, which
has the dimensions of length, is a natural measure of the spread
of the wave function.
The Schrödinger equation for the simple harmonic oscillator
is
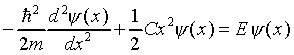
If 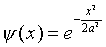 , it is straightforward to verify that
, it is straightforward to verify that
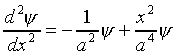
Substituting this value in Schrödinger's equation we find


This equation can only be true for all x if the x2
terms are separately identically zero, that is,
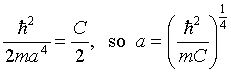 .
.
This fixes the wave function. Requiring the remaining terms to
balance fixes the energy:
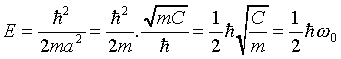 ,
,
where omega_zero is the classical oscillator frequency-given
the particle mass m and the spring constant C, the
classical equation of motion of the oscillator is
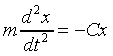 .
.
Taking a solution of the form
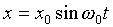 ,
,
gives  .
.
Notice that we have verified that our conjectured form for the
wave function is in fact the exact solution for the lowest
energy state! The first excited state has a wave function proportional
to 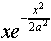 , and higher states have the x
replaced by a sequence of polynomials in x (called the
Hermite polynomials).
, and higher states have the x
replaced by a sequence of polynomials in x (called the
Hermite polynomials).
An important point here is that even in the lowest state-the ground
state-the energy is nonzero, just as it was for the square well.
The central part of the wave function must have some curvature
to join together the decreasing wave function on the left to that
on the right. This "zero point energy" is sufficient
in one case to melt the lattice-helium is liquid even down to
absolute zero temperature (checked down to microkelvins!) because
of this wave function spread.
It is interesting to note that although the wave functions become
quite complicated for the higher states, the energy levels have
a very simple pattern-they are all equally spaced: 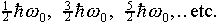 The simple harmonic oscillator is the only potential having uniformly
spaced energy levels.
The simple harmonic oscillator is the only potential having uniformly
spaced energy levels.
Exercise: How is the uniform energy level spacing related
to the fact that the classical simple harmonic oscillator
is the only potential where the period of oscillation of the trapped
particle is independent of the amplitude of oscillation?
Using the Spreadsheet
The spreadsheet can be used to find the energies of the eigenstates
of the simple harmonic oscillator in a very similar way to those
for the square well. One technical difference is that the "wrong"
solution to Schrödinger's equation, the one that increases
on going away from the well, does so more violently, and it is
almost impossible to avoid its becoming dominant at large x.
However, provided the wave function is small over some finite
range in x, in practice wave functions and energies are
given quite accurately. This will become clearer with practice.
One point worth noting is that just as for the square well, the
quantum number for the states is just the number of nodes, or
zeros. The argument we gave for the square well about how the
extra nodes come into the wave function as the energy is increased
also works here.
Time Dependent States of the Simple Harmonic Oscillator
Working with the time independent Schrödinger equation, as
we have in the above, implies that we are restricting ourselves
to solutions of the full Schrödinger equation which have
a particularly simple time dependence, an overall phase factor
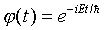 , and are states of definite energy E.
However, the full time dependent Schrödinger equation is
a linear equation, so if psi1(x,t)
and psi2(x,t) are solutions, so
is any linear combination Apsi1+Bpsi2.
Assuming psi1 and psi2 are
definite energy solutions for different energies E1
and E2, the combination will not correspond
to a definite energy-a measurement of the energy will give either
E1 or E2, with appropriate
probabilities. In the jargon, the combination is not an "eigenstate"
of the energy-but it is still a perfectly good, physically realizable
wave function.
, and are states of definite energy E.
However, the full time dependent Schrödinger equation is
a linear equation, so if psi1(x,t)
and psi2(x,t) are solutions, so
is any linear combination Apsi1+Bpsi2.
Assuming psi1 and psi2 are
definite energy solutions for different energies E1
and E2, the combination will not correspond
to a definite energy-a measurement of the energy will give either
E1 or E2, with appropriate
probabilities. In the jargon, the combination is not an "eigenstate"
of the energy-but it is still a perfectly good, physically realizable
wave function.
It is instructive to examine a combination state of this form
a little more closely. We know that for the ground state wave
function,
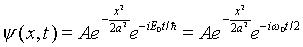
and for the first excited state,
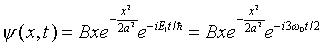 .
.
Suppose we simply add terms of this type together (neglecting
the overall normalization constant for now), for example
 .
.
Looking at this wave function for t = 0, we notice that
the two terms have the same sign for x > 0, and opposite
signs for x < 0. Therefore, sketching the probability
distribution for the particle's position, it is heavily skewed
to the right (positive x). However, the two terms have
different time-dependent phases, differing by a factor 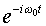 ,
so after time pi/omega_zero has elapsed, a factor
of -1 has evolved between the terms. If we now look at
the probability distribution |psi|2, it will
be skewed to the left. In other words, if the state is not of
definite energy, the probability distribution can vary in time.
Of course, the total probability of finding the particle
somewhere stays the same. Note that the probability distribution
swings back and forth with the period of the oscillator. This
discussion also implies that an ordinary pendulum, which clearly
swings back and forth, cannot be in a state of definite energy!
,
so after time pi/omega_zero has elapsed, a factor
of -1 has evolved between the terms. If we now look at
the probability distribution |psi|2, it will
be skewed to the left. In other words, if the state is not of
definite energy, the probability distribution can vary in time.
Of course, the total probability of finding the particle
somewhere stays the same. Note that the probability distribution
swings back and forth with the period of the oscillator. This
discussion also implies that an ordinary pendulum, which clearly
swings back and forth, cannot be in a state of definite energy!
The Three Dimensional Simple Harmonic Oscillator
It is very simple to go from the one dimensional to the three
dimensional simple harmonic oscillator, because the potential
½kr2 = ½kx2 + ½ky2
+ ½kz2 is a sum of separate x, y,
z potentials, and consequently any product psi(x,y,z)
= f(x)g(y)h(z) of three
solutions of the one dimensional harmonic oscillator time independent
Schrödinger equation will be a solution of the three dimensional
harmonic oscillator, with energy the sum of the three one dimensional
energies. So the states are labeled with three quantum numbers,
one for each direction, each can be 0, 1, 2, … If we call
these three quantum numbers nx, ny,
nz then from what we already know about the
one dimensional case, the energy of the three dimensional state
must be 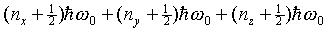 . For example, the lowest energy
state of the three dimensional harmonic oscillator, the zero point
energy, is
. For example, the lowest energy
state of the three dimensional harmonic oscillator, the zero point
energy, is 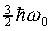 . Obviously, the higher energy
states are very degenerate-many sets of quantum numbers correspond
to the same state-because the energy only depends on the sum
of the three integer quantum numbers. Note that this degeneracy
arises from the symmetry of the potential, the spring constant
k is the same in all three directions. If the potential
were of the form ½k1x2
+ ½k2y2 + ½k3z2,
for general k's, there would be no degeneracy. (Such potentials
approximately describe oscillations of an atom in an anisotropic
crystal.)
. Obviously, the higher energy
states are very degenerate-many sets of quantum numbers correspond
to the same state-because the energy only depends on the sum
of the three integer quantum numbers. Note that this degeneracy
arises from the symmetry of the potential, the spring constant
k is the same in all three directions. If the potential
were of the form ½k1x2
+ ½k2y2 + ½k3z2,
for general k's, there would be no degeneracy. (Such potentials
approximately describe oscillations of an atom in an anisotropic
crystal.)
Another approach to the three dimensional ½kr2
simple harmonic oscillator is to try a separable wave function
in spherical polar coordinates,
 .
.
This approach is covered in detail in later courses in quantum
mechanics, and is the standard method for treating the hydrogen
atom (where the potential cannot be written as a sum of x,
y, and z potentials). The angular functions describe
the angular momentum of the particle. Some insight can be gained
by considering the two dimensional case. Consider a pendulum swinging
in the x direction (z is vertical). Now give it
a kick so it also has swing in the y direction. In general,
it will follow an elliptical path in the x, y plane.
The right kick will make it a circle. For the circular orbit,
the old fashioned Bohr quantization of angular momentum can be
used to find the energy levels.
Physics 252 Home Page
Link to Next Lecture
Copyright ©1997 Michael Fowler
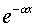 ,
where
,
where 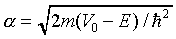 . But the simple harmonic oscillator
potential is less penetrable than a flat barrier, because its
height increases as x2 as the particle penetrates
to large x. It follows from the expression for alpha above
that for large x alpha itself increases linearly
in x. Of course, this is something of a hand waving argument,
the solution of a differential equation for a varying potential
is not just a smooth sequence of solutions for constant potentials,
but it does suggest that the right wave function for the oscillator
potential might decay as
. But the simple harmonic oscillator
potential is less penetrable than a flat barrier, because its
height increases as x2 as the particle penetrates
to large x. It follows from the expression for alpha above
that for large x alpha itself increases linearly
in x. Of course, this is something of a hand waving argument,
the solution of a differential equation for a varying potential
is not just a smooth sequence of solutions for constant potentials,
but it does suggest that the right wave function for the oscillator
potential might decay as  . We write it
as
. We write it
as  , so that the probability distribution
is proportional to
, so that the probability distribution
is proportional to 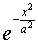 , and a, which
has the dimensions of length, is a natural measure of the spread
of the wave function.
, and a, which
has the dimensions of length, is a natural measure of the spread
of the wave function. 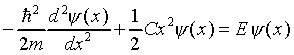
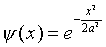 , it is straightforward to verify that
, it is straightforward to verify that
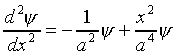


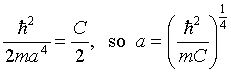 .
.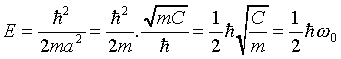 ,
,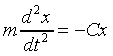 .
.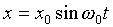 ,
, .
.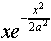 , and higher states have the x
replaced by a sequence of polynomials in x (called the
Hermite polynomials).
, and higher states have the x
replaced by a sequence of polynomials in x (called the
Hermite polynomials). 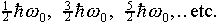 The simple harmonic oscillator is the only potential having uniformly
spaced energy levels.
The simple harmonic oscillator is the only potential having uniformly
spaced energy levels. 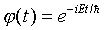 , and are states of definite energy E.
However, the full time dependent Schrödinger equation is
a linear equation, so if psi1(x,t)
and psi2(x,t) are solutions, so
is any linear combination Apsi1+Bpsi2.
Assuming psi1 and psi2 are
definite energy solutions for different energies E1
and E2, the combination will not correspond
to a definite energy-a measurement of the energy will give either
E1 or E2, with appropriate
probabilities. In the jargon, the combination is not an "eigenstate"
of the energy-but it is still a perfectly good, physically realizable
wave function.
, and are states of definite energy E.
However, the full time dependent Schrödinger equation is
a linear equation, so if psi1(x,t)
and psi2(x,t) are solutions, so
is any linear combination Apsi1+Bpsi2.
Assuming psi1 and psi2 are
definite energy solutions for different energies E1
and E2, the combination will not correspond
to a definite energy-a measurement of the energy will give either
E1 or E2, with appropriate
probabilities. In the jargon, the combination is not an "eigenstate"
of the energy-but it is still a perfectly good, physically realizable
wave function. 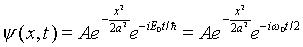
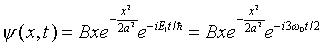 .
. .
.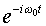 ,
so after time pi/omega_zero has elapsed, a factor
of -1 has evolved between the terms. If we now look at
the probability distribution |psi|2, it will
be skewed to the left. In other words, if the state is not of
definite energy, the probability distribution can vary in time.
Of course, the total probability of finding the particle
somewhere stays the same. Note that the probability distribution
swings back and forth with the period of the oscillator. This
discussion also implies that an ordinary pendulum, which clearly
swings back and forth, cannot be in a state of definite energy!
,
so after time pi/omega_zero has elapsed, a factor
of -1 has evolved between the terms. If we now look at
the probability distribution |psi|2, it will
be skewed to the left. In other words, if the state is not of
definite energy, the probability distribution can vary in time.
Of course, the total probability of finding the particle
somewhere stays the same. Note that the probability distribution
swings back and forth with the period of the oscillator. This
discussion also implies that an ordinary pendulum, which clearly
swings back and forth, cannot be in a state of definite energy!
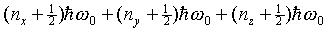 . For example, the lowest energy
state of the three dimensional harmonic oscillator, the zero point
energy, is
. For example, the lowest energy
state of the three dimensional harmonic oscillator, the zero point
energy, is 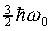 . Obviously, the higher energy
states are very degenerate-many sets of quantum numbers correspond
to the same state-because the energy only depends on the sum
of the three integer quantum numbers. Note that this degeneracy
arises from the symmetry of the potential, the spring constant
k is the same in all three directions. If the potential
were of the form ½k1x2
+ ½k2y2 + ½k3z2,
for general k's, there would be no degeneracy. (Such potentials
approximately describe oscillations of an atom in an anisotropic
crystal.)
. Obviously, the higher energy
states are very degenerate-many sets of quantum numbers correspond
to the same state-because the energy only depends on the sum
of the three integer quantum numbers. Note that this degeneracy
arises from the symmetry of the potential, the spring constant
k is the same in all three directions. If the potential
were of the form ½k1x2
+ ½k2y2 + ½k3z2,
for general k's, there would be no degeneracy. (Such potentials
approximately describe oscillations of an atom in an anisotropic
crystal.) .
.