Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
Daniel Bernoulli, in 1738, was the first to understand air pressure from a molecular point of view. He drew a picture of a vertical cylinder, closed at the bottom, with a piston at the top, the piston having a weight on it, both piston and weight being supported by the air pressure inside the cylinder. He described what went on inside the cylinder as follows: "let the cavity contain very minute corpuscles, which are driven hither and thither with a very rapid motion; so that these corpuscles, when they strike against the piston and sustain it by their repeated impacts, form an elastic fluid which will expand of itself if the weight is removed or diminished…" Sad to report, his insight, although essentially correct, was not widely accepted. Most scientists believed that the molecules in a gas stayed more or less in place, repelling each other from a distance, held somehow in the ether. Newton had shown that PV = constant followed if the repulsion was inverse-square. In fact, in the 1820's an Englishman, John Herapath, derived the relationship between pressure and molecular speed given below, and tried to get it published by the Royal Society. It was rejected by the president, Humphry Davy, who pointed out that equating temperature with motion, as Herapath did, implied that there would be an absolute zero of temperature, an idea Davy was reluctant to accept.
It is not difficult to extend Bernoulli's picture to a quantitative
description, relating the gas pressure to the molecular velocities. As
a warm up exercise, let us consider a single perfectly elastic particle,
of mass m, bouncing rapidly back and forth at speed v inside
a narrow cylinder of length L with a piston at one end, so all motion
is along the same line. What is the force on the piston?
Obviously, the piston doesn't feel a smooth continuous force, but a
series of equally spaced impacts. However, if the piston is much heavier
than the particle, this will have the same effect as a smooth force over
times long compared with the interval between impacts. So what is the value
of the equivalent smooth force?
Using Newton's law in the form force = rate of change of momentum,
we see that the particle's momentum changes by 2mv each time it
hits the piston. The time between hits is 2L/v, so the frequency
of hits is v/2L per second. This means that if there were
no balancing force, by conservation of momentum the particle would cause
the momentum of the piston to change by 2mv.v/2L units
in each second. This is the rate of change of momentum, and so must be
equal to the balancing force, which is therefore
F = mv2/L
We now generalize to the case of many particles bouncing around inside a rectangular box, of length L in the x-direction (which is along an edge of the box). The total force on the side of area A perpendicular to the x-direction is just a sum of single particle terms, the relevant velocity being the component of the velocity in the x-direction. The pressure is just the force per unit area, P = F/A. Of course, we don't know what the velocities of the particles are in an actual gas, but it turns out that we don't need the details. If we sum N contributions, one from each particle in the box, each contribution proportional to vx2 for that particle, the sum just gives us N times the average value of vx2. That is to say,
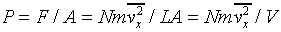
where there are N particles in a box of volume V. Next we note that the particles are equally likely to be moving in any direction, so the average value of vx2 must be the same at that of vy2 or vz2, and since v2 = vx2 + vy2 + vz2, it follows that
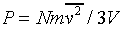
This is a surprisingly simple result! The macroscopic pressure of a
gas relates directly to the average kinetic energy per molecule. Of course,
in the above we have not thought about possible complications caused by
interactions between particles, but in fact for gases like air at room
temperature these interactions are very small. Furthermore, it is well
established experimentally that most gases satisfy the gas law over a wide
temperature range:
PV = nRT
for n moles of gas, that is, n = N/NA,
with NA Avogadro's number and R the gas constant.
Introducing Boltzmann's constant k = R/NA,
it is easy to check from our result for the pressure and the ideal gas
law that the average molecular kinetic energy is proportional to the
absolute temperature,
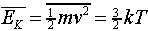 .
.
Boltzmann's constant k = 1.38.10-23 joules/K.
By the 1850's, various difficulties with the existing theories of heat, such as the caloric theory, caused some rethinking, and people took another look at the kinetic theory of Bernoulli, but little real progress was made until Maxwell attacked the problem in 1859. Maxwell worked with Bernoulli's picture, that the atoms or molecules in a gas were perfectly elastic particles, obeying Newton's laws, bouncing off each other (and the sides of the container) with straight line trajectories in between collisions. (Actually, there is some inelasticity in the collisions with the sides -- the bouncing molecule can excite or deexcite vibrations in the wall, this is how the gas and container come to thermal equilibrium.) Maxwell realized that it was completely hopeless to try to analyze this system using Newton's laws, even though it could be done in principle, there were far too many variables to begin writing down equations. On the other hand, a completely detailed description of how each molecule moved was not really needed anyway. What was needed was some understanding of how this microscopic picture connected with the macroscopic properties, which represented averages over huge numbers of molecules.
The relevant microscopic information is not knowledge of the
position and velocity of every molecule at every instant of time, but just
the distribution function, that is to say, what percentage of the
molecules are in a certain part of the container, and what percentage have
velocities within a certain range, at each instant of time. For a gas in
thermal equilibrium, the distribution function is independent of
time. Ignoring tiny corrections for gravity, the gas will be distributed
uniformly in the container, so the only unknown is the velocity
distribution function.
Maxwell found the velocity distribution function for gas molecules in
thermal equilibrium by the following elegant argument based on symmetry.
For a gas of N particles, let the number of particles having velocity in the x-direction between vx and vx + dvx be Nf(vx)dvx. In other words, f(vx)dvx is the fraction of all the particles having x-direction velocity lying in the interval between vx and vx + dvx.
But there's nothing special about the x-direction -- for gas
molecules in a container, at least away from the walls, all directions
look the same, so the same function f will give the probability
distributions in the other directions too, the probability for the velocity
to lie between vx and vx + dvx,
vy and vy + dvy, and
vz and vz + dvz will
be:
Nf(vx)dvxf(vy)dvyf(vz)dvz = Nf(vx) f(vy) f(vz) dvxdvydvz.
Note that this distribution function, when integrated over all possible
values of the three components of velocity, gives the total number of particles
to be N, as it should.
Next comes the clever part - since any direction is as good as any other
direction, the distribution function must depend only on the total
speed of the particle, not on the separate velocity components.
Therefore, Maxwell argues, it must be that:
f(vx) f(vy)
f(vz) = F(vx2
+ vy2 + vz2)
where F is another unknown function. However, it is apparent
that the product of the functions on the left is reflected in the
sum of variables on the right. It will only come out that way if
the variables appear in an exponent in the functions on the left. In
fact, it is easy to check that this equation is solved by a function of
the form:
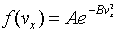
Here A and B are arbitrary constants. Following Maxwell, we have put a minus sign in the exponent because there must eventually be fewer and fewer particles as we go to higher speeds, certainly not a diverging number. Multiplying together the probability distributions for the three directions gives the distribution in terms of particle speed v. However, in this case the natural distribution function is that giving the number of particles having speed between v and v + dv.
It is important to think about the distribution of particles in velocity
space, a three-dimensional space (vx, vy,
vz), where each particle is represented by a point having
coordinates corresponding to the particle's velocity. Thus, all points
lying on a spherical surface centered at the origin correspond to the same
speed. Therefore, the number of particles having speed between v
and v + dv equals the number of points lying between two
spheres centered at the origin, with radii v and v + dv.
This is the space that replaces the little box dvxdvydvz.
The volume of the spherical shell is 4.pi.v2dv.
Therefore, the probability distribution as a function of speed is:
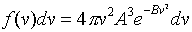
The constants A and B can be determined by integrating
this probability distribution over all possible speeds to find the total
number of particles N, and their total energy E.
Since a particle moving at speed v has kinetic energy ½mv2,
we can use the probability distribution to find the average kinetic energy
per particle:
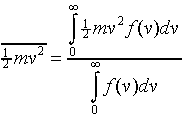
The numerator is the total energy, the denominator is the total number
of particles. Notice that the unknown constant A cancels between
numerator and denominator. Substituting the value of f(v)
in the integrals, we find
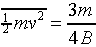 .
.
Substituting the value for the average kinetic energy in terms of the temperature of the gas,
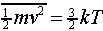
we find B = m/2kT, so
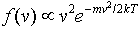
The constant of proportionality is given by integrating over all speeds
and setting the result equal to one (since we factored out the number of
particles N in our definition of f(v).)
The final result is:
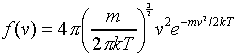
(This function is called g in Tipler.)
Note that this function increases parabolically from zero for low speeds,
reaches a maximum, then decreases exponentially. As the temperature increases,
the position of the maximum shifts to the right. The total area under the
curve is always one, by definition. For air molecules (say, nitrogen) at
room temperature the curve is:
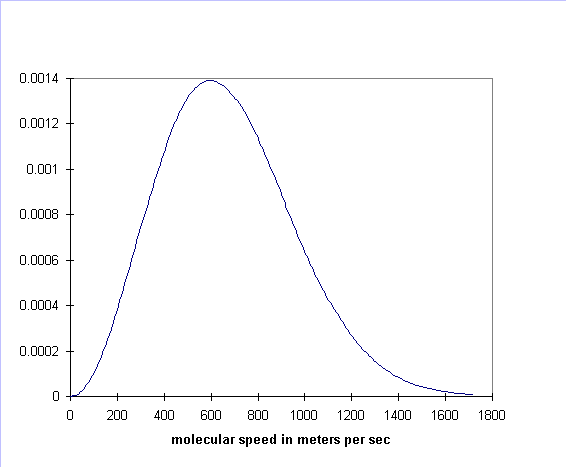
There are two key features of the Maxwell distribution for an ideal gas that we wish to emphasize:
1. There is on average an energy ½kT in each degree of freedom
2. The probability of a molecule having energy E is proportional to e-E/kT.
By a "degree of freedom" we mean a way in which a molecule if free to move, and thus have energy - in this case, just the x, y, and z directions, to give total average kinetic energy 3.½kT.
Boltzmann generalized these features of Maxwell's distribution to arbitrary large systems. He was the first to realize the deep connection between the thermodynamic concept of entropy and the statistical analysis of possible states of a large system - that the increase in entropy of a system with time is a change in macroscopic variables to those values corresponding to the largest possible number of microscopic arrangements. He showed that the numbers of available microscopic states for a given energy are far greater for macroscopic values corresponding to thermal equilibrium. For example, for a given energy there are far more possible microscopic arrangements of gas molecules in which the gas is essentially uniformly distributed in a box than there are corresponding to all the gas molecules being in the left-hand half of the box. Thus, if a liter of gas over the course of time goes through all possible microscopic arrangements, in fact there is a negligible probability of it all being in the left-hand half in a time the age of the universe. So if we arrange for all the particles to be in the left-hand half by using a piston to push them there, then remove the piston, they will rapidly tend to a uniform distribution spread evenly throughout the box.
Boltzmann proved that the thermodynamic entropy S of a system (at a given energy E, say) was related to the number W of microscopic states available to it by S = klogW, k being Boltzmann's constant. (There were some ambiguities in counting the number of possible microscopic arrangements which were rather troublesome, but not fatal to the program. For example, how many different velocities can a particle in a box have? We shall see later in the course that these problems were cleared up by quantum mechanics.)
He was then able to establish that for any system large or small in thermal equilibrium at temperature T, the probability of being in a particular state at energy E is proportional to e-E/kT. This is called the Boltzmann distribution.
Historical Note: Boltzmann's analysis of entropy in terms of underlying microscopic configurations was ridiculed by some very powerful figures in the German scientific establishment, led by the famous chemist W. Ostwald, who did not believe in atoms! Boltzmann was depressed by these attacks and by his own poor health, and took his own life in 1906. Ostwald got the Nobel prize in 1909. He died in 1932, and never believed in atoms (at least, that's the impression given by the article in the Encyclopedia Britannica).
To return to Maxwell's analysis of the gas in the box, we have stated
that the total average kinetic energy per molecule is 1.5kT at temperature
T, so the specific heat per molecule is presumable 1.5k,
and given that k = R/NA, the specific heat
per mole comes out at 1.5R. In fact, this is experimentally confirmed
for monatomic gases. However, it is found that diatomic gases can have
specific heats of 2.5R and even 3.5R. This is not difficult
to understand - these molecules have more degrees of freedom. A dumbbell
molecule can rotate about two directions perpendicular to its axis. A diatomic
molecule could also vibrate. Such a simple harmonic oscillator motion has
both kinetic and potential energy, and it turns out to have total energy
kT in thermal equilibrium. Thus, reasonable explanations for the
specific heats of various gases can be concocted by assuming a contribution
½k from each degree of freedom. But there are problems. Why
shouldn't the dumbbell rotate about its axis? Why do monatomic atoms not
rotate at all? Even more ominously, the specific heat of hydrogen, 2.5R
at room temperature, drops to 1.5R at lower temperatures. These
problems were not resolved until the advent of quantum mechanics.
Physics 252 Home Page
Link to Next Lecture
An applet of Bernoulli's picture, which may take a while to retrieve, but is quite good, can be found here.
Copyright ©1997 Michael Fowler