Michael Fowler
University of Virginia
Physics 252 Home PageWe shall now turn to another puzzle confronting physicists at the turn of the century -- just how heated bodies radiate. There was a general understanding of the mechanism involved -- heat was known to cause the molecules and atoms of a solid to vibrate, and it was known that the molecules and atoms were themselves complicated patterns of electrical charges. From the experiments of Hertz and others Maxwell's predictions that oscillating charges emitted electromagnetic radiation had been confirmed, at least for simple antennas. It was known from Maxwell's equations that this radiation traveled at the speed of light and from this it was realized that light itself, and the closely related infrared heat radiation, were actually electromagnetic waves. The picture, then, was that when a body was heated, the consequent vibrations on a molecular and atomic scale included some oscillating charges. If one assumed that Maxwell's theory of electromagnetic radiation, which worked well in the macroscopic world, was also valid at the microscopic scale (tenths of nanometers), then these oscillating charges would radiate, presumably giving off heat and light.
What is meant by the phrase "black body" radiation? The point
is that radiation from heated bodies depends to some extent on the body
heated. Let us back up momentarily and consider how differently different
materials absorb radiation. Some, like glass, seem to absorb light
hardly at all-the light goes through. For a shiny metallic surface, the
light isn't absorbed either, it gets reflected. For a black material like
soot, light and heat are almost completely absorbed, and the material gets
warm. How can we understand these different behaviors in terms of light
as an electromagnetic wave interacting with charges in the material, causing
them to oscillate and absorb energy from the radiation? In the case of
glass, evidently this doesn't happen, at least not much. A full understanding
of how this works needs quantum mechanics, but the general idea is as follows.
There are charges-electrons-in glass that are able to oscillate in response
to an applied external oscillating electric field, but these charges are
tightly bound to atoms, and only oscillate at certain frequencies. It happens
that for ordinary glass none of these frequencies correspond to those of
visible light, so there is no resonance with a light wave, and hence little
energy absorbed. Glass is opaque at some frequencies outside the visible
range (in general, both in the infrared and the ultraviolet). These are
the frequencies at which the electrical charge distribution in the atoms
or bonds can naturally oscillate.
A piece of metal has electrons free to move through the entire solid.
This is why metals can conduct electricity. It is also why they are shiny.
These unattached electrons oscillate together with large amplitude in response
to the electrical field of an incoming light wave. They themselves then
radiate electromagnetically, just like a current in an antenna. This radiation
from the oscillating electrons is the reflected light. In this situation,
little of the incoming radiant energy is absorbed, it is just reradiated,
that is, reflected.
Soot, like a metal, will conduct an electric current, although not nearly so well. There are unattached electrons, which can move through the whole solid, but they keep bumping into things-they have a short mean free path. When they bump, they cause vibration, like a pinball machine, so they give up energy into heat. Although the electrons in soot have a short mean free path compared to that in a good metal, they move very freely compared with electrons in atoms, so they can accelerate and pick up energy from the electric field in the light wave. They are therefore effective intermediaries in transferring energy from the light wave into heat.
Heated bodies radiate by processes just like the absorption described
above operating in reverse. Thus, for soot heat causes the lattice to vibrate
more vigorously, giving energy to the electrons (imagine them as balls
in a pinball machine with strongly vibrating barriers, etc.) and since
the electrons are charged they radiate away excess kinetic energy. On the
other hand, the electrons in a metal have very long mean free paths, the
lattice vibrations affect them much less, so they are less effective in
radiating away heat. It is evident from considerations like this that good
absorbers of radiation are also good emitters.
At sufficiently high temperatures, all bodies become good radiators. Items heated until they glow in a fire look much more similar than they do at room temperature. For a metal, this can be understood in terms of a shortening of the mean free path by the stronger vibrations of the lattice interfering with the electron's passage.
Any body at any temperature above absolute zero will radiate to some
extent, but the intensity and frequency distribution of the radiation depends
on the detailed structure of the body. To make any progress in understanding
radiation, we must specify the details of the body radiating. The simplest
possible model is to consider a body which is a perfect absorber, and therefore
the best possible emitter. For obvious reasons, this is called a "black
body".
A good model absorber is a small hole in the side of a box. Radiation
impinging on the hole from outside enters the box and is absorbed as it
is scattered around inside, so only a tiny fraction is re-emitted.
We shall, therefore, take a cubical box (an oven, in other words) with
a small hole in the side as our model to analyze emission of radiation.
Fortunately, this is a system which can also be investigated experimentally
fairly easily. A beam of radiation from the hole in the oven is passed
through a diffraction grating and projected on to a screen, where it is
separated out by wavelength (or equivalently frequency). A detector is
moved up and down along the screen to find how much radiant energy is being
emitted in each frequency range, say the energy between frequency f
and f + df is RT(f)df.
We can then plot RT(f) against f for
a given temperature T. It is found experimentally that for small
f, RT(f) is proportional to f2,
a parabolic shape, but for increasing f it falls below the parabola,
peaks at fmax, then falls quite rapidly to zero as f
increases beyond fmax.
Suppose we now double the absolute temperature - how does that affect
RT(f)?
For those low frequencies where RT(f) was parabolic,
doubling the temperature doubles the intensity of the radiation. However,
it is found that at 2T the curve follows the (doubled) parabolic
path much further - in fact, twice as far: fmax(2T)
= 2fmax(T).
The curve R2T(f), then, reaches eight times
the height of RT(f). It also spreads over twice
the lateral extent, so the area under the curve, corresponding to the total
energy radiated, increases sixteenfold on doubling the temperature.
This is Stefan's Law of Radiation: the power P radiated from one
square meter of black surface at temperature T:
Note that the graph above plots the energy intensity in the oven. This
energy is being pumped out of the opening at speed c. When allowance
is made for the fact that an opening of unit area is effectively less than
unit area for radiation coming in at an angle, and half the energy is in
waves moving in directions away from the whole, the actual rate of emission
of energy through a hole of unit area is equal to (1/4)c times the
energy intensity inside.
The upward shift in fmax with T is something
everyone is familiar with - when an iron is heated in a fire, the first
visible radiation is deep red - the lowest frequency visible light. Further
increase in T causes the color to change to orange then yellow,
and white at a very high temperature, signifying that all the visible frequencies
are being emitted roughly equally.
The change in fmax is linear in the absolute temperature;
This is called Wein's Displacement Law.
For example, the sun's surface temperature is 5700K, and at that temperature
much of the energy is radiated as visible light. This is no accident -
evolution has adapted us to see most efficiently in the light most readily
available.
This shift in the frequency at which radiant power is a maximum is very important for harnessing solar energy, such as in a greenhouse. We need glass which will allow the solar radiation in, but not let the heat radiation out. This is feasible because the two radiations are in very different frequency ranges - 5700K and, say, 300K - and there are materials transparent to light but opaque to infrared radiation. This is only possible because fmax varies with temperature.
Experimental investigations of the radiation intensity as a function
of temperature and frequency, RT(f) above, give
well-defined reproducible results, not very sensitive to the material of
the oven, etc. For a small hole, the radiation emitted will be a representative
sample of the radiation bouncing around inside the box.
In fact, the general shape of the function RT(f) was very reminiscent of the energy distribution in a gas in thermal equilibrium, as analyzed by Maxwell and Boltzmann. In contrast to the molecules in a gas, the different wavelengths of radiation do not collide with each other in the middle of the oven. Nevertheless, energy can shift from one mode to the other through the intermediary of the oscillators in the wall - which is to say, just the atoms and molecules the wall is made of. An electromagnetic wave in the oven can set a charge oscillating in the wall, energy can be transferred to other charges in the wall, which will in general oscillate and radiate at different frequencies. Thus the different frequencies of radiation inside the oven will come to thermal equilibrium.
To make any quantitative progress in analyzing the radiation, we must
have a clear picture of the degrees of freedom of this system - how many
oscillators have frequencies in a given energy range? These oscillations
are standing electromagnetic waves. The waves are contained in the oven,
so the electric field intensity drops rapidly to zero on approaching and
going into the walls, because inside the walls the electric energy will
be rapidly dissipated by currents or polarization. In fact, then, the boundary
condition at the walls is much like that for waves on a string fixed at
both ends, where the wave amplitude goes to zero at the ends.
As a warm up exercise, consider the frequency distribution function
of the possible different modes of vibration (that is, the different degrees
of freedom) of a string stretched between two points a distance a
apart. Possible values of the wavelength are:
so the frequency
The allowed frequencies are thus equally spaced c/2a apart.
We define the spectral density by stating that the number of modes between
f and f + delta_f is N(f)delta_f
for delta_f small compared with the range of frequencies in the
system, but large compared with the spacing between successive allowed
frequencies. Evidently, in this simple one-dimensional example N(f)
is a constant equal to 2a/c.
The amplitude of oscillation as a function of time has the form:
This is more conveniently written:
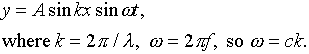
Here 
is the radial frequency
- how many radians per second, rather than cycles per second, the
time dependent component of the wave moves through. Analogously, k,
called the wave number, counts the radians of spatial change in
unit length (such as one meter).
We are now ready to tackle the more complex problem of three-dimensional standing electromagnetic waves in a cubical oven. The first guess, just generalizing the expression above, would be:
This will satisfy the wave equation
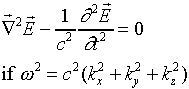
Also the electric field will be zero at all the walls if we choose the
k's appropriately, that is, so that sinkxa = 0,
etc.
However, this wave is not quite correct, because since there is no electric
charge in the oven away from the walls, the divergence of the electric
field must be identically zero away from the walls, a condition this wave
does not satisfy. The divergence is:
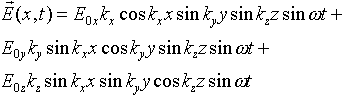
and, for example, taking any x for which sinkxx
= 0, the second and third terms above are identically zero, but the first
term certainly isn't.
This problem can be fixed by thinking more carefully about the boundary conditions at the walls. It is true that any component of the electric field parallel to the wall will be attenuated rapidly by currents or polarization in the wall. However, there could be an electric field perpendicular to the wall, because there could be surface charge on the wall. This means a possible solution is:
These components are deliberately chosen to give
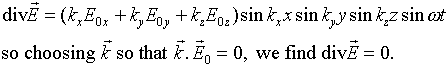
This is telling us something we should have realized from the beginning
- in the standing electromagnetic wave in the cavity, just as in a propagating
wave, the electric field is perpendicular to the direction in which the
wave is moving. In other words, it is a transverse wave, and in fact there
are two independent polarizations, which we must remember to count when
we find the total number of degrees of freedom.
It remains to find the allowed frequencies of vibration - the normal
modes - of the electromagnetic radiation in the oven. The first step is
to find the allowed values of the wave numbers kx, ky
and kz. These are fixed by the boundary conditions sinkxa
= 0, etc., so
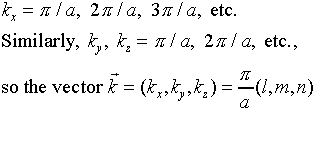
where( l, m, n) are positive integers, like (1,
1, 1) or (5, 13, 4) - in other words, each possible standing electromagnetic
wave in the oven corresponds to a point in the (kx, ky,
kz) space labeled by three positive integers. These are
the intersection points of a cubic lattice in the space kx
> 0, ky > 0, kz > 0.
Each such point can be associated with the little lattice cube of volume
for which the point in question
is the furthest corner of the little cube from the k-space origin.
These little cubes stack together to fill all that part of k-space
having kx > 0, ky > 0 and kz
> 0.
The frequency of vibration of the wave having wave numbers (kx,
ky, kz) is
Recall that the experimental measurement of black body radiation from
the oven detects the intensity of radiation in a given frequency
range. It does not tell us the wave numbers of the radiating modes!
Hence, to compare with these experimental results, we must choose a small
frequency range and find how many possible sets of wave numbers correspond
to modes of vibration having frequencies within that range.
Notice that a fixed value of the frequency corresponds to a spherical
surface in k-space:
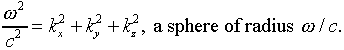
Therefore, the number of possible modes of radiation in the oven having
frequencies in the range 
is
equal to the number of lattice-point wave number values (kx,
ky, kz) between two spherical surfaces
centered at the origin and having radii 
,
and only counting in the octant corresponding to kx >
0, ky > 0 and kz > 0.
Now, as we argues above, each lattice point can be associated with a
small cube of volume 
. Assuming
we choose 
, there will be many
of these small cubes between the spherical surfaces, and the total number
of lattice points between the spheres in the positive octant will be just
the volume of the space between the spheres divided by the volume of one
of these cubes.
So the number of possible modes of radiation in the oven having frequencies
in the range 
is:
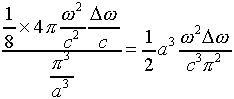
Putting this in terms of the frequency f in cycles per second,
, and inserting an extra factor
of two for the two independent polarizations of the wave (discussed above)
we find the distribution function for modes in frequency is given by:
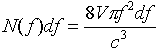
where V = a3 is the volume of the oven.
The point of the rather tedious calculation above, finding exactly how
many different modes of vibration, or degrees of freedom, there are in
the ovenfull of radiation, was to construct an argument parallel to that
applied successfully to understand the properties of gases. The first conclusion
would be that there is kT of energy, on average in each wave mode
(not ½kT, because the standing wave is like an oscillator
with both kinetic and potential energy).
For low frequencies, this is exactly what is observed. The amount of radiation shining out of the oven at low frequencies is correctly predicted by counting modes, as above, and allocating kT of energy to each mode.
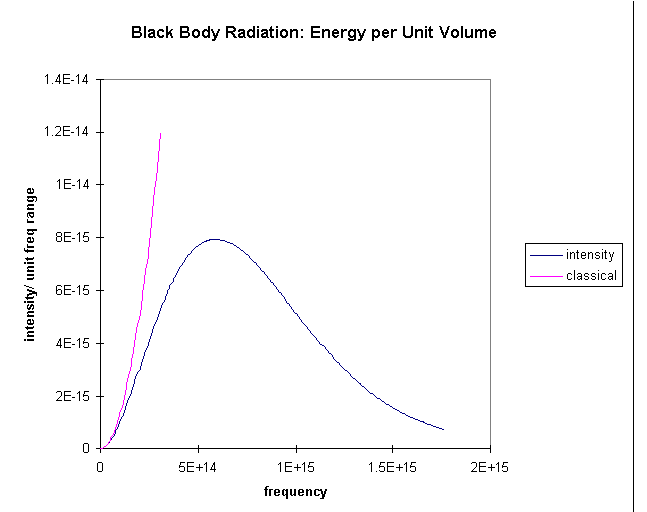
The problem is that as we go to higher frequencies, there are more and
more possible degrees of freedom. The oven should be radiating huge amounts
of energy in the blue and ultraviolet. But it isn't. For this system, the
equipartition of energy isn't working!
The graph shows the prediction of radiation intensity from the classical
equipartition compared with the experimental result. It is evident that
the higher frequency modes are not getting their "fair share"
kT of energy, somehow they are getting frozen out, evidently those
at really high frequencies are getting almost no share in the energy at
all.
It is important at this point to go back to the curves earlier in this
lecture for two different temperatures, and ask the question: how
is the sharing of energy among the modes affected by raising the temperature?
We provide below a magnified version of the low frequency parts of the
curves for T/2 and T, and show for each case the classical
prediction based on the mode counting in the preceding section. Look at
the curves and think about this before reading on!
It is clear that for the lowest frequencies, doubling the temperature does indeed double the intensity of the radiation, exactly what we expect if the radiation is proportional to kT, the energy in each mode. (T = 300K here, by the way.) We can also see, though, that at the higher temperature, the observed radiation intensity stays closer to the classical prediction as we go to higher frequencies. This means the higher modes are less locked out of the energy sharing when we go to higher temperatures. For any given temperature, though, if we go to high enough frequencies, the intensity drops exponentially with further increase in frequency.
Planck suggested that this lack of equipartition could be understood
if the oscillators in the walls of the oven were somehow constrained so
that they could not continuously emit radiation, as Maxwell's equations
would predict, but could only emit it in chunks - called quanta
- of a definite magnitude. For higher frequencies, he suggested, the radiation
had to be emitted in bigger chunks. This would explain the lack of radiation
in the oven at these higher frequencies - assuming the oscillators in the
walls had on average energy kT, it would be very unlikely that one
oscillating charge would by random excitation have an energy of, say, 5kT,
so if its frequency of oscillation were high enough, it would almost never
have enough energy to emit one quantum, so by Planck's theory, it wouldn't
emit any radiation at all. On the other hand, if the temperature were increased
fivefold, it would often have enough energy to emit a quantum.
Given, then, that bigger chunks of energy are emitted at the higher
frequencies, just how does the size of a chunk depend on the frequency
of the radiation? The clue is given by the Wein displacement formula, 
.
Now, fmax is the frequency at which the curve turns over
and begins to descend, moving far from the classically predicted parabola,
which of course continues upwards. Thus, doubling the temperature doubles
the frequency range over which the curve approximates the classically predicted
parabola. (If we stiffen the requirements for approximating the classical
curve, for example by requiring it to be within 5%, say, then we can see
from the graph of low energy modes above that doubling the temperature
still doubles the range over which the curves remain close.)
The bottom line is that doubling the temperature apparently doubles
the frequency range in which oscillators get approximately their full share
kT of energy. But doubling the temperature doubles the size of a
chunk of energy that can be easily moved. This leads to the conclusion
that if two oscillators have frequencies f and 2f, the one
at 2f must emit energy in quanta just twice the size of those emitted
by the one at f. The size of the energy quantum therefore depends
linearly on the frequency,
E = hf
where h is Planck's constant.
The way this evolved historically was that at first the higher frequency
part of the black body radiation curve was mapped out by experimentalists
in Berlin, and Wien showed that it was well approximated by the formula
with A a constant. This was very reminiscent of the Maxwell distribution
for gas molecules, but with f3 in place of v2.
It soon became evident, though, that the formula was not accurate at low
frequencies, where in fact it appeared that the distribution went as f2,
as discussed above. Planck then wrote down a formula having the right behavior
for both high and low frequencies:
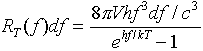
He did not at first have any theoretical justification for this formula, but it was a very accurate fit to some very precise experiments.
It is easy to see how Wien's Displacement Law follows from this formula --- the maximum radiation per unit frequency range is at the frequency f for which the function f3/(ehf/kT-1) is a maximum. Solving numerically gives hfmax=2.82kT. (It is perhaps worth mentioning that this is the frequency range at which the radiation per unit frequency range is a maximum. In some older books, Wien's law is written in terms of wavelengths, and gives the wavelength at which the radiation per unit wavelength range is maximum. Because the wavelength and frequency are not linearly related, but in fact inversely related, these two maxima are not at the same frequency!)
Factoring out the number of modes of oscillation in the frequency range
df, we see that Planck's formula tells us that the average energy per mode
is
For low frequencies, hf << kT, this correctly gives kT per mode. The formula follows if we assume the oscillator can only have a whole number of quanta of energy, that is to say, its energy must be one of: 0, hf, 2hf, 3hf, … If we further assume that the relative probability of it having energy E is e-E/kT, then its relative probabilities of having energy 0, hf, 2hf, … are in the ratio 1: e-hf/kT : e-2hf/kT, etc. The actual probabilities are given by dividing these relative probabilities by the sum of all of them They clearly are the terms of a geometric series, so their sum is just 1/(1 - e-hf/kT). So, to find the average energy in the oscillator, we take the possible energies 0, hf, 2hf, 3hf, … and weight each of them with their probability of occurring, that is, we must find 0.1 + hf. e-hf/kT +2hf. e-2hf/kT + … , and divide the sum by 1/(1 - e-hf/kT). This is left as an exercise for the reader. Planck himself gave a more complete and elegant discussion, applying Boltzmann's ideas about entropy to simple harmonic oscillators having only certain energies allowed. In fact, he effectively derived the Boltzmann distribution for this system.
Copyright Michael Fowler ©1997