Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
The most dramatic prediction of Maxwell's theory of electromagnetism,
published in 1865, was the existence of electromagnetic waves moving at
the speed of light, and the conclusion that light itself was just such
a wave. This challenged experimentalists to generate and detect electromagnetic
radiation using some form of electrical apparatus. The first clearly successful
attempt was by Heinrich Hertz in 1886. He used a high voltage induction
coil to cause a spark discharge between two pieces of brass, to quote him,
"Imagine a cylindrical brass body, 3 cm in diameter and 26 cm long,
interrupted midway along its length by a spark gap whose poles on either
side are formed by spheres of 2 cm radius." The idea was that
once a spark formed a conducting path between the two brass conductors,
charge would rapidly oscillate back and forth, emitting electromagnetic
radiation of a wavelength similar to the size of the conductors themselves.
To prove there really was radiation emitted, it had to be detected.
Hertz used a piece of copper wire 1 mm thick bent into a circle of diameter
7.5 cms, with a small brass sphere on one end, and the other end of the
wire was pointed, with the point near the sphere. He added a screw mechanism
so that the point could be moved very close to the sphere in a controlled
fashion. This "receiver" was designed so that current oscillating
back and forth in the wire would have a natural period close to that of
the "transmitter" described above. The presence of oscillating
charge in the receiver would be signaled by a spark across the (tiny) gap
between the point and the sphere (typically, this gap was hundredths of
a millimeter). (It was suggested to Hertz that this spark gap could be
replaced as a detector by a suitably prepared frog's leg, but that apparently
didn't work.)
The experiment was very successful - Hertz was able to detect the radiation
up to fifty feet away, and in a series of ingenious experiments established
that the radiation was reflected and refracted as expected, and that it
was polarized. The main problem - the limiting factor in detection -- was
being able to see the tiny spark in the receiver. In trying to improve
the spark's visibility, he came upon something very mysterious. To quote
from Hertz again (he called the transmitter spark A, the receiver
B): "I occasionally enclosed the spark B in a dark case
so as to more easily make the observations; and in so doing I observed
that the maximum spark-length became decidedly smaller in the case than
it was before. On removing in succession the various parts of the case,
it was seen that the only portion of it which exercised this prejudicial
effect was that which screened the spark B from the spark A. The partition
on that side exhibited this effect, not only when it was in the immediate
neighbourhood of the spark B, but also when it was interposed at greater
distances from B between A and B. A phenomenon so remarkable called for
closer investigation."
Hertz then embarked on a very thorough investigation. He found that
the small receiver spark was more vigorous if it was exposed to ultraviolet
light from the transmitter spark. It took a long time to figure this out
- he first checked for some kind of electromagnetic effect, but found a
sheet of glass effectively shielded the spark. He then found a slab of
quartz did not shield the spark, whereupon he used a quartz prism to break
up the light from the big spark into its components, and discovered that
the wavelength which made the little spark more powerful was beyond the
visible, in the ultraviolet.
In 1887, Hertz concluded what must have been months of investigation: "… I confine myself at present to communicating the results obtained, without attempting any theory respecting the manner in which the observed phenomena are brought about."
The next year, 1888, another German physicist, Wilhelm Hallwachs, in Dresden, wrote:
"In a recent publication Hertz has described investigations
on the dependence of the maximum length of an induction spark on the radiation
received by it from another induction spark. He proved that the phenomenon
observed is an action of the ultraviolet light. No further light on the
nature of the phenomenon could be obtained, because of the complicated
conditions of the research in which it appeared. I have endeavored to obtain
related phenomena which would occur under simpler conditions, in order
to make the explanation of the phenomena easier. Success was obtained by
investigating the action of the electric light on electrically charged
bodies."
He then describes his very simple experiment: a clean circular plate
of zinc was mounted on an insulating stand and attached by a wire to a
gold leaf electroscope, which was then charged negatively. The electroscope
lost its charge very slowly. However, if the zinc plate was exposed to
ultraviolet light from an arc lamp, or from burning magnesium, charge leaked
away quickly. If the plate was positively charged, there was no fast charge
leakage. (We showed this as a lecture demo, using a UV lamp as source.)
Questions for the reader: Could it be that the ultraviolet light
somehow spoiled the insulating properties of the stand the zinc plate was
on? Could it be that electric or magnetic effects from the large current
in the arc lamp somehow caused the charge leakage?
Although Hallwach's experiment certainly clarified the situation, he did not offer any theory of what was going on.
In fact, the situation remained unclear until 1899, when Thomson established
that the ultraviolet light caused electrons to be emitted, the same
particles found in cathode rays. His method was to enclose the metallic
surface to be exposed to radiation in a vacuum tube, in other words to
make it the cathode in a cathode ray tube. The new feature was that electrons
were to be ejected from the cathode by the radiation, rather than by the
strong electric field used previously.
By this time, there was a plausible picture of what was going on. Atoms in the cathode contained electrons, which were shaken and caused to vibrate by the oscillating electric field of the incident radiation. Eventually some of them would be shaken loose, and would be ejected from the cathode. It is worthwhile considering carefully how the number and speed of electrons emitted would be expected to vary with the intensity and color of the incident radiation. Increasing the intensity of radiation would shake the electrons more violently, so one would expect more to be emitted, and they would shoot out at greater speed, on average. Increasing the frequency of the radiation would shake the electrons faster, so might cause the electrons to come out faster. For very dim light, it would take some time for an electron to work up to a sufficient amplitude of vibration to shake loose.
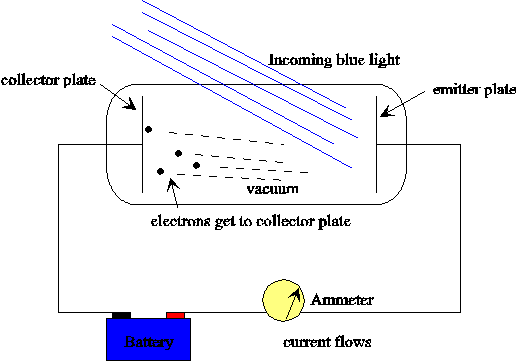
In 1902, Lenard studied how the energy of the emitted photoelectrons varied with the intensity of the light. He used a carbon arc light, and could increase the intensity a thousand-fold. The ejected electrons hit another metal plate, the collector, which was connected to the cathode by a wire with a sensitive ammeter, to measure the current produced by the illumination. To measure the energy of the ejected electrons, Lenard charged the collector plate negatively, to repel the electrons coming towards it. Thus, only electrons ejected with enough kinetic energy to get up this potential hill would contribute to the current. Lenard discovered that there was a well defined minimum voltage that stopped any electrons getting through, we'll call it Vstop. To his surprise, he found that Vstop did not depend at all on the intensity of the light! Doubling the light intensity doubled the number of electrons emitted, but did not affect the energies of the emitted electrons. The more powerful oscillating field ejected more electrons, but the maximum individual energy of the ejected electrons was the same as for the weaker field.
But Lenard did something else. With his very powerful arc lamp, there was sufficient intensity to separate out the colors and check the photoelectric effect using light of different colors. He found that the maximum energy of the ejected electrons did depend on the color --- the shorter wavelength, higher frequency light caused electrons to be ejected with more energy. This was, however, a fairly qualitative conclusion --- the energy measurements were not very reproducible, because they were extremely sensitive to the condition of the surface, in particular its state of partial oxidation. In the best vacua available at that time, significant oxidation of a fresh surface took place in tens of minutes. (The details of the surface are crucial because the fastest electrons emitted are those from right at the surface, and their binding to the solid depends strongly on the nature of the surface --- is it pure metal or a mixture of metal and oxygen atoms?)

Question: In the above figure, the battery represents the potential Lenard used to charge the collector plate negatively, which would actually be a variable voltage source. Since the electrons ejected by the blue light are getting to the collector plate, evidently the potential supplied by the battery is less than Vstop for blue light. Show with an arrow on the wire the direction of the electric current in the wire.
In 1905 Einstein gave a very simple interpretation of Lenard's results.
He just assumed that the incoming radiation should be thought of as quanta
of frequency hf, with f the frequency. In photoemission,
one such quantum is absorbed by one electron. If the electron is some distance
into the material of the cathode, some energy will be lost as it moves
towards the surface. There will always be some electrostatic cost as the
electron leaves the surface, this is usually called the work function,
W. The most energetic electrons emitted will be those very close
to the surface, and they will leave the cathode with kinetic energy
E = hf - W.
On cranking up the negative voltage on the collector plate until the
current just stops, that is, to Vstop, the highest kinetic
energy electrons must have had energy eVstop on leaving
the cathode. Thus,
eVstop = hf - W
Thus Einstein's theory makes a very definite quantitative prediction:
if the frequency of the incident light is varied, and Vstop
plotted as a function of frequency, the slope of the line should be h/e.
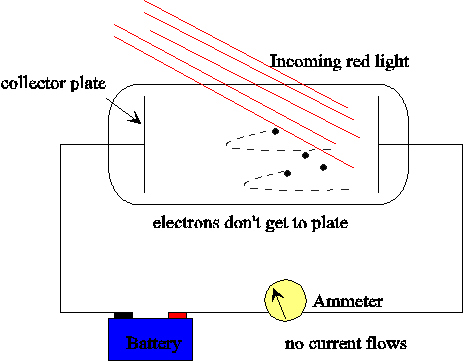
It is also clear that there is a minimum light frequency for a given metal, that for which the quantum of energy is equal to the work function. Light below that frequency , no matter how bright, will not cause photoemission.
If we accept Einstein's theory, then, this is a completely different
way to measure Planck's constant. The American experimental physicist
Robert
Millikan, who did not accept Einstein's theory, which he saw as an attack
on the wave theory of light, worked for ten years, until 1916, on the photoelectric
effect. He even devised techniques for scraping clean the metal surfaces
inside the vacuum tube. For all his efforts he found disappointing results:
he confirmed Einstein's theory, measuring Planck's constant to within 0.5%
by this method. One consolation was that he did get a Nobel prize for this
series of experiments.
'Subtle is the Lord...' The Science and Life of Albert Einstein, Abraham Pais, Oxford 1982.
Inward Bound, Abraham Pais, Oxford, 1986
The Project Physics Course, Text, Holt, Rinehart, Winston, 1970
Physics 252 Home Page
Link to Next Lecture
Copyright ©1997 Michael Fowler