How Relativity Connects Electric and Magnetic Fields
Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
Suppose we have an infinitely long straight wire, having a charge
density of electrons of 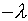 coulombs per
meter, all moving at speed v to the right (recall typical
speeds are centimeters per minute) and a neutralizing fixed background
of positive charge,
coulombs per
meter, all moving at speed v to the right (recall typical
speeds are centimeters per minute) and a neutralizing fixed background
of positive charge, 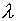 coulombs per meter.
The current I in the wire has magnitude
coulombs per meter.
The current I in the wire has magnitude 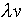 (and actually is flowing to the left). Suppose now a positive
charge q outside the wire, a distance r from the
axis, is also moving at speed v. (Of course, both positive
and negative charges are distributed uniformly throughout the
wire. We just show them separated for ease of visualization.)
(and actually is flowing to the left). Suppose now a positive
charge q outside the wire, a distance r from the
axis, is also moving at speed v. (Of course, both positive
and negative charges are distributed uniformly throughout the
wire. We just show them separated for ease of visualization.)
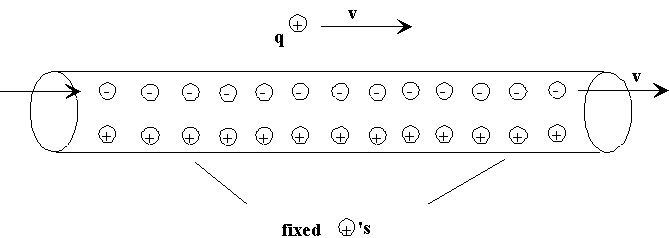
What force does q feel?
The magnetic field strength is 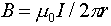 (from
(from
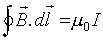 ), and
), and 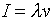 , so
, so
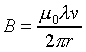
The magnetic force F on q is 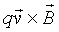 ,
pointing directly away from the wire, and of magnitude
,
pointing directly away from the wire, and of magnitude
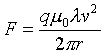 .
.
Therefore, if the initial situation is as in the figure above,
the charge will accelerate away from the wire.
Let us now examine the same physical system in the frame of reference
in which the charge is initially at rest. In this frame, the electrons
are also at rest, but the positive background charge is flowing
at -v as shown.
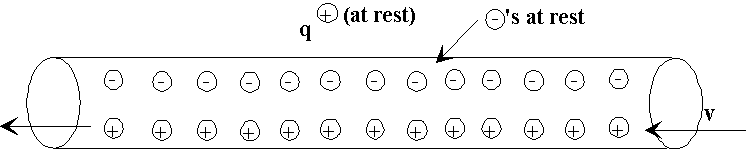
What force does q feel in this frame? Since q is
at rest, it cannot feel a magnetic force, since such forces
depend linearly on speed.
Yet it looks as if it can't feel an electric force either, because
of the equal densities of positive and negative charges in the
wire. So, we might conclude that in this frame q feels
no force at all, so will not move. But we just proved that in
the other frame, q accelerates away from the wire! These
statements can't both be right-if q moves away from the
wire in one frame, it must in the other (recall also these frames
are moving relative to each other at centimeters per minute).
The mistake in the above argument is that we neglected Fitzgerald-Lorentz
contraction. If we (correctly) assume that in the frame where
the wire is at rest, the positive and negative charge densities
exactly cancel, they will no longer do so in the frame where we
take the external charge at rest and the wire moving. In this
frame, the positive charges are moving at v, so since their charge
density was 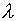 at rest, in this frame it
must be
at rest, in this frame it
must be 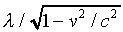 . Since v is extremely
small, we can take the extra density to be
. Since v is extremely
small, we can take the extra density to be  .
.
Similarly, the electrons are at rest in this frame, so their density
is less by 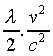 .
.
These two effects do not cancel, but add, to give in this frame
a positive electrostatic charge density equal to 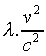 .
Using
.
Using 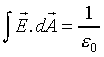 (enclosed charge), we find an electrostatic
outward field of magnitude
(enclosed charge), we find an electrostatic
outward field of magnitude  . This electrostatic
field exerts a force on the charge q of magnitude
. This electrostatic
field exerts a force on the charge q of magnitude
 .
.
But 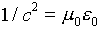 , so this electrostatic force is identical
in magnitude to the magnetic force we found in the other frame!
So observers in the two frames will agree on the rate at which
the particle accelerates away from the wire, but one will call
it a magnetic force, the other an electric force. We must conclude
that whether a particular force on an actual particle is magnetic
or electric depends on the frame of reference-so the distinction
is rather artificial.
, so this electrostatic force is identical
in magnitude to the magnetic force we found in the other frame!
So observers in the two frames will agree on the rate at which
the particle accelerates away from the wire, but one will call
it a magnetic force, the other an electric force. We must conclude
that whether a particular force on an actual particle is magnetic
or electric depends on the frame of reference-so the distinction
is rather artificial.
Physics 252 Home Page
Link to Next Lecture
Copyright © 1996 Michael Fowler
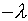 coulombs per
meter, all moving at speed v to the right (recall typical
speeds are centimeters per minute) and a neutralizing fixed background
of positive charge,
coulombs per
meter, all moving at speed v to the right (recall typical
speeds are centimeters per minute) and a neutralizing fixed background
of positive charge, 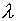 coulombs per meter.
The current I in the wire has magnitude
coulombs per meter.
The current I in the wire has magnitude 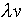 (and actually is flowing to the left). Suppose now a positive
charge q outside the wire, a distance r from the
axis, is also moving at speed v. (Of course, both positive
and negative charges are distributed uniformly throughout the
wire. We just show them separated for ease of visualization.)
(and actually is flowing to the left). Suppose now a positive
charge q outside the wire, a distance r from the
axis, is also moving at speed v. (Of course, both positive
and negative charges are distributed uniformly throughout the
wire. We just show them separated for ease of visualization.)

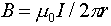 (from
(from
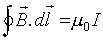 ), and
), and 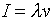 , so
, so
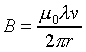
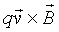 ,
pointing directly away from the wire, and of magnitude
,
pointing directly away from the wire, and of magnitude
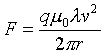 .
.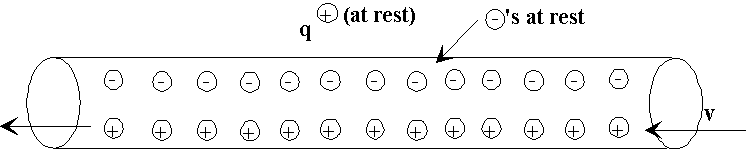
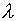 at rest, in this frame it
must be
at rest, in this frame it
must be 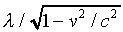 . Since v is extremely
small, we can take the extra density to be
. Since v is extremely
small, we can take the extra density to be  .
.
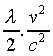 .
.
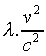 .
Using
.
Using 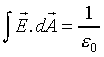 (enclosed charge), we find an electrostatic
outward field of magnitude
(enclosed charge), we find an electrostatic
outward field of magnitude  . This electrostatic
field exerts a force on the charge q of magnitude
. This electrostatic
field exerts a force on the charge q of magnitude
 .
.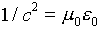 , so this electrostatic force is identical
in magnitude to the magnetic force we found in the other frame!
So observers in the two frames will agree on the rate at which
the particle accelerates away from the wire, but one will call
it a magnetic force, the other an electric force. We must conclude
that whether a particular force on an actual particle is magnetic
or electric depends on the frame of reference-so the distinction
is rather artificial.
, so this electrostatic force is identical
in magnitude to the magnetic force we found in the other frame!
So observers in the two frames will agree on the rate at which
the particle accelerates away from the wire, but one will call
it a magnetic force, the other an electric force. We must conclude
that whether a particular force on an actual particle is magnetic
or electric depends on the frame of reference-so the distinction
is rather artificial.