Transforming Energy into Mass: Particle Creation
Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
We have mentioned how, using a synchrocyclotron, it is possible to accelerate
protons to relativistic speeds. The rest energy of a proton mpc2
is 938 MeV, using here the standard high energy physics energy unit: 1
MeV = 106 eV. The neutron is a bit heavier -- mnc2
= 940 MeV. (The electron is 0.51 MeV). Thus to accelerate a proton to relativistic
speeds implies giving it a K.E. of order 1,000 MeV, or 1 GeV.
The standard operating procedure of high energy physicists is to accelerate
particles to relativistic speeds, then smash them into other particles
to see what happens. For example, fast protons will be aimed at protons
at rest (hydrogen atoms, in other words -- the electron can be neglected).
These proton-proton collisions take place inside some kind of detection
apparatus, so the results can be observed. One widely used detector is
the bubble chamber: a transparent container filled with a superheated liquid.
The electric field of a rapidly moving charged particle passing close to
a molecule can dislodge an electron, so an energetic particle moving through
the liquid leaves a trail of ionized molecules. These give centers about
bubbles can nucleate. The bubbles grow rapidly and provide a visible record
of the particle's path.
What is actually observed in p-p scattering at relativistic
energies is that often more particles come out than went in-particles called
pions, 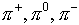 can be created. The
can be created. The 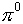 is
electrically neutral, the
is
electrically neutral, the  has exactly
the same amount of charge as the proton. It is found experimentally that
total electric charge is always conserved in collisions, no matter how
many new particles are spawned, and total baryon number (protons + neutrons)
is conserved.
has exactly
the same amount of charge as the proton. It is found experimentally that
total electric charge is always conserved in collisions, no matter how
many new particles are spawned, and total baryon number (protons + neutrons)
is conserved.
Possible scenarios include:
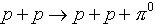
and
 .
.
The neutral pion mass is 135 MeV, the charged pions have mass 140 MeV,
where we follow standard high energy practice in calling mc2
the "mass", since this is the energy equivalent, and hence the
energy which, on creation of the particle in a collision, is taken from
kinetic energy and stored in mass.
However, an incoming proton with 135 MeV of kinetic energy will not
be able to create a neutral pion in a collision with a stationary proton.
This is because the incoming proton also has momentum, and the collision
conserves momentum, so some of the particles after the collision must have
momentum and hence kinetic energy. The simplest way to figure out just
how much energy the incoming proton needs to create a neutral pion is to
go to the center of mass frame, where initially two protons are moving
towards each other with equal and opposite velocities, there is no total
momentum. Obviously, in this frame the least possible K.E. must be just
enough to create the 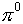 with all the final
state particles
with all the final
state particles 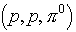 at rest. Thus if the relativistic
mass of the incoming protons in the center of mass frame is m, the
total energy
at rest. Thus if the relativistic
mass of the incoming protons in the center of mass frame is m, the
total energy
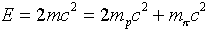
Putting in the proton and pion masses from above, and using m
= mp /sqrt (1 - v2/c2),
we find the two incoming protons must both be traveling at 0.36c.
Recall that this is the speed in the center of mass frame, and for practical
purposes, like designing the accelerator, we need to know the energy necessary
in the "lab" frame-that in which one of the protons is initially
at rest. The two frames obviously have a relative speed of 0.36c,
so to get the speed of the incoming proton in the lab frame we must add
a velocity of 0.36c to one of 0.36c using the relativistic
addition of velocities formula, which gives 0.64c. This implies
the incoming proton has a relativistic mass of 1.3 times its rest mass,
and thus a K.E. around 280 MeV.
Thus to create a pion of rest energy 135 MeV, it is necessary to give
the incoming proton at least 280 MeV of kinetic energy. This is called
the "threshold energy" for pion production. The "inefficiency"
arises because momentum is also conserved, so there is still considerable
K.E. in the final particles.
Antiproton Production
On raising the energy of the incoming proton further, more particles
are produced, including the "antiproton" -- a negatively charged
heavy particle which will annihilate a proton in a flash of energy. It
turns out experimentally that an antiproton can only be produced accompanied
by a newly created proton,
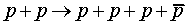
Notice we could have conserved electric charge with less energy with
the reaction
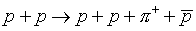
but this doesn't happen -- so charge conservation isn't the only constraint
on what particles can be produced. In fact, what we are seeing here is
experimental confirmation that the conservation of baryon number, which
at the low energies previously discussed in the context of pion production
just meant that the total number of protons plus neutrons stayed fixed,
is generalized at high energies to include antiparticles with negative
baryon number, -1 for the antiproton. Thus baryon number conservation becomes
parallel to electric charge conservation, new particles can always be produced
at high enough energies provided the total new charge and the total new
baryon number are both zero. (Actually there are further conservation laws
which become important when more exotic particles are produced, which we
may discuss later.) We should emphasize again that these are experimental
results gathered from examining millions of collisions between relativistic
particles.
One of the first modern accelerators, built at Berkeley in the fifties,
was designed specifically to produce the antiproton, so it was very important
to calculate the antiproton production threshold correctly! This can be
done by the same method we used above for pion production, but we use a
different trick here which is often useful. We have shown that on transforming
the energy and momentum of a particle from one frame to another

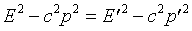
Since the Lorentz equations are linear, if we have a system of particles
with total energy E and total momentum p in one frame, E',
p' in another, it must again be true that
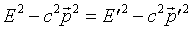
We can use this invariance to get lab frame information from the center
of mass frame. Noting that in the center of mass (cm) frame the momentum
is zero, and in the lab frame the momentum is all in the incoming proton,
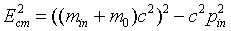
where here m0 is the proton rest mass, min
is the relativistic mass of the incoming proton. At the antiproton production
threshold, Ecm = 4m0c2,
so
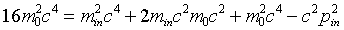
and using
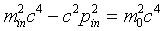
we find
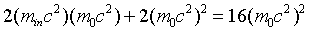 ,
,
so
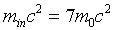 .
.
Therefore to create two extra particles, with total rest energy 2m0c2,
it is necessary for the incoming proton to have a kinetic energy of 6m0c2.
The Berkeley Gevatron had design energy 6.2 GeV.
As we go to higher energies, this "inefficiency" gets worse-consider
energies such that the kinetic energy >> rest energy, and assume
the incoming particle and the target particle have the same rest mass,
m0, with the incoming particle having relativistic mass
m.
CM: O ---> <--- O pCM = 0.
LAB: O -----> O pLAB = mv.
..........m.......... m0
ELAB = (m + m0)c2.
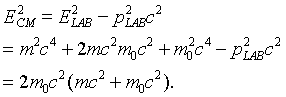
For m >> m0,
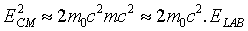
so
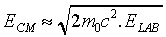 .
.
Physics 252 Home Page
Link to Next Lecture
Copyright ©1997 Michael Fowler
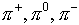 can be created. The
can be created. The 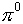 is
electrically neutral, the
is
electrically neutral, the  has exactly
the same amount of charge as the proton. It is found experimentally that
total electric charge is always conserved in collisions, no matter how
many new particles are spawned, and total baryon number (protons + neutrons)
is conserved.
has exactly
the same amount of charge as the proton. It is found experimentally that
total electric charge is always conserved in collisions, no matter how
many new particles are spawned, and total baryon number (protons + neutrons)
is conserved. 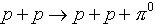
 .
.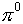 with all the final
state particles
with all the final
state particles 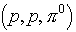 at rest. Thus if the relativistic
mass of the incoming protons in the center of mass frame is m, the
total energy
at rest. Thus if the relativistic
mass of the incoming protons in the center of mass frame is m, the
total energy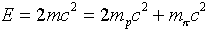
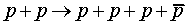
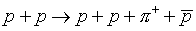

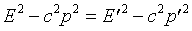
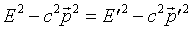
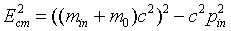
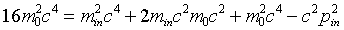
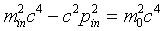
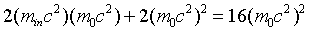 ,
,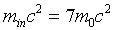 .
.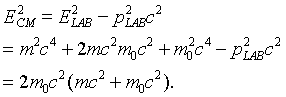
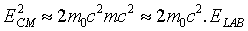
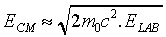 .
.