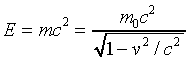
Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
We have a formula for the total energy E = K.E. + rest energy,
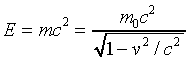
so we can see how total energy varies with speed.
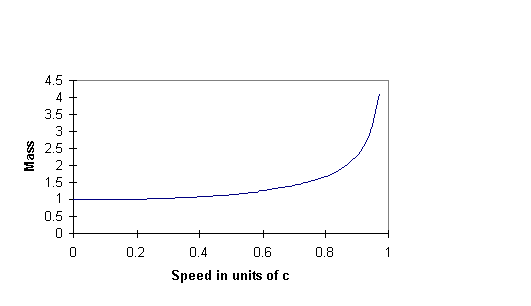
The momentum varies with speed as
.
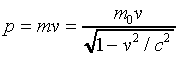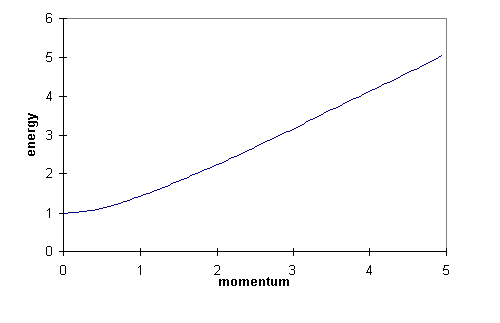
It turns out to be useful to have a formula for E in terms
of p.
Now
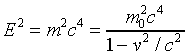
so
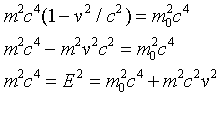
hence using p = mv we find
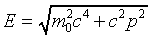.If p is very small, this gives
,
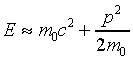the usual classical formula.
If p is very large, so c2p2 >> m02c4, the approximate formula is E = cp.
Notice that this high energy limit is just the energy-momentum relationship Maxwell found to be true for light, for all p. This could only be true for all p if m02c4 = 0, that is, m0 = 0. Light is in fact composed of "photons"-particles having zero "rest mass", as we shall discuss later. The "rest mass" of a photon is meaningless, since they're never at rest-the energy of a photon
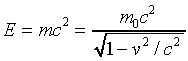
is of the form 0/0, since m0 = 0 and v
= c, so "m" can still be nonzero. That
is to say, the mass of a photon is really all K.E. mass.
For very fast electrons, such as those produced in high energy
accelerators, the additional K.E. mass can be thousands of times
the rest mass. For these particles, we can neglect the rest mass
and take E = cp.
We have shown
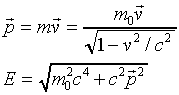
Notice we can write this last equation in the form
.
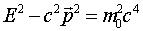That is to say,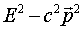 
depends only on the rest
mass of the particle and the speed of light. It does not depend
on the velocity of the particle, so it must be the same-for a
particular particle-in all inertial frames. This is reminiscent
of the invariance of 
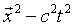, the interval squared
between two events, under the Lorentz transformations. One might
guess from this that the laws governing the transformation from
E, p in one Lorentz frame to E', p'
in another are similar to those for x,t. We can
actually derive the laws for E,p to check this out.
As usual, we consider all velocities to be parallel to the x-axis.
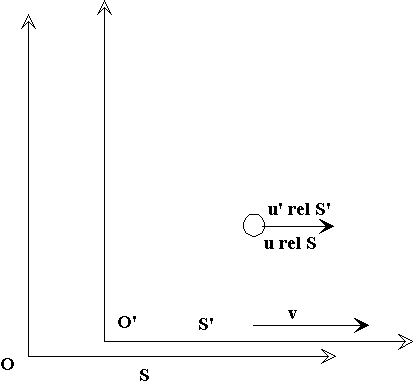
We take the frame S' to be moving in the x-direction at
speed v relative to S.
Consider a particle of mass m0 (rest mass) moving at u' in the x' direction in frame S', and hence at u along x in S, where
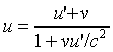.The energy and momentum in S' are
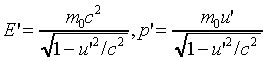
and in S:
.
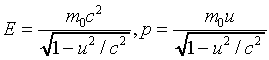Thus
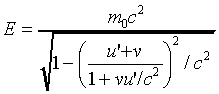
giving
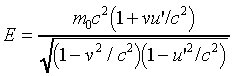
from which it is easy to show that
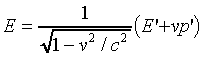.Similarly we can show that
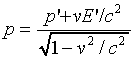.These are the Lorentz transformations for energy and momentum of a particle -- it is easy to check that
.
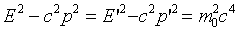NOTE the special case of a zero rest mass particle: E =
cp, E2 - c2p2
= 0 in all frames.
Thus
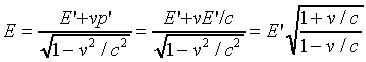.Since E = cp, E' = cp' we also have
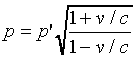.Notice that the ratios of energies in the two frames coincides with the ratio of frequencies found in the Doppler shift.
Physics 252 Home Page
Link to Next Lecture
Copyright ©1997 Michael Fowler