 .
.Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture.
The fact that feeding energy into a body increases its mass suggests
that the mass m0 of a body at rest, multiplied
by c2, can be considered as a quantity of energy.
The truth of this is best seen in interactions between elementary
particles. For example, there is a particle called a positron
which is exactly like an electron except that it has positive
charge. If a positron and an electron collide at low speed (so
there is very little kinetic energy) they both disappear in a
flash of electromagnetic radiation. This can be detected and its
energy measured. It turns out to be 2m0c2
where m0 is the mass of the electron (and the
positron).
Thus particles can "vaporize" into pure energy, that is, electromagnetic radiation. The energy m0c2 of a particle at rest is called its "rest energy". Note, however, that an electron can only be vaporized by meeting with a positron, and there are very few positrons around normally, for obvious reasons-they just don't get far. (Although occasionally it has been suggested that some galaxies may be antimatter!)
An amusing "experiment" on the equivalence of mass and
energy is the following: consider a closed box with a flashlight
at one end and light-absorbing material at the other end. Imagine
the box to be far out in space away from gravitational fields
or any disturbances. Suppose the light flashes once, the flash
travels down the box and is absorbed at the other end.
Now it is known from Maxwell's theory of electromagnetic waves
that a flash of light carrying energy E also carries momentum
p = E/c. Thus, as the flash leaves the bulb
and goes down the tube, the box recoils, like a gun, to conserve
overall momentum. Suppose the whole apparatus has mass M
and recoils at velocity v. Of course, v <<
c.
Then from conservation of momentum:
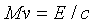 .
.
After a time t = L/C the light hits the far
end of the tube, is absorbed, and the whole thing comes to rest
again. (We are assuming that the distance moved by the box is
tiny compared to its length.)
How far did the box move?
It moved at speed v for time t, so it moved distance
vt = vL/c.
From the conservation of momentum equation above, we see that v = E/Mc, so the distance d the box moved over before stopping is given by:
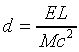 .
.
Now, the important thing is that there are no external
forces acting on this system, so the center of mass cannot
have moved!
The only way this makes sense is to say that to counterbalance the mass M moving d backwards, the light energy must have transferred a small mass m, say, the length L of the tube so that
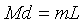
and balance is maintained. From our formula for d above, we can figure out the necessary value of m,
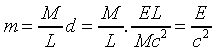
so
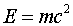 .
.
We have therefore established that transfer of energy implies
transfer of the equivalent mass. All we had to assume was
that the center of mass of an isolated system, initially at rest,
remains at test if no external forces act, and that electromagnetic
radiation carries momentum E/c, as predicted by
Maxwell's equations and experimentally established.
But how is this mass transfer physically realized? Is the front end of the tube really heavier after it absorbs the light? The answer is yes, because it's a bit hotter, which means its atoms are vibrating slightly faster -- and faster moving objects have higher mass.
Suppose now at the far end of the tube we have a hydrogen atom
at rest. As we shall discuss later, this can be thought of as
a proton with an electron bound to it by electrostatic attraction,
and it is known that a flash of light having total energy 13.6eV
is just enough to tear the electron away, so in the end the proton
and electron are at rest far away from each other. The energy
of the light was used up dragging the proton and electron apart
-- that is, it went into potential energy. Yet the light is
absorbed by this process, so from our argument above the right
hand end of the tube must become heavier. That is to say,
a proton at rest plus a (distant) electron at rest weigh more
than a hydrogen atom by E/c2, with
E equal to 13.6eV. Thus, Einstein's box forces us to conclude
that increased potential energy in a system also entails
the appropriate increase in mass.
It is interesting to consider the hydrogen atom dissociation in
reverse -- if a slow moving electron encounters an isolated proton,
they may combine to form a hydrogen atom, emitting 13.6eV of electromagnetic
radiation energy as they do so. Clearly, then, the hydrogen atom
remaining has that much less energy than the initial proton +
electron. The actual mass difference for hydrogen atoms is about
one part in 108. This is typical of the energy radiated
away in a violent chemical reaction -- in fact, since most atoms
are an order of magnitude or more heavier than hydrogen, a part
in 109 or 1010 is more usual. However, things
are very different in nuclear physics, where the forces are stronger
so the binding is tighter. We shall discuss this later, but briefly
mention an example-a hydrogen nucleus can combine with a lithium
nucleus to give two helium nuclei, and the mass shed is 1/500
of the original. This reaction has been observed, and all the
masses involved are measurable. The actual energy emitted is 17
MeV. This is the type of reaction that occurs in hydrogen bombs.
Notice that the energy released is at least a million times more
than the most violent chemical reaction.
Final example -- give a ballpark estimate of the change in mass of a million tons of TNT on exploding. The TNT molecule is about a hundred times heavier than the hydrogen atom, and gives off a few eV on burning. So the change in weight is of order 10-10 x106 tons, about a hundred grams. In a hydrogen bomb, this same mass to energy conversion would take about fifty kilograms of fuel.
Although Einstein's box argument is easy to understand, and gives the correct result, it is based on a physical fiction -- the rigid box. If we had a rigid box, or even a rigid stick, all our clock synchronization problems would be over -- we could start clocks at the two ends of the stick simultaneously by nudging the stick from one end, and, since it's a rigid stick, the other end would move instantaneously. Actually there are no such materials. All materials are held together by electromagnetic forces, and pushing one end causes a wave of compression to travel down the stick. The electrical forces between atoms adjust at the speed of light, but the overall wave travels far more slowly because each atom in the chain must accelerate for a while before it moves sufficiently to affect the next one measurably. So the light pulse will reach the other end of the box before it has begun to move! Nevertheless, the wobbling elastic box does have a net recoil momentum, which it does lose when the light hits the far end. So the basic point is still valid. French gives a legitimate derivation by replacing the box by its two (disconnected) ends, which he treats as a single system.
Physics 252 Home Page
Link to Next Lecture.
Copyright ©1997 Michael Fowler