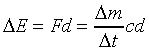
Michael Fowler
UVa Physics
Physics 252 Home Page
Link to Previous Lecture
The first coherent statement of what physicists now call relativity
was Galileo's observation almost four hundred years ago that if
you were in a large closed room, you could not tell by observing
how things move-living things, thrown things, dripping liquids-whether
the room was at rest in a building, say, or below decks in a large
ship moving with a steady velocity. More technically (but really
saying the same thing!) we would put it that the laws of motion
are the same in any inertial frame. That is, these laws really
only describe relative positions and velocities. In particular,
they do not single out a special inertial frame as the one that's
"really at rest". This was later all written down more
formally, in terms of Galilean transformations. Using these
simple linear equations, motion analyzed in terms of positions
and velocities in one inertial frame could be translated into
any other. When, after Galileo, Newton wrote down his Three Laws
of Motion, they were of course invariant under the Galilean transformations,
and valid in any inertial frame.
About two hundred years ago, it became clear that light was not
just a stream of particles (as Newton had thought) but manifested
definite wavelike properties. This led naturally to the
question of what, exactly, was waving, and the consensus was that
space was filled with an aether, and light waves were ripples
in this all-pervading aether analogous to sound waves in air.
Maxwell's discovery that the equations describing electromagnetic
phenomena had wavelike solutions, and predicted a speed which
coincided with the measured speed of light, suggested that electric
and magnetic fields were stresses or strains in the aether, and
Maxwell's equations were presumably only precisely correct in
the frame in which the aether was at rest. However, very precise
experiments which should have been able to detect this aether
all failed.
Almost one hundred years ago, Einstein suggested that maybe all
the laws of physics were the same in all inertial frames,
generalizing Galileo's pronouncements concerning motion to include
the more recently discovered laws of electricity and magnetism.
This would imply there could be no special "really at rest"
frame, even for light propagation, and hence no aether. This is
a very appealing and very simple concept: the same laws apply
in all frames. What could be more reasonable? As we have seen,
though, it turns out to clash with some beliefs about space and
time deeply held by everybody encountering this for the first
time. The central prediction is that since the speed of light
follows from the laws of physics (Maxwell's equations) and some
simple electrostatic and magnetostatic experiments, which are
clearly frame-independent, the speed of light is the same in
all inertial frames. That is to say, the speed of a particular
flash of light will always be measured to be 3 108
meters per second even if measured by different observers moving
rapidly relative to each other, where each observer measures the
speed of the flash relative to himself. Nevertheless, experiments
have show again and again that Einstein's elegant insight is right,
and everybody's deeply held beliefs are wrong.
We have discussed in detail the kinematical consequences of Einstein's postulate-how measurements of position, time and velocity in one frame relate to those in another, and how apparent paradoxes can be resolved by careful analysis. So far, though, we have not thought much about dynamics. We know that Newton's Laws of Motion were invariant under the Galilean transformations between inertial frames. We now know that the Galilean transformations are in fact incorrect except in the low speed nonrelativistic limit. Therefore, we had better look carefully at Newton's Laws of Motion in light of our new knowledge.
Newton's First Law, the Principle of Inertia, that an object subject
to no external forces will continue to move in a straight line
at steady speed, is equally valid in special relativity. Indeed,
it is the defining property of an inertial frame that this is
true, and the content of special relativity is transformations
between such frames.
Newton's Second Law, stated in the form force = mass x acceleration,
cannot be true as it stands in special relativity. This is evident
from the formula we derived for addition of velocities. Think
of a rocket having many stages, each sufficient to boost the remainder
of the rocket (including the unused stages) to c/2 from
rest. We could fire them one after the other in a carefully timed
way to generate a continuous large force on the rocket, which
would get it to c/2 in the first firing. If the acceleration
continued, the rocket would very soon be exceeding the speed of
light. Yet we know from the addition of velocities formula that
in fact the rocket never reaches c. Evidently, Newton's
Second Law needs updating.
Newton's Third Law, action = reaction, also has problems. Consider some attractive force between two rapidly moving bodies. As their distance apart varies, so does the force of attraction. We might be tempted to say that the force of A on B is the opposite of the force of B on A, at each instant of time, but that implies simultaneous measurements at two bodies some distance from each other, and if it happens to be true in A's inertial frame, it won't be in B's.
In nonrelativistic Newtonian physics, the Third Law tells us that
two interacting bodies feel equal but opposite forces from the
interaction. Therefore from the Second Law, the rate of change
of momentum of one of the bodies is equal and opposite to that
of the other body, thus the total rate of change of momentum
of the system caused by the interaction is zero. Consequently,
for any closed dynamical system (no outside forces acting)
the total momentum never changes. This is the law
of conservation of momentum. It does not depend on
the details of the forces of interaction between the bodies, only
that they be equal and opposite.
The other major dynamical conservation law is the conservation
of energy. This was not fully formulated until long after Newton,
when it became clear that frictional heat generation, for example,
could quantitatively account for the apparent loss of kinetic
plus potential energy in actual dynamical systems.
Although these conservation laws were originally formulated within a Newtonian worldview, their very general nature suggested to Einstein that they might have a wider validity. Therefore, as a working hypothesis, he assumed them to be satisfied in all inertial frames, and explored the consequences. We follow that approach.
As a warm-up exercise, let us consider conservation of momentum for a collision of two balls on a pool table. We draw a chalk line down the middle of the pool table, and shoot the balls close to, but on opposite sides of, the chalk line from either end, at the same speed, so they will hit in the middle with a glancing blow, which will turn their velocities through a small angle. In other words, if initially we say their (equal magnitude, opposite direction) velocities were parallel to the x-direction -- the chalk line -- then after the collision they will also have equal and opposite small velocities in the y-direction. (The x-direction velocities will have decreased very slightly).
Now let us repeat the exercise on a grand scale. Suppose somewhere
in space, far from any gravitational fields, we set out a string
one million miles long. (It could be between our two clocks in
the time dilation experiment). This string corresponds to the
chalk line on the pool table. Suppose now we have two identical
spaceships approaching each other with equal and opposite velocities
parallel to the string from the two ends of the string, aimed
so that they suffer a slight glancing collision when they meet
in the middle. It is evident from the symmetry of the situation
that momentum is conserved in both directions. In particular,
the rate at which one spaceship moves away from the string after
the collision - its y-velocity - is equal and opposite
to the rate at which the other one moves away from the string.
But now consider this collision as observed by someone in one of the spaceships, call it A. (Remember, momentum must be conserved in all inertial frames -- they are all equivalent -- there is nothing special about the frame in which the string is at rest.) Before the collision, he sees the string moving very fast by the window, say a few meters away. After the collision, he sees the string to be moving away, at, say, 15 meters per second. This is because spaceship A has picked up a velocity perpendicular to the string of 15 meters per second. Meanwhile, since this is a completely symmetrical situation, an observer on spaceship B would certainly deduce that her spaceship was moving away from the string at 15 meters per second as well.
The crucial question is: how fast does an observer in spaceship
A see spaceship B to be moving away from the string? Let us
suppose that relative to spaceship A, spaceship B
is moving away (in the x-direction) at 0.6c. First,
recall that distances perpendicular to the direction of motion
are not Lorentz contracted. Therefore, when the observer in spaceship
B says she has moved 15 meters further away from the string
in a one second interval, the observer watching this movement
from spaceship A will agree on the 15 meters - but disagree
on the one second! He will say her clocks run slow, so as measured
by his clocks 1.25 seconds will have elapsed as she moves 15 meters
in the y-direction.
It follows that, as a result of time dilation, this collision as viewed from spaceship A does not cause equal and opposite velocities for the two spaceships in the y-direction. Initially, both spaceships were moving parallel to the x-axis - there was zero momentum in the y-direction. Consider y-direction momentum conservation in the inertial frame in which A was initially at rest. An observer in that frame measuring y-velocities after the collision will find A to be moving at 15 meters per second, B to be moving at -0.8 x 15 meters per second in the y-direction. So how can we argue there is zero total momentum in the y-direction after the collision, when the identical spaceships do not have equal and opposite velocities?
Einstein was so sure that momentum conservation must always hold
that he rescued it with a bold hypothesis: the mass of an object
must depend on its speed! In fact, the mass must increase with
speed in just such a way as to cancel out the lower y-direction
velocity resulting from time dilation. That is to say, if an object
at rest has a mass M, moving at a speed v it will
have a mass M/sqrt(1 - v²/c²).
Note that this is an undetectably small effect at ordinary speeds,
but as an object approaches the speed of light, the mass increases
without limit!
Of course, we have taken a very special case here - a particular kind of collision. The reader might well wonder if the same mass correction would work in other types of collision, for example a straight line collision in which a heavy object rear-ends a lighter object. The algebra is straightforward, if tedious, and it is found that this mass correction factor does indeed ensure momentum conservation for any collision in all inertial frames.
Deciding that masses of objects must depend on speed like this
seems a heavy price to pay to rescue conservation of momentum!
However, it is a prediction that is not difficult to check by
experiment. The first confirmation came in 1908, measuring the
mass of fast electrons in a vacuum tube. In fact, the electrons
in a color TV tube are about half a percent heavier than electrons
at rest, and this must be allowed for in calculating the magnetic
fields used to guide them to the screen.
Much more dramatically, in modern particle accelerators very powerful electric fields are used to accelerate electrons, protons and other particles. It is found in practice that these particles become heavier and heavier as the speed of light is approached, and hence need greater and greater forces for further acceleration. Consequently, the speed of light is a natural absolute speed limit. Particles are accelerated to speeds where their mass is thousands of times greater than their mass measured at rest, usually called the "rest mass".
As everyone has heard, in special relativity mass and energy are not separately conserved, in certain situations mass m can be converted to energy E = mc2. This equivalence is closely related to the mass increase with speed, as we shall see. In fact, French derives it by analyzing a collision and stipulating mass conservation in the collision, where mass is now the speed-dependent mass discussed above. Part of French's point in doing this is to demonstrate that it follows from very general considerations, for example concepts like force do not need to be introduced. We shall take a less sophisticated route below, in which we find the kinetic energy of an object as it is accelerated in a straight line by a force, such as the electric field acting on an electron in a linear accelerator, and assume Newton's second law is valid provided mass x acceleration is replaced by rate of change of momentum, a more general concept.
Let's first think about the kinetic energy of a particle traveling
close to the speed of light. If a force F acts on the particle
accelerating it in its direction of motion, and the particle moves
through a distance d in the direction the force is pushing,
the force does work Fd, and this must go into the kinetic
energy of the particle (assuming as always conservation of energy).
As a warm up, recall the elementary derivation of the kinetic
energy ½mv² of an ordinary non-relativistic
(i.e. slow moving) object of mass m. This can be done by
accelerating the mass with a constant force F, and finding
the work done by the force (force distance) to get it to speed
v from a standing start. The kinetic energy of the mass,
E = ½mv², equals the work done by the
force in bringing the mass up to that speed from rest: if it takes
time t, and the (uniform) acceleration is a, then
the final speed v = at, the average speed during acceleration
is ½v, so the distance traveled is ½vt,
the work done by the force is ½Fvt = ½mavt
= ½mv2. It is easy to extend this to show
that if the mass was initially moving as speed u, the work done
by the force is ½mv2 - ½mu2.
We are now ready to think about the change in kinetic energy of
a particle acted on by an accelerating force when the particle
is already moving practically at the speed of light, like particles
in modern accelerators. The most straightforward way to see what
happens is to use Newton's Second Law, which in the form
is still true, but close to the speed of light the speed changes
negligibly as the force continues to work-instead, the mass increases.
Therefore to an excellent approximation,
where as usual c is the speed of light.
To give a concrete example, let us imagine we have a particle
moving very close to the speed of light, and we apply an accelerating
force F as the particle travels in a straight line through
a distance d. (In a particle accelerator, for example,
the particle with charge q could enter a region of uniform
electric field E and feel a force F = qE.)
Then the increase in kinetic energy delta_E is given by
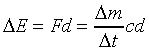
where we have approximated the rate of change of mass by the actual
change over the distance d, assumed small, divided by the
time taken to traverse d,
Substituting this value for delta_t in the formula for
the increase in kinetic energy delta_E, we find
Recall that to get momentum to be conserved in all inertial frames,
we had to assume an increase of mass with speed by the factor
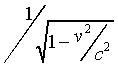 . This necessarily implies that even
a slow-moving object has a tiny mass increase if it is put in
motion.
. This necessarily implies that even
a slow-moving object has a tiny mass increase if it is put in
motion.
How does this mass increase relate to the kinetic energy? Consider
a mass m, moving at speed v, much less than the
speed of light. Its kinetic energy E =½mv²,
as discussed above. Its mass is 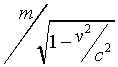 , which
we can write as m +dm, so dm is the tiny
mass increase we know must occur. It's easy to calculate dm.
For small v, we can make the approximations
, which
we can write as m +dm, so dm is the tiny
mass increase we know must occur. It's easy to calculate dm.
For small v, we can make the approximations
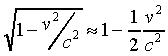
and
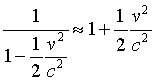
This means the total mass at speed v is m(1 + ½v²/c²), and writing this as m +dm, we see the mass increase dm equals ½ mv²/c². This means that again, the mass increase dm is related to the kinetic energy E by E = (dm)c2.
We have shown in the two sections above that when a force does
work to increase the kinetic energy of a particle it also causes
the mass of the particle to increase by an amount equal to the
increase in energy divided by c2. In fact this
result is exactly true over the whole range of speed from zero
to arbitrarily close to the speed of light, as we shall now demonstrate.
For a particle of mass m accelerating along a straight
line under a constant force F,
so
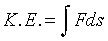
Now
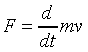 ,
,so
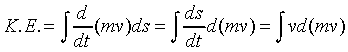
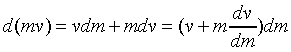
We find dv/dm:
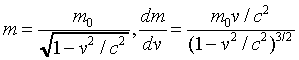
That is,
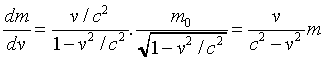
so
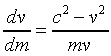
and
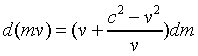
Therefore
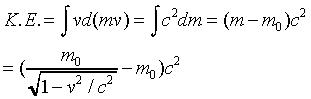
So we see that in the general case the work done on the body,
by definition its kinetic energy, is just equal to its mass increase
multiplied by c2.
To understand why this isn't noticed in everyday life, try an
example, such as a jet airplane weighing 100 tons moving at 2,000mph.
100 tons is 100,000 kilograms, 2,000mph is about 1,000 meters
per second. That's a kinetic energy ½Mv² of ½.1011joules,
but the corresponding mass change of the airplane down by the
factor c², 9.1016, giving an actual mass
increase of about half a milligram, not too easy to detect!
We use m0 to denote the "rest mass" of an object, and m to denote its relativistic mass,
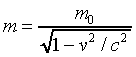 .
.
In this notation, we follow French and Feynman. Krane and Tipler,
in contrast, use m for the rest mass. Using m as we
do gives neater formulas for momentum and energy, but is not without
its dangers. One must remember that m is not a constant,
but a function of speed. Also, one must remember that the
relativistic kinetic energy is (m-m0)c2,
and not equal to ½mv2, even with
the relativistic mass!
Example: take v2/c2
= 0.99, find the kinetic energy, and compare it with ½mv2
(using the relativistic mass).
Physics 252 Home Page
Link to Next Lecture.
Copyright ©1997 Michael Fowler