
Michael Fowler
UVa Physics
Physics 252 Home Page
Link to Previous Lecture
Suppose we want to synchronize two clocks that are some distance
apart.
We could stand beside one of them and look at the other through
a telescope, but we'd have to remember in that case that we are
seeing the clock as it was when the light left it, and
correct accordingly.
Another way to be sure the clocks are synchronized, assuming they
are both accurate, is to start them together. How can we do that?
We could, for example, attach a photocell to each clock, so when
a flash of light reaches the clock, it begins running.

If, then, we place a flashbulb at the midpoint of the line joining the two clocks, and flash it, the light flash will take the same time to reach the two clocks, so they will start at the same time, and therefore be synchronized.
Let us now put this whole arrangement - the two clocks and the
midpoint flashbulb - on a train, and we suppose the train is moving
at some speed v to the right, say half the speed of light
or so.
Let's look carefully at the clock-synchronizing operation as seen
from the ground. In fact, an observer on the ground would say
the clocks are not synchronized by this operation! The
basic reason is that he would see the flash of light from the
middle of the train traveling at c relative to the ground
in each direction, but he would also observe the back of the train
coming at v to meet the flash, whereas the front is moving
at v away from the bulb, so the light flash must go further
to catch up.
In fact, it is not difficult to figure out how much later the
flash reaches the front of the train compared with the back of
the train, as viewed from the ground. First recall that as viewed
from the ground the train has length 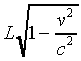 .
.
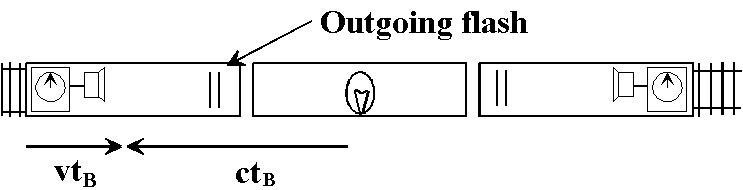
Letting tB be the time it takes the flash to reach the back of the train, it is clear from the figure that

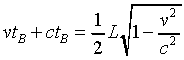
from which tB is given by
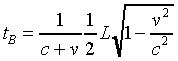 .
.In a similar way, the time for the flash of light to reach the front of the train is (as measured by a ground observer)
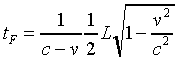
Therefore the time difference between the starting of the two
clocks, as seen from the ground, is
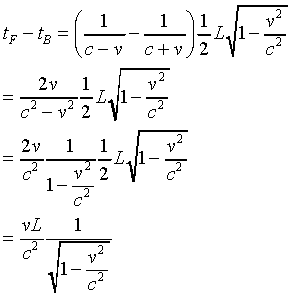
Remember, this is the time difference between the starting of
the train's back clock and its front clock as measured by an observer
on the ground with clocks on the ground. However, to this observer
the clocks on the train appear to tick more slowly, by the factor
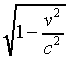 , so that although the ground observer
measures the time interval between the starting of the clock at
the back of the train and the clock at the front as
, so that although the ground observer
measures the time interval between the starting of the clock at
the back of the train and the clock at the front as 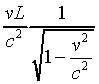 seconds, he also sees the slow running clock at the back actually
reading
seconds, he also sees the slow running clock at the back actually
reading 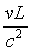 seconds at the instant he sees
the front clock to start.
seconds at the instant he sees
the front clock to start.
To summarize: as seen from the ground, the two clocks
on the train (which is moving at v in the x-direction)
are running slowly, registering only 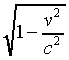 seconds for each second that passes. Equally important, the clocks-which
are synchronized by an observer on the train-appear unsynchronized
when viewed from the ground, the one at the back of the train
reading
seconds for each second that passes. Equally important, the clocks-which
are synchronized by an observer on the train-appear unsynchronized
when viewed from the ground, the one at the back of the train
reading 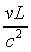 seconds ahead of the clock at
the front of the train, where L is the rest length of the
train (the length as measured by an observer on the train).
seconds ahead of the clock at
the front of the train, where L is the rest length of the
train (the length as measured by an observer on the train).
Note that if L = 0, that is, if the clocks are together,
both the observers on the train and those on the ground will agree
that they are synchronized. We need a distance between
the clocks, as well as relative motion, to get a disagreement
about synchronization.
Copyright ©1996 Michael Fowler