Michael Fowler
UVa Physics
The object of this exercise is to show explicitly how it is possible for two observers in inertial frames moving relative to each other at a relativistic speed to each see the other's clocks as running slow and as being unsynchronized, and yet if they both look at the same clock at the same time from the same place (which may be far from the clock), they will agree on what time it shows!
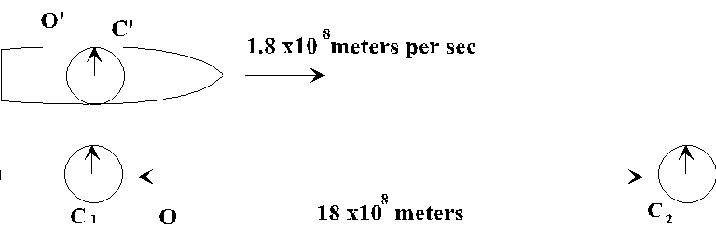
Suppose that in frame S we have two synchronized clocks C1 and C2 set 18 x 108 meters apart (that's about a million miles, or 6 light-seconds). A spaceship carrying a clock C' is traveling at 0.6c, that is 1.8 x 108 meters per second, parallel to the line C1C2, passing close by each clock.
Suppose C' is synchronized with C1 as
they pass, so both read zero.
As measured by an observer O in S - the "ground
frame" -- the spaceship will take just 10 seconds
to reach C2, since the distance is 6 light seconds,
and the ship is traveling at 0.6c.
What does clock C' (the clock on the ship) read as it passes
C2?
The time dilation factor 
,
so C', the ship's clock, will read 8 seconds.
Thus if both O, O' are at C2 as
C' passes C2 , both will agree that the
clocks look like:
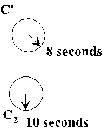
How, then, can O' claim that the clocks C1, C2
are the ones that are running slow?
To O', C1, C2 are
running slow, but remember they are not synchronized. To
O', C1 is behind C2
by 
seconds.
(From O' 's point of view, the two clocks can be imagined to be at the
front and back of an extremely long train rushing by her, so the one at
the "back" of the train -- the second one to pass her --
is the one that reads ahead in time, as we discussed
at length in the lecture on synchronizing clocks.)
Therefore, O' will conclude that since C2 reads 10 seconds as she passes it, at that instant C1 must be registering 6.4 seconds. O' 's own clock reads 8 seconds at that instant, so she concludes that C1 is running slow by the appropriate time dilation factor of 4/5. This is how the change in synchronization makes it possible for both O and O' to see the other's clocks as running slow.
Of course, O's assertion that as she passes the second
"ground" clock C2 the first "ground"
clock C1 must be registering 6.4 seconds is
not completely trivial to check! After all, that clock is now
a million miles away!
Let us imagine, though, that both observers are equipped with Hubble-style telescopes attached to fast acting cameras, so reading a clock a million miles away is no trick.
To settle the argument, the two of them agree that as she passes the second clock, the ground observer will be stationed at the second clock, and at the instant of her passing they will both take telephoto digital snapshots of the faraway clock C1, to see what time it reads.
The "ground" observer O, of course, knows that C1 is 6 light
seconds away, and is synchronized with C2 which
at that instant is reading 10 seconds, so his snapshot must show
C1 to read 4 seconds. That is, looking at C1
he sees it as it was six seconds ago.
What does O' 's digital snapshot show? It must be identical -- two snapshots taken from the same place at the same time must show the same thing! So, O' must also gets a picture of C1 reading 4 seconds.
How can she reconcile a picture of the clock reading 4 seconds
with her assertion that at the instant she took the photograph
the clock was registering 6.4 seconds?
The answer is that she can if she knows her relativity!
First point: length contraction. To O', the clock C1 is actually only 4/5 x 18 x 108 meters away (she sees the distance C1C2 to be Lorentz contracted!).
Second point: The light didn't even have to go that far! In her frame, the clock C1 is moving away, so the light arriving when she's at C2 must have left C1 when it was closer -- at distance x in the figure below. The figure shows the light in her frame moving from the clock towards her at speed c, while at the same time the clock itself is moving to the left at 0.6c. So the image of the first ground clock she sees as she passes the second ground clock must have been emitted when the first clock was a distance x from her in her frame, where x(1 + 3/5) = 4/5 x 18 x 108 m., so x = 9 x 108 meters.
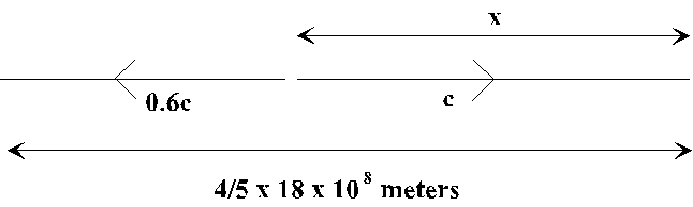
Third point: time dilation. The story so far: she has a photograph of the first ground clock that shows it to be reading 4 seconds. She knows that the light took three seconds to reach her. So, what can she conclude the clock must actually be registering at the instant the photo was taken? If you are tempted to say 7 seconds, you have forgotten that in her frame, the clock is moving at 0.6c and hence runs slow by a factor 4/5.
Including the time dilation factor correctly, she concludes that in the 3 seconds that the light from the clock took to reach her, the clock itself will have ticked away 3 x 4/5 seconds, or 2.4 seconds.
Therefore, since the photograph shows the clock to read 4 seconds, and she finds the clock must have run a further 2.4 seconds, she deduces that at the instant she took the photograph the clock must actually have been registering 6.4 seconds, which is what she had claimed all along!
Copyright © Michael Fowler, 1996