Michael Fowler
University of Virginia
Physics 252 Home Page
Link to Previous Lecture
As we have said, the wave nature of particles implies that
we cannot know both position and momentum of a particle
to an arbitrary degree of accuracy -- if delta_x
represents the fuzziness in our knowledge of position, and delta_p
that of momentum, then
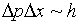
where h is Planck's constant. We formulated this by constructing
a wave packet moving along a line. In the real world, particles
are three dimensional and we should say
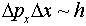
with corresponding equations for the other two spatial directions.
The fuzziness about position is related to that of momentum in
the same direction.
Let's see how this works by trying to measure y position
and y momentum very accurately. Suppose we have a source
of electrons, say, an electron gun in a CRT (cathode ray tube,
such as a monitor). The beam spreads out a bit, but if we interpose
a sheet of metal with a slit of width w, then for particles
that make it through the slit, we know y with an uncertainty
delta_y = w. Now, if the slit is a long way
downstream from the electron gun source, we also know py
very accurately as the electron reaches the slit, because to make
it to the slit the electron's velocity would have to be aimed
just right.
But does the measurement of the electron's y position --
in other words, having it go through the slit -- affect its y
momentum? The answer is yes. If it didn't, then sending a
stream of particles through the slit they would all hit very close
to the same point on a screen placed further downstream. But we
know from experiment that this is not what happens -- a single
slit diffraction pattern builds up, of angular width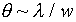 
,
where the electron's de Broglie wavelength lambda is given
by 
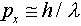(there is a negligible contribution
to lambda from the y-momentum). The consequent uncertainty
in py is
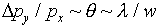
Putting in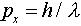 
, we find immediately that
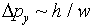
so the act of measuring the electron's y position has fuzzed out its y momentum by precisely the amount required by the uncertainty principle.
In order to understand the uncertainty principle better, let's
try to see what goes wrong when we actually try to measure position
and momentum more accurately than allowed.
For example, suppose we look at an electron through a microscope.
What could we expect to see? Of course, you know that if we try
to look at something really small through a microscope
it gets blurry-a small sharp object gets diffraction patterns
around its edges, indicating that we are looking at something
of size comparable to the wavelength of the light being used.
If we look at something much smaller than the wavelength of light-like
the electron-we would expect a diffraction pattern of concentric
rings with a circular blob in the middle. The size of the pattern
is of order the wavelength of the light, in fact from optics it
can be shown to be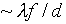
where d is the
diameter of the object lens of the microscope, f the focal
distance (the distance from the lens to the object). We shall
take f /d of order 1, as it usually is. So looking
at an object the size of an electron should give a diffraction
pattern centered on the location of the object. That would seem
to pin down its position fairly precisely.
What about the momentum of the electron? Here a problem
arises that doesn't matter for larger objects -- the light we
see has, of course, bounced off the electron, and so the electron
has some recoil momentum. That is, by bouncing light off the electron
we have given it some momentum. Can we say how much? To make it
simple, suppose we have good eyes and only need to bounce one
photon off the electron to see it. We know the initial momentum
of the photon (because we know the direction of the light beam
we're using to illuminate the electron) and we know that after
bouncing off, the photon hits the object lens and goes through
the microscope, but we don't know where the photon hit
the object lens. The whole point of a microscope is that all the
light from a point, light that hits the object lens in different
places, is all focused back to one spot, forming the image
(apart from the blurriness mentioned above). So if the light has
wavelength lambda, its constituent photons have momentum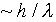
,
and from our ignorance of where the photon entered the microscope
we are uncertain of its x-direction momentum by an amount
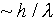. Necessarily, then, we have the same
uncertainty about the electron's x-direction momentum,
since this was imparted by the photon bouncing off.
But now we have a problem. In our attempts to minimize the uncertainty
in the electron's momentum, by only using one photon to detect
it, we are not going to see much of the diffraction pattern discussed
above-such diffraction patterns are generated by many photons
hitting the film, retina or whatever detecting equipment is being
used. A single photon generates a single point (at best!). This
point will most likely be within of order lambda of the
center of the pattern, but this leaves us with an uncertainty
in position of order lambda.
Therefore, in attempting to observe the position and momentum
of a single electron using a single photon, we find an uncertainty
in position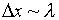 
, and in momentum 
.
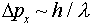These results are in accordance with Heisenberg's Uncertainty
Principle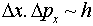 
.
Of course, we could pin down the position much better if we used
N photons instead of a single one. From statistical theory,
it is known that the remaining uncertainty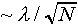
.
But then N photons have bounced off the electron, so, since
each is equally likely to have gone through any part of the object
lens, the uncertainly in momentum of the electron as a consequence
of these collisions goes up as sqrt N. (The same as the
average imbalance between heads and tails in a sequence of N
coin flips.)
Noting that the uncertainty in the momentum of the electron arises
because we don't know where the bounced-off photon passes through
the object lens, it is tempting to think we could just use a smaller
object lens, that would reduce delta_px.
Although this is correct, recall from above that we stated the
size of the diffraction pattern was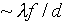 
,
where d is the diameter of the object lens and f
its focal length. It is easy to see that the diffraction pattern,
and consequently delta_x, gets bigger by just the
amount that delta_px gets smaller!
Suppose now that in the double slit experiment, we set out to
detect which slit each electron goes through by shining a light
just behind the screen and watching for reflected light from the
electron immediately after it had passed through a slit. Following
the discussion in Feynman's Lectures in Physics, Volume III,
we shall now establish that if we can detect the electrons, we
ruin the diffraction pattern!
Taking the distance between the two slits to be d, the dark lines in the diffraction pattern are at angles
.
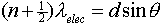If the light used to see which slit the electron goes through
generates an uncertainty in the electron's y momentum delta_py,
in order not to destroy the diffraction pattern we must have
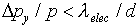
(the angular uncertainty in the electron's direction must not
be enough to spread it from the diffraction pattern maxima into
the minima). Here p is the electron's full momentum, 
.
Now, the uncertainty in the electron's y momentum, looking
for it with a microscope, is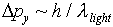 
.
Substituting these values in the inequality above we find the condition for the diffraction pattern to survive is
,
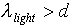the wavelength of the light used to detect which slit the electron
went through must be greater than the distance between the slits.
Unfortunately, the light scattered from the electron then gives
one point in a diffraction pattern of size the wavelength of the
light used, so even if we see the flash this does not pin down
the electron sufficiently to say which slit it went through.
Heisenberg wins again.
It is interesting to see how the actual physical size of the hydrogen atom is determined by the wave nature of the electron, in effect, by the Uncertainty Principle. In the ground state of the hydrogen atom, the electron minimizes its total energy. For a classical atom, the energy would be minus infinity, assuming the nucleus is a point (and very large in any case) because the electron would sit right on top of the nucleus. However, this cannot happen in quantum mechanics. Such a very localized electron would have a very large uncertainty in momentum-in other words, the kinetic energy would be large. This is most clearly seen by imagining that the electron is going in a circular orbit of radius r with angular momentum h/2.pi. Then one wavelength of the electron's de Broglie wave just fits around the circle, lambda = 2.pi.r. Clearly, as we shrink the circle's radius r, lambda goes down proportionately, and the electrons momentum p = h/lambda increases. Adding the electron's electrostatic potential energy we find the total energy for a circular orbit of radius r is:
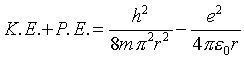
Notice that for small enough r, the kinetic energy term dominates, and the total energy grows as the atom shrinks. Evidently, there is a value of r for which the total energy is a minimum. This is easy to find by differentiating the total energy with respect to r and finding where it is zero. This gives
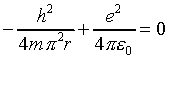
from which we find
.
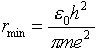The total energy for this radius is the exact right answer, which
is reassuring (but we don't deserve it, because we have used a
naïve picture, as will become clear later.)
The point of this exercise is to see that in quantum mechanics,
unlike classical mechanics, a particle cannot position itself
at the exact minimum of potential energy, because that would require
a very narrow wave packet and thus be expensive in kinetic energy.
The ground state of a quantum particle in an attractive potential
is a trade off between potential energy minimization and kinetic
energy minimization. Thus the physical sizes of atoms, molecules
and ultimately ourselves are determined by Planck's constant.
Physics 252 Home Page
Link to Next Lecture
Copyright ©1997 Michael Fowler