Some Further Notes on Blackbody Radiation

Michael Fowler

Thermodynamic Derivation of Stefan’s Law

In 1884, Poynting found expressions for the energy density, energy flow and momentum density and flow in an electromagnetic field: the energy density is $u = \frac{1}{2} (ε_{0} {\vec{E}}^{2} + {\vec{B}}^{2} / μ_{0})$ the energy flow rate is given by the Poynting vector, $\vec{S} = (\vec{E} \times \vec{B}) / μ_{0}$ , and the momentum density $\vec{P} = ε_{0} (\vec{E} \times \vec{B})$ . (We write these in MKS, he used cgs.)

For a plane wave, $B = E / c,$ ( $c = 1 / \sqrt{ε_{0} μ_{0}}$ ) so the energy density $u = ε_{0} {\vec{E}}^{2}$ and the momentum density $|\vec{P}| = ε_{0} {\vec{E}}^{2} / c$ . This was all deduced in the 1880’s from a fairly lengthy (but straightforward, see for example Jackson’s book) analysis of energy and momentum interchange between the electromagnetic field and charged particles. It’s easier to understand, though, using Einstein’s (later) discovery of $E = m c^{2} :$ the energy density $u$ corresponds to a mass density $ρ = u / c^{2},$ the momentum density for a plane wave is then $|\vec{P}| = ρ c = u / c .$ If we think of a light wave as having a finite total length, it follows that the energy-momentum relation must be

$E = c p .$

(Of course, this follows immediately from special relativity for massless particles, the point here is that it was previously known $—$ in the 1880’s $—$ from electromagnetic theory.)

Now imagine an oven filled with radiation, energy density $u,$ and consider the pressure on a wall. The argument is the same as for a gas of particles, except that the radiation travels at c and has energy-momentum relation $E = c p .$ Taking the radiation to be perfectly reflected, and all directions to be equally likely, one finds

$P = \frac{1}{3} u .$

(Imagine first the radiation to be all perpendicular to a wall: in the steady state, there would be momentum density $u / 2 c$ in each direction (towards the wall and away from it). A quantity $u c / 2 c$ would bounce off the wall each second, for a total momentum change (hence pressure!) of $u .$ In fact, only the perpendicular component of the radiation (which is going equally in all directions) counts, this gives the 1/3, exactly as for particles in the kinetic theory of gases.)

Another point: can we say the oven walls are perfectly reflecting? Didn’t we say they were black? Pippard points out that two such different ovens must, at the same temperature, have the same radiation distribution inside, or one could put a small pipe from one to the other and build a temperature difference, contradicting the Second Law.

At this point, we’re ready to apply standard thermodynamics to the radiation. Assume the oven filled with radiation is equivalent to a classical gas in a piston (so the volume can be adjusted).

Following Pippard (Classical Thermodynamics), the fundamental equation

$d U = T d S - P d V$

can be written in terms of energy and entropy densities $u = U / V, s = S / V,$ and remembering $P = \frac{1}{3} u,$ as

$d u = T d s + \frac{1}{V} (T s - \frac{4}{3} u) d V .$

But $u$ and $s$ only depend on temperature, not volume, so

$d u = T d s$

and therefore

$T s = \frac{4}{3} u .$

Hence

$\frac{d u}{d s} = T = \frac{\frac{4}{3} u}{s}$

$u = constant \times s^{4 / 3}$

from which

$u = a T^{4},$

completing the thermodynamic derivation of Stefan’s law.

Thermodynamic Derivation of Wien’s Displacement Law

The idea here is to expand a cubical container isotropically and slowly (so thermal equilibrium is maintained), allowing no heat transfer (adiabatic expansion). Imagining the radiation inside as standing waves in a reflecting box, the wavelengths will scale upwards with the dimensions of the box, so if we track waves of a particular wavelength, the wavelength will change as

$λ^{3} \propto V .$

(this argument is from Wannier’s book).

Now (from the previous section)

$P V = \frac{1}{3} U$

and in the adiabatic expansion $d S = 0,$ so

$d U = - P d V$

from which it is easy to check that the equation of the adiabat is

$P^{3 / 4} V = constant$

and since the radiation pressure goes as $T^{4},$

$T^{3} V = constant .$

Suppose now we track waves having frequency in the small interval $(f_{1}, f_{1} + d f_{1})$ as the volume increases slowly from $V_{1}$ to $V_{2} .$ The temperature will go from $T_{1}$ to $T_{2},$ the frequency range from $(f_{1}, f_{1} + d f_{1})$ to $(f_{2}, f_{2} + d f_{2}),$ and, from $λ f = c,$

$f_{1} = \frac{T_{1}}{T_{2}} f_{2}, d f_{1} = \frac{T_{1}}{T_{2}} d f_{2} .$

Now we know from the Stefan-Boltzmann law that the total radiation intensity changes as:

$\int_{0}^{\infty} ρ (f_{1}, T_{1}) d f_{1} = \frac{T_{1}^{4}}{T_{2}^{4}} \int_{0}^{\infty} ρ (f_{2}, T_{2}) d f_{2}$

Wien argued that Boltzmann’s thermodynamic analysis (previous section) could be applied to just the radiation in a small frequency interval, so one can conclude that

$ρ (f_{1}, T_{1}) d f_{1} = \frac{T_{1}^{4}}{T_{2}^{4}} ρ (f_{2}, T_{2}) d f_{2} .$

Changing notation: $T_{1}$ goes to $T, T_{2}$ goes to 1, $f_{1}$ goes to $f,$ we have

$ρ (f, T) = T^{3} ρ (\frac{f}{T}, 1)$

so apart from the overall factor $T^{3},$ the curve has exactly the same shape as a function of $f / T$ at all temperatures. This is exactly what is observed experimentally. In particular, if the radiation is most intense at frequency $f_{max},$ then we find Wien’s Displacement Law:

$f_{max} \propto T .$

The curve can equivalently be written

$ρ (f, T) = f^{3} g (\frac{f}{T}, 1),$

probably this form inspired Wien’s Radiation Law conjecture, $ρ (f) = α f^{3} e^{- β f / T}$ .

The Factor $¼$ for Radiation from a Hole

If one imagines an energy density $ρ (f, T)$ streaming down a pipe of cross-section area $A$ (the size of the hole) at speed $c,$ one would find radiation intensity $A c ρ (f, T) .$ So why the factor of $¼$ ? The energy density inside the oven has waves equally moving in opposite directions, so only half of it is moving the right way to get through the hole. Furthermore, it’s not all coming directly at the hole, it’s hitting it from all inside directions, and that coming in at an angle $θ$ to the vertical sees effectively a smaller hole, by a factor $\cos θ .$ Taking account of this, and adding radiation from all angles, gives the $¼$ .

How Planck Related the Energy Density in the Radiation Field to That in a Single Oscillator

He chose the simplest model possible: one linear oscillator (in the wall of the oven) driven at frequency $f = 2 π ω$ by a monochromatic oscillating electric field, the oscillator constantly damped by emitting energy as radiation.

It was well known from classical electrodynamics that an accelerating charge lost energy in this way, and it could be included in the oscillator dynamics as an effective damping force $- (2 e^{2} / 3 c^{3}) \overset{⃛}{x},$ so the equation of motion is

$m \ddot{x} + m ω_{0}^{2} x - (2 e^{2} / 3 c^{3}) \overset{⃛}{x} = e E \cos ω t$

$m ω_{0}^{2}$ being the usual spring constant. (Note: these are Planck’s cgs units. In MKS, we should replace $e^{2}$ by $e^{2} / 4 π ε_{0},$ but we won’t bother to add that clutter, since the $e^{2}$ terms cancel out in the final result.)

This can be further simplified by the following trick: the oscillator is driven at the external frequency $f = 2 π ω,$ one can (at least for small damping) write

$- (2 e^{2} / 3 c^{3}) \overset{⃛}{x} = - (2 e^{2} / 3 c^{3}) ω^{2} \dot{x} = - γ \dot{x}$ ,

say. This is now a familiar equation, an oscillator in a viscous medium with a drag force proportional to velocity, and is readily solved, most simply by using complex numbers. The amplitude $A$ of the driven oscillations is:

$A = \frac{e E}{\sqrt{m^{2} {(ω_{0}^{2} - ω^{2})}^{2} + {(γ ω)}^{2}}} .$

The oscillator has energy $U = \frac{1}{2} m ω_{0}^{2} A^{2} .$ For small damping, there is a sharp maximum at the natural frequency of the oscillator, $ω_{0} .$

To summarize: the physics of the above model is that the charged oscillator is being driven by the single-frequency external electromagnetic field, which is therefore feeding energy into the oscillator, which energy is constantly being drained out by radiation damping, that is, emission of outgoing radiation at the same frequency $—$ so in the steady state the oscillator is in equilibrium with the external field.

Planck’s next step was to place this oscillator in a real radiation field, so the single frequency driving source is replaced by a very large number of driving fields at all different frequencies, and with no overall coherence. (If we take the oven to have reflective walls, there will be one driving field for each allowed standing wave, counting also a factor of two for polarization.) But there’s a big simplification: if we take the damping to be small, the only significant driving frequencies are those close to the natural frequency of the oscillator, where

$\begin{matrix} U = \frac{1}{2} m ω_{0}^{2} A^{2} \\ = \frac{1}{2} m ω_{0}^{2} \frac{e^{2} E^{2}}{m^{2} {(ω_{0}^{2} - ω^{2})}^{2} + {(γ ω)}^{2}} \\ ≅ \frac{1}{2} m ω_{0}^{2} \frac{e^{2}}{4 m^{2} ω_{0}^{2} {(ω_{0} - ω)}^{2} + {(γ ω_{0})}^{2}} E^{2} \\ = \frac{1}{8 m} \frac{e^{2}}{{(ω_{0} - ω)}^{2} + {(γ / 2 m)}^{2}} E^{2} . \end{matrix}$

Now, going from a single driving field to an actual radiation field amounts to summing over the modes inside the narrow peak at $ω_{0} .$ The weight can be found by integration: it’s

$\frac{π e^{2}}{8 m} \frac{2 m}{γ} = \frac{π e^{2}}{4} \frac{3 c^{3}}{2 e^{2} ω_{0}^{2}} = \frac{3 π c^{3}}{8 ω_{0}^{2}},$

from which:

$E^{2} = \frac{8 ω_{0}^{2}}{3 π c^{3}} U .$

Now this is only the $x$ -component of the radiation field, going to the full field gets rid of the 3 in the denominator. The energy density in (radial) frequency in the radiation field is then found by replacing

$E^{2} / 2 \to 4 π ρ (ω, T),$

giving

$ρ (ω_{0}, T) = \frac{ω_{0}^{2}}{3 π^{2} c^{3}} U,$

or in terms of frequency in cycles per second,

$ρ (f, T) = (8 π f^{2} / c^{3}) U (f, T)$

where $U (f, T)$ is the energy of the oscillator, $ρ (f, T)$ the radiation energy intensity.

Radiation Damping and Reversibility

It is perhaps worth noting that although the radiation term is formally equivalent to a viscous damping term, it does not produce “heat” in quite the same way $—$ the energy lost goes back into the driving system, and the damping constant is not arbitrary, but related to the driving coupling. Planck believed at first that this absorption of radiation and reemission was irreversible, in line with the Second Law. But Boltzmann pointed out to him that the electromagnetic processes were reversible, just as mechanical processes were, so this couldn’t be quite right.

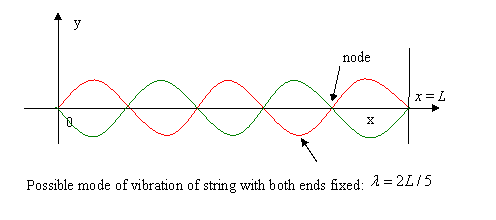
Counting the Electromagnetic Standing Wave Modes in the Oven

To make any quantitative progress in analyzing the radiation, we must have a clear picture of the degrees of freedom of this system: how many oscillators have frequencies in a given energy range? These oscillations are standing electromagnetic waves. The waves are contained in the oven, so the electric field intensity drops rapidly to zero on approaching and going into the walls, because inside the walls the electric energy will be rapidly dissipated by currents or polarization. In fact, then, the boundary condition at the walls is much like that for waves on a string fixed at both ends, where the wave amplitude goes to zero at the ends.

As a warm up exercise, consider the frequency distribution function of the possible different modes of vibration (that is, the different degrees of freedom) of a string stretched between two points a distance L apart.

Possible values of the wavelength are:

$λ = 2 L, L, 2 L / 3, \dots$

so the frequency

$f = c / λ = c / 2 L, 2 (c / 2 L), 3 (c / 2 L), \dots$

The allowed frequencies are thus equally spaced $c / 2 L$ apart. We define the spectral density by stating that the number of modes between $f$ and $f + Δ f$ is $N (f) Δ f$ for $Δ$ small compared with the range of frequencies in the system, but large compared with the spacing between successive allowed frequencies. Evidently, in this simple one-dimensional example $N (f)$ is a constant equal to $2 L / c .$

The amplitude of oscillation as a function of time has the form:

$y = A \sin \frac{2 π x}{λ} \sin 2 π f t .$

This is more conveniently written:

$y = A \sin k x \sin ω t$

where

$k = 2 π / λ, ω = 2 π f = c k$

using $λ f = c .$

Here $ω$ is of course the radial frequency $—$ how many radians per second, rather than cycles per second, the time dependent component of the wave moves through. Analogously, $k,$ called the wave number, counts the radians of spatial change in unit length (one meter in SI, but note that practicing physicists often still use CGS).

We are now ready to tackle the more complex problem of three-dimensional standing electromagnetic waves in a cubical oven. The first guess, just generalizing the expression above, would be:

$\vec{E} (\vec{r}, t) = {\vec{E}}_{0} \sin k_{x} x \sin k_{y} y \sin k_{z} z \sin ω t .$

This will satisfy the wave equation

${\vec{\nabla}}^{2} \vec{E} - \frac{1}{c^{2}} \frac{\partial^{2} \vec{E}}{\partial t^{2}} = 0$

$ω^{2} = c^{2} (k_{x}^{2} + k_{y}^{2} + k_{z}^{2}) .$

Also the electric field will be zero at all the walls if we choose the $k$ ’s appropriately, that is, so that $\sin k_{x} L = 0,$ etc.

However, this wave is not quite correct!

There is no electric charge in the oven away from the walls, so the divergence of the electric field, $\vec{\nabla} \cdot \vec{E} = ρ / ε_{0},$ must be identically zero away from the walls, a condition this wave does not satisfy. The divergence is:

$\begin{matrix} \vec{\nabla} \cdot \vec{E} (\vec{r}, t) = E_{0 x} k_{x} \cos k_{x} x \sin k_{y} y \sin k_{z} z \sin ω t \\ + E_{0 y} k_{y} \sin k_{x} x \cos k_{y} y \sin k_{z} z \sin ω t \\ + E_{0 z} k_{z} \sin k_{x} x \sin k_{y} y \cos k_{z} z \sin ω t \end{matrix}$

and, for example, taking any $x$ for which $\sin k_{x} x = 0,$ the second and third terms above are identically zero, but the first term certainly isn’t.

This problem can be fixed by thinking more carefully about the boundary conditions at the walls. It is true that any component of the electric field parallel to the wall will be attenuated rapidly by currents or polarization in the wall. However, there could be an electric field perpendicular to the wall, because there could be surface charge on the wall.

This means a possible solution is:

$\begin{matrix} E_{x} (\vec{r}, t) = E_{0 x} \cos k_{x} x \sin k_{y} y \sin k_{z} z \sin ω t \\ E_{y} (\vec{r}, t) = E_{0 y} \sin k_{x} x \cos k_{y} y \sin k_{z} z \sin ω t \\ E_{z} (\vec{r}, t) = E_{0 z} \sin k_{x} x \sin k_{y} y \cos k_{z} z \sin ω t . \end{matrix}$

These components are deliberately chosen to give

$\begin{matrix} \vec{\nabla} \cdot \vec{E} (\vec{r}, t) = (k_{x} E_{0 x} + k_{y} E_{0 y} + k_{z} E_{0 z}) \sin k_{x} x \sin k_{y} y \sin k_{z} z \sin ω t \\ so choosing \vec{k} such that \vec{k} \cdot {\vec{E}}_{0} = 0, we find \vec{\nabla} \cdot \vec{E} = 0. \end{matrix}$

This is telling us something we should have realized from the beginning: in the standing electromagnetic wave in the cavity, just as in a propagating wave, the electric field is perpendicular to the direction in which the wave is moving. In other words, it is a transverse wave, and in fact there are two independent polarizations, which we must remember to count when we find the total number of degrees of freedom.

It remains to find the allowed frequencies of vibration $—$ the normal modes $—$ of the electromagnetic radiation in the oven. The first step is to find the allowed values of the wave numbers $k_{x}, k_{y}, k_{z} .$ These are fixed by the boundary conditions $\sin k_{x} L = 0,$ etc., so

$k_{x, y, z} = π / L, 2 π / L, 3 π / L, \dots$

so the vector

$\vec{k} = (k_{x}, k_{y}, k_{z}) = \frac{π}{L} (l, m, n)$

Where $(l, m, n)$ are positive integers, like (1, 1, 1) or (5, 13, 4): in other words, each possible standing electromagnetic wave in the oven corresponds to a point in the $(k_{x}, k_{y}, k_{z})$ space labeled by three positive integers. These are the intersection points of a cubic lattice in the space $k_{x} > 0, k_{y} > 0, k_{z} > 0.$

Each such point can be associated with the little lattice cube of volume ${(π / L)}^{3}$ for which the point in question is the furthest corner of the little cube from the $k$ -space origin. These little cubes stack together to fill all that part of $k$ -space having $k_{x} > 0, k_{y} > 0, k_{z} > 0.$

The frequency of vibration of the wave having wave numbers $(k_{x}, k_{y}, k_{z})$ is

$ω = c \sqrt{k_{x}^{2} + k_{y}^{2} + k_{z}^{2}} .$

Recall that the experimental measurement of black body radiation from the oven detects the intensity of radiation in a given frequency range. It does not tell us the wave numbers of the radiating modes! Hence, to compare with these experimental results, we must choose a small frequency range and find how many possible sets of wave numbers correspond to modes of vibration having frequencies within that range.

Notice that a fixed value of the frequency corresponds to a spherical surface in $k$ -space:

$\frac{ω^{2}}{c^{2}} = k_{x}^{2} + k_{y}^{2} + k_{z}^{2} .$

Therefore, the number of possible modes of radiation in the oven having frequencies in the range $(ω, ω + Δ ω)$ is equal to the number of lattice-point wave number values $(k_{x}, k_{y}, k_{z})$ between two spherical surfaces centered at the origin and having radii $(ω / c, (ω + Δ ω) / c),$ and only counting in the positive octant, $k_{x} > 0, k_{y} > 0, k_{z} > 0.$ Now, as we argued above, each lattice point can be associated with a small cube of volume ${(π / L)}^{3} .$ Assuming we choose $Δ ω / c > > π / L,$ there will be many of these small cubes between the spherical surfaces, and the total number of lattice points between the spheres in the positive octant will be just the volume of the space between the spheres divided by the volume of one of these cubes.

So the number of possible modes of radiation in the oven having frequencies in the range $(ω, ω + Δ ω)$ is:

$\frac{(1 / 8) \times 4 π {(ω / c)}^{2} Δ (ω / c)}{{(π / L)}^{3}} = (L^{3} / 2 π^{2}) {(ω / c)}^{2} Δ (ω / c) .$

Putting this in terms of the frequency $f$ in cycles per second, $ω = 2 π f,$ and inserting an extra factor of two for the two independent polarizations of the wave (discussed above) we find the distribution function for modes in frequency is given by:

$N (f) d f = \frac{8 V π f^{2} d f}{c^{3}}$

where $V = L^{3}$ is the volume of the oven.