Planck’s Route to the Black Body Radiation Formula and Quantization

Michael Fowler

Wien’s Radiation Law

Wien proved using classical thermodynamics that the shape of the black body curve didn’t change with temperature, the curve just grew and expanded. However, the thermodynamic methods didn’t specify the actual shape. In 1893, Wien made a guess, based on the experimental data:

$ρ (f) = α f^{3} e^{- β f / T},$

his Radiation Law. $α, β$ are constants. In fact, this provided an excellent fit: it seemed that Kirchhoff’s challenge had at last been met! But the long wavelength low frequency measurements were not very precise, and when improved infrared technology was introduced a few years later, in 1900, it became clear that at the lowest frequencies $ρ (f)$ went as $f^{2},$ not $f^{3},$ and furthermore the radiation intensity at these low frequencies was proportional to the temperature. So Wien’s formula was wrong. The challenge was still there.

Planck’s Thermodynamic Approach: Oscillators in the Oven Wall

Photo Courtesy of the Clendening History of Medicine Library, University of Kansas Medical Center, Wikipedia Commons.

After what’s happened in physics over the last century or so, it’s difficult to appreciate the mindset of a physicist like Planck in the late 1890’s. He was forty years old and a well-established theorist at the University of Berlin. His earlier work had been in chemical physics, where applying thermodynamics had led to brilliant successes. He was convinced thermodynamics was the key to understanding nature at the deepest level. He spent years clarifying the subtleties of the Second Law (that entropy always increases). He believed the Second Law was rigorously correct, and would eventually be proved so in a more fundamental theory.

And now thermodynamics had made a good start in analyzing black body radiation, with proofs of Stefan’s Law and Wien’s Displacement Law. It seemed very likely that thermodynamics would yield the whole black body radiation curve. He felt this curve was the key to understanding just how electromagnetic radiation and matter exchanged energy. This was one of the basic problems in physics, and of obvious technological importance. And, in fact, just at that time experimentalists at his university were measuring the black body radiation curve to new levels of precision.

(Boltzmann himself had gone on to a molecular analysis of the properties of gases, relating thermodynamic quantities to microscopic distributions of particles. Planck was not impressed by this approach, since it implied that the Second Law was only statistical, only valid in the limit of large systems. However, he was fairly familiar with Boltzmann’s work $—$ he’d taught it in some of his classes, to present all points of view. Planck wasn’t sure, though, that atoms and molecules even existed.)

But how to begin a thermodynamic analysis of black body radiation? The oven used by the experimentalists was a dauntingly complex system: the hot oven walls contained many tiny oscillating electrical charges, the electromagnetic radiation from the acceleration of these charges being the heat and light radiation in the oven. At the same time, the wall oscillators were supplied with energy by the oscillating electrical fields of the radiation. In other words, at a steady temperature, the radiation inside the oven and the electrical oscillators in the walls were in thermal equilibrium, there was no net transfer of energy from one to the other over time, but small amounts of energy were constantly being traded back and forth for individual oscillators.

Fortunately, Kirchhoff had long ago proved that the details of the oven didn’t matter: if two ovens at the same temperature had different radiation intensity at some particular frequency, energy could flow from one to the other, violating the Second Law. So Planck could consider as his “oven” the simplest possible material object that would interact with the radiation: he took a simple harmonic oscillator (one-dimensional, mass $m,$ linear restoring force $- m ω_{0}^{2} x$ ). As a preliminary exercise, he replaced the incoherent heat radiation with a monochromatic oscillating electric field $E \cos ω t$ driving the oscillator. The model oscillator carried a charge $e .$ It was well-established in electromagnetic theory that an accelerating charge loses energy by emitting radiation, the effective drag force being $(2 e^{2} / 3 c^{3}) \overset{⃛}{x} .$

The oscillator equation of motion is therefore:

$m \ddot{x} + m ω_{0}^{2} x - (2 e^{2} / 3 c^{3}) \overset{⃛}{x} = e E \cos ω t .$

For the driven oscillator, Planck took $\overset{⃛}{x} = - ω^{2} \dot{x},$ giving a standard classical mechanics problem: the driven simple harmonic oscillator with viscous damping. This he solved to find the energy in the oscillator in terms of the strength of the driving field. (The details of his argument are given in the notes accompanying this lecture.)

A Classical Result Relating Radiation Intensity to Oscillator Energy

Planck next replaced the single driving field by the incoherent field of radiation in an oven in equilibrium at temperature $T .$ This is a completely different scenario! With the single driving field, after initial transient behavior, the oscillator settles down at a fixed amplitude and phase entrained to the driving force. But with many incoherent driving fields, even though the important ones turn out to be those close to the natural frequency of the oscillator, its motion will no longer much resemble a clock pendulum, more like an outdoor hanging basket in chaotic weather. However, Planck was considering energy exchange, he was not interested in a detailed description of the motion; the energy in the oscillator goes as the square of the driving field, and with many incoherent fields driving, the total oscillator energy is just the sum from each separately (cross terms will average to zero).

He was able to establish from his analysis (see the notes) an important correspondence between the wall oscillator’s mean energy $U (f, T)$ and the energy density $ρ (f, T)$ per unit frequency in the radiation field:

$ρ (f, T) = (8 π f^{2} / c^{3}) U (f, T) .$

It’s worth emphasizing that this is a classical result: the only inputs are classical dynamics, and Maxwell’s electromagnetic theory. Notice that the charge $e$ of the oscillator doesn’t appear: the result is independent of the coupling strength between the oscillator and the radiation, the coupling only has to be strong enough to ensure thermal equilibrium.

Oscillator Thermodynamics: Planck Focuses on Entropy

Armed with this new connection between the black body curve and the energy of an oscillator, Planck realized that from Wien’s Radiation Law,

$ρ (f) = α f^{3} e^{- β f / T},$

he could work out completely the thermodynamics of an oscillator. From his Second Law perspective, the natural approach was to see how the entropy varied with energy, the energy being given (from the two equations above) by

$U (f) = \frac{α c^{3} f}{8 π} e^{- β f / T} .$

He wrote down the corresponding expression for the entropy:

$S = - \frac{U}{β f} (\ln \frac{8 π U}{α f c^{3}} - 1) .$

Exercise: prove $T d S = d U .$

An important quantity in thermodynamics is the second derivative of the entropy, this is closely related to the Second Law: negativity of the second derivative guarantees that the entropy will increase back to equilibrium if the system is disturbed.

He found an elegant result:

$\frac{\partial^{2} S}{\partial U^{2}} = - \frac{1}{β f U},$

guaranteed to be negative! He was impressed by this simplicity, and thought he must be close to a deep thermodynamic truth. He went on to argue that this indicated the Second Law plus Wein’s displacement law most likely determined the black body curve uniquely. He was wrong.

Of course, it had been well known for years that statistical mechanics applied to an oscillator gives it energy $k T .$ Why Planck didn’t even mention this is a total mystery. He was familiar with Boltzmann’s work, but he really didn’t care for statistical mechanics. He was an old-fashioned thermodynamics guy.

New Experiments, New Theory

In October 1900, Rubens and Kurlbaum in Berlin announced some new experimental findings: the radiation intensity at low frequencies went as $f^{2},$ not $f^{3},$ and the low frequency intensity was proportional to the temperature.

This shook Planck. His simple result for an oscillator, $\partial^{2} S / \partial U^{2} = - 1 / β f U,$ was still very close to the truth for high frequencies, but at low frequencies equipartition was holding, the oscillator energy being $U = k T .$ Together with $d U = T d S,$ this gave immediately $\partial^{2} S / \partial U^{2} = - k / U^{2} .$

This certainly meant that his previous argument that the curve was uniquely determined by $\partial^{2} S / \partial U^{2} = - 1 / β f U$ had to be wrong. Abandoning thoughts of deep thermodynamic truths, he decided he’d better patch things up as best he could. How do you get from $\partial^{2} S / \partial U^{2} = - k / U^{2}$ at low frequencies to $\partial^{2} S / \partial U^{2} - 1 / β f U$ at high frequencies? Well, there’s one simple way:

$\partial^{2} S / \partial U^{2} = - \frac{k}{U (h f + U)} .$

(I’ve put in the correct values for the two parameters here: $k$ is Boltzmann’s constant, necessary to match the low frequency equation, the constant $β$ in Wien’s formula turns out to be Planck’s constant divided by Boltzmann’s constant, $β = h / k .$ )

This was of course a completely unjustified guess. But pressing on, integrating twice gives the entropy:

$S = k [(1 + U / h f) \ln (1 + U / h f) - (U / h f) \ln (U / h f)]$

from which

$\frac{d S}{d U} = \frac{k}{h f} [\ln (1 + \frac{U}{h f}) - \ln \frac{U}{h f}] = \frac{1}{T},$

giving

$U = \frac{h f}{e^{h f / k T} - 1} .$

This yields the radiation curve:

$ρ (f, T) = \frac{8 π f^{2}}{c^{3}} \frac{h f}{e^{h f / k T} - 1}$

(energy per unit volume) where $k$ is Boltzmann’s constant and $h$ is a new constant, now known as Planck’s constant.

This worked brilliantly! Of course, it matched Wien’s formula for high frequencies, and was proportional to $T$ at low frequencies. But it turned out to be far better: it matched the new high precision measurements within their tiny limits of error, throughout the entire range.

The Great Breakthrough: Birth of the Quantum

This surprisingly good news had Planck desperately searching for some theoretical justification! As always, he focused on his formula for the entropy (from his guessed second derivative, $\partial^{2} S / \partial U^{2},$ as discussed in the previous section):

$S = k [(1 + U / h f) \ln (1 + U / h f) - (U / h f) \ln (U / h f)] .$

How could this expression be interpreted? Here things took a very unexpected turn. Ironically, his familiarity with Boltzmann’s analysis of the entropy of a gas of atoms provided the clue, even though Planck himself doubted the existence of atoms!

Boltzmann’s expression for entropy $S$ is

$S = k \ln W$

where $W$ is the volume of microscopic phase space corresponding to given macroscopic variables, and $k$ is Boltzmann’s constant. (In fact this formulation, which appears on Boltzmann’s grave, was first written down by Planck.)

In 1877, Boltzmann actually analyzed a model system of atoms having entropy very close to the expression Planck had found. Boltzmann’s model allowed the atoms to have only energies which were integer multiples of a small fixed energy $ε .$ He then found the number of possible arrangements of atoms corresponding to a given total energy. This combinatorial analysis, using Stirling’s formula $\ln N! ≅ N \ln N - N,$ gave him expressions for the entropy. Finally, Boltzmann took the limit of small $ε .$

How would a similar analysis work for the harmonic oscillator? Again, one of Boltzmann’s ideas proved useful. The entropy of an oscillator having mean energy $U$ at temperature $T$ is related to the volume of phase space the oscillator is knocked around in by the thermal noise interactions. In 1884, Boltzmann had introduced the concept of an ensemble: for the oscillator, this would be a large collection of $N$ identical oscillators, with random phases but all the same $U$ and $T,$ so that at one instant in time the whole collection will represent the possible states of the single oscillator over time.

The ensemble then has entropy $N S,$ where $S$ is the entropy of the single oscillator. The entropy of the ensemble is $N S = N k \ln W .$ Now Planck’s guessed entropy

$S = k N [(1 + U / h f) \ln (1 + U / h f) - (U / h f) \ln (U / h f)],$

so using Boltzmann’s formula relating entropy to volume of phase space $W,$

$\ln W = N [(1 + U / h f) \ln (1 + U / h f) - (U / h f) \ln (U / h f)] .$

The possible different arrangements of the $N$ oscillators amount to: How many different ways can total energy $N U$ be shared among the $N$ oscillators? This is the total phase space that $W$ measures. In fact, Planck realized, probably remembering Boltzmann’s work, that his expression for $W$ (above) closely resembles a well-known combinatorial expression: how many ways can $M$ objects by distributed among $N$ boxes, if we assume the objects are all identical? The answer is

$W^{'} = \frac{(N + M - 1)!}{M! (N - 1)!} .$

(Proof: put $M$ dots on a line, with $N - 1$ vertical lines interspersed. These lines are the division from one box to the next. $W^{'}$ above is the total number of ways of doing this, since the dots are all identical, and so are the lines.)

For large values of $N, M,$ using Stirling’s formula $\ln N! ≅ N \ln N - N,$ this becomes

$\ln W^{'} = N [(1 + M / N) \ln (1 + M / N) - (M / N) \ln (M / N)] .$

And, staring first at this formula (or just remembering it?) and then at his expression for $W,$ it dawned on Planck that they are identical: $W = W^{'},$ provided

$\frac{U}{h f} = \frac{M}{N}, or N U = M h f .$

That is to say, the total energy $N U$ of Planck’s array of $N$ identical oscillators of frequency $f$ is $M h f,$ and $—$ crucially $—$ the entropy expression tells us this energy is distributed among the oscillators in discrete chunks each of size $h f .$

Planck did this work by December 1900, in two intense months after learning the new experimental results and feeling he had to justify his curve that fit so well. But he only half believed it. After all, the first part of his derivation, identifying the energy of an oscillator with that in the radiation field, was purely classical: he’d assumed the emission and absorption of energy to be continuous. Then, he suddenly changed the story, moving to a totally nonclassical concept, that the oscillators could only gain and lose energy in chunks, or quanta. (Incidentally, it didn’t occur to him that the radiation itself might be in quanta: he saw this quantization purely as a property of the wall oscillators.) As a result, although the exactness of his curve was widely admired, and it was the Birth of the Quantum Theory (with hindsight), no-one $—$ including Planck $—$ grasped this for several years!

Meanwhile in England...

Lord Rayleigh was working on the same problem. He’d heard about Wien’s Radiation Law $ρ (f) = α f^{3} e^{- β f / T}$ but he didn’t believe it $—$ for one thing, it predicted that if you detected radiation at one frequency as the oven heated up, beyond a certain temperature, according to Wien, the radiation intensity would barely increase, tending to the limit $α f^{3} .$ As Rayleigh pointed out in May, 1900, this seemed very implausible $—$ and, in the infrared, the effect should be detectable by those excellent Berlin experimentalists who had (apparently!) confirmed Wien’s Law. He was of course correct. At the same time, he proposed changing the law from Wien’s form to $ρ (f) = c_{1} f^{2} T e^{- c_{2} f / T},$ Rayleigh’s Radiation Law. This would ensure that for a particular frequency, the radiation intensity at high enough temperature would become linear in $T,$ a much more reasonable result, in accord with equipartition. He published a two-page paper making this point in June, 1900. But his Law didn’t last long: in October 1900, Rubens and Kurlbaum’s very precise infrared measurements showed his predicted curve was just outside their error bars (the plot is $ρ$ versus $T$ in the infrared, wavelength $λ =$ 51.2 microns. The solid line is observation, Rayleigh is dot-dash, note Wien is hopeless):

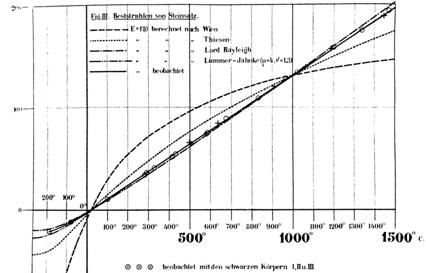
Rayleigh’s rationale for the $f^{2}$ low frequency behavior is detailed in the lecture on Black Body Radiation: he took the radiation to be a collection of standing waves in a cubical enclosure: electromagnetic oscillators, and found all the allowed such standing waves for each frequency interval. He proved that the density of such modes of vibration as a function of frequency went as $f^{2} .$ So assuming equipartition of energy, obviously nonsense at high frequencies, but as Rayleigh commented: “… although for some reason not yet explained the doctrine fails in general, it seems possible it may apply to the graver modes” meaning the low frequency modes. He was quite right.

Rubens and Kurlbaum show Rayleigh’s curve on their graph reproduced above. However, they give equal billing to some other curves, all of which are really guesses. They didn’t apparently realize that Rayleigh’s curve was based on theory. More remarkably, Planck refers explicitly to their paper in his December 1900 work $—$ yet does not mention Rayleigh’s work. Perhaps this is a question of style $—$ possibly Rayleigh’s paper, just two pages long, called “Remarks”, and with the appearance of having being written in an hour or two, didn’t impress the Berliners. This was a pity, because Rayleigh’s approach, based on standing electromagnetic waves, proved most fruitful when it was taken up, or perhaps rediscovered, by Einstein years later.

Sources

Planck wrote that in the 1890’s “I had been inclined to reject atomism”, quoted in Niels Bohr’s Times, Abraham Pais, page 104.

Wien’s Displacement Law: Ann. der Phys. 52, 132 (1894), M. J. Klein’s article in History of Twentieth Century Physics, Academic Press, 1977.

Boltzmann himself was very unsure how well oscillators came to equilibrium with electromagnetic radiation: his paper in Nature, 51, 413, 1895.

Lord Rayleigh was working on the same problem. He’d heard about Wien’s Radiation Law $ρ (f) = α f^{3} e^{- β f / T}$ and he didn’t believe it. Phil. Mag. 49, 539, 1900.

Rayleigh comments: “… although for some reason not yet explained the doctrine fails in general, it seems possible it may apply to the graver modes” $-$ same article.