The Michelson-Morley Experiment
Michael Fowler, University of Virginia
The Nature of Light
As a result of Michelson’s efforts in 1879, the speed of light was known to be 186,350 miles per second with a likely error of around 30 miles per second. This measurement, made by timing a flash of light travelling between mirrors in Annapolis, agreed well with less direct measurements based on astronomical observations. Still, this did not really clarify the nature of light. Two hundred years earlier, Newton had suggested that light consists of tiny particles generated in a hot object, which spray out at very high speed, bounce off other objects, and are detected by our eyes. Newton’s arch-enemy Robert Hooke, on the other hand, thought that light must be a kind of wave motion, like sound. To appreciate his point of view, let us briefly review the nature of sound.
The Wavelike Nature of Sound
Actually, sound was already quite well understood by the ancient Greeks. The essential point they had realized is that sound is generated by a vibrating material object, such as a bell, a string or a drumhead. Their explanation was that the vibrating drumhead, for example, alternately pushes and pulls on the air directly above it, sending out waves of compression and decompression (known as rarefaction), like the expanding circles of ripples from a disturbance on the surface of a pond. On reaching the ear, these waves push and pull on the eardrum with the same frequency (that is to say, the same number of pushes per second) as the original source was vibrating at, and nerves transmit from the ear to the brain both the intensity (loudness) and frequency (pitch) of the sound.
There are a couple of special properties of sound waves (actually any waves) worth mentioning at this point. The first is called interference. This is most simply demonstrated with water waves. If you put two fingers in a tub of water, just touching the surface a foot or so apart, and vibrate them at the same rate to get two expanding circles of ripples, you will notice that where the ripples overlap there are quite complicated patterns of waves formed. The essential point is that at those places where the wave-crests from the two sources arrive at the same time, the waves will work together and the water will be very disturbed, but at points where the crest from one source arrives at the same time as the wave trough from the other source, the waves will cancel each other out, and the water will hardly move.
There's a standard physics lab experiment illustrating this point, it's called two-slit interference. A monochromatic plane wave approaches a screen in which there are two narrow slit openings. If the slit opening width is smaller than the wavelength, a single slit will give approximately semicircular waves coming out the other side, the disturbance radiates out from the slit. The two slits together show the pattern generated by interference. It's best seen by clicking on this applet. Watch how the pattern changes with wavelength and with slit separation.
You can hear the interference effect for sound waves by playing a constant note through stereo speakers. As you move around a room, you will hear quite large variations in the intensity of sound. Of course, reflections from walls complicate the pattern. This large variation in volume is not very noticeable when the stereo is playing music, because music is made up of many frequencies, and they change all the time. The different frequencies, or notes, have their quiet spots in the room in different places. The other point that should be mentioned is that high frequency tweeter-like sound is much more directional than low frequency woofer-like sound. It really doesn’t matter where in the room you put a low-frequency woofer—the sound seems to be all around you anyway. On the other hand, it is quite difficult to get a speaker to spread the high notes in all directions. If you listen to a cheap speaker, the high notes are loudest if the speaker is pointing right at you. A lot of effort has gone into designing tweeters, which are small speakers especially designed to broadcast high notes over a wide angle of directions.
Is Light a Wave?
Bearing in mind the above minireview of the properties of waves, let us now reconsider the question of whether light consists of a stream of particles or is some kind of wave. The strongest argument for a particle picture is that light travels in straight lines. You can hear around a corner, at least to some extent, but you certainly can’t see. Furthermore, no wave-like interference effects are very evident for light. Finally, it was long known, as we have mentioned, that sound waves were compressional waves in air. If light is a wave, just what is waving? It clearly isn’t just air, because light reaches us from the sun, and indeed from stars, and we know the air doesn’t stretch that far, or the planets would long ago have been slowed down by air resistance.
Despite all these objections, it was established around 1800 that light is
in fact some kind of wave. The
reason this fact had gone undetected for so long was that the wavelength is really
short, about one fifty-thousandth of an inch. In contrast, the shortest wavelength sound
detectable by humans has a wavelength of about half an inch. The fact that light travels in straight lines
is in accord with observations on sound that the higher the frequency (and
shorter the wavelength) the greater the tendency to go in straight lines. Similarly, the interference patterns mentioned
above for sound waves or ripples on a pond vary over distances of the same sort
of size as the wavelengths involved. Patterns like that would not normally be
noticeable for light because they would be on such a tiny scale. In fact, it turns out, there are ways
to see interference effects with light. A
familiar example is the many colors often visible in a soap bubble. These come about because looking at a soap
bubble you see light reflected from both
sides of a very thin film of water—a
thickness that turns out to be comparable to the wavelength of light. The light reflected from the lower boundary
has to go a little further to reach your eye, so that light wave must wave an
extra time or two before getting to your eye compared with the light reflected
from the top of the film. What you
actually see is the sum of the light reflected from the top and
that reflected from the bottom. Thinking
of this now as the sum of two sets of waves, the light will be bright if the
crests of the two waves arrive  together,
dim if the crests of waves reflected from the top layer arrive
simultaneously with the troughs of waves reflected from the bottom
layer. Which of these two possibilities
actually occurs for reflection from a particular bit of the soap film depends
on just how much further the light reflected from the lower surface has to
travel to reach your eye compared with light from the upper surface, and that
depends on the angle of reflection and the thickness of the film. Suppose now we shine white light on the
bubble. White light is made up of all
the colors of the rainbow, and these different colors have different
wavelengths, so we see colors reflected, because for a particular film, at a
particular angle, some colors will be reflected brightly (the crests will
arrive together), some dimly, and we will see the ones that win.
together,
dim if the crests of waves reflected from the top layer arrive
simultaneously with the troughs of waves reflected from the bottom
layer. Which of these two possibilities
actually occurs for reflection from a particular bit of the soap film depends
on just how much further the light reflected from the lower surface has to
travel to reach your eye compared with light from the upper surface, and that
depends on the angle of reflection and the thickness of the film. Suppose now we shine white light on the
bubble. White light is made up of all
the colors of the rainbow, and these different colors have different
wavelengths, so we see colors reflected, because for a particular film, at a
particular angle, some colors will be reflected brightly (the crests will
arrive together), some dimly, and we will see the ones that win.
If Light is a Wave, What is Waving?
Having established that light is a wave, though, we still haven’t answered one of the major objections raised above. Just what is waving? We discussed sound waves as waves of compression in air. Actually, that is only one case—sound will also travel through liquids, like water, and solids, like a steel bar. It is found experimentally that, other things being equal, sound travels faster through a medium that is harder to compress: the material just springs back faster and the wave moves through more rapidly. For media of equal springiness, the sound goes faster through the less heavy medium, essentially because the same amount of springiness can push things along faster in a lighter material. So when a sound wave passes, the material—air, water or solid—waves as it goes through. Taking this as a hint, it was natural to suppose that light must be just waves in some mysterious material, which was called the aether, surrounding and permeating everything. This aether must also fill all of space, out to the stars, because we can see them, so the medium must be there to carry the light. (We could never hear an explosion on the moon, however loud, because there is no air to carry the sound to us.) Let us think a bit about what properties this aether must have. Since light travels so fast, it must be very light, and very hard to compress. Yet, as mentioned above, it must allow solid bodies to pass through it freely, without aether resistance, or the planets would be slowing down. Thus we can picture it as a kind of ghostly wind blowing through the earth. But how can we prove any of this? Can we detect it?
Detecting the Aether Wind: the Michelson-Morley Experiment
Detecting the aether wind was the next challenge Michelson set himself after his triumph in measuring the speed of light so accurately. Naturally, something that allows solid bodies to pass through it freely is a little hard to get a grip on. But Michelson realized that, just as the speed of sound is relative to the air, so the speed of light must be relative to the aether. This must mean, if you could measure the speed of light accurately enough, you could measure the speed of light travelling upwind, and compare it with the speed of light travelling downwind, and the difference of the two measurements should be twice the windspeed. Unfortunately, it wasn’t that easy. All the recent accurate measurements had used light travelling to a distant mirror and coming back, so if there was an aether wind along the direction between the mirrors, it would have opposite effects on the two parts of the measurement, leaving a very small overall effect. There was no technically feasible way to do a one-way determination of the speed of light.
At this point, Michelson had a very clever idea for detecting the aether wind. As he explained to his children (according to his daughter), it was based on the following puzzle:
Suppose we have a river of width w (say, 100 feet), and two swimmers who both swim at the same speed v feet per second (say, 5 feet per second). The river is flowing at a steady rate, say 3 feet per second. The swimmers race in the following way: they both start at the same point on one bank. One swims directly across the river to the closest point on the opposite bank, then turns around and swims back. The other stays on one side of the river, swimming upstream a distance (measured along the bank) exactly equal to the width of the river, then swims back to the start. Who wins?
Let’s consider first the swimmer going upstream and back. Going 100 feet upstream, the speed relative to the bank is only 2 feet per second, so that takes 50 seconds. Coming back, the speed is 8 feet per second, so it takes 12.5 seconds, for a total time of 62.5 seconds.
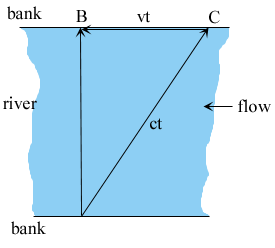
Figure 1: In time t, the swimmer has moved ct relative to the water, and been carried downstream a distance vt.
The swimmer going across the flow is trickier. It won’t do simply to aim directly for the opposite bank-the flow will carry the swimmer downstream. To succeed in going directly across, the swimmer must actually aim upstream at the correct angle (of course, a real swimmer would do this automatically). Thus, the swimmer is going at 5 feet per second, at an angle, relative to the river, and being carried downstream at a rate of 3 feet per second. If the angle is correctly chosen so that the net movement is directly across, in one second the swimmer must have moved four feet across: the distances covered in one second will form a 3,4,5 triangle. So, at a crossing rate of 4 feet per second, the swimmer gets across in 25 seconds, and back in the same time, for a total time of 50 seconds. The cross-stream swimmer wins. This turns out to true whatever their swimming speed. (Of course, the race is only possible if they can swim faster than the current!)
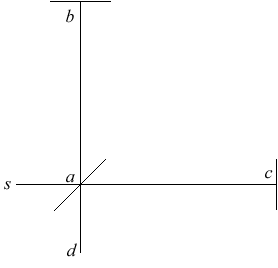
Figure 2: This diagram is from the original paper. The source of light is at s, the 45 degree line is the half-silvered mirror, b and c are mirrors and d the observer.
Michelson’s great idea was to construct an exactly similar race for pulses of light, with the aether wind playing the part of the river. The scheme of the experiment is as follows: a pulse of light is directed at an angle of 45 degrees at a half-silvered, half transparent mirror, so that half the pulse goes on through the glass, half is reflected. These two half-pulses are the two swimmers. They both go on to distant mirrors which reflect them back to the half-silvered mirror. At this point, they are again half reflected and half transmitted, but a telescope is placed behind the half-silvered mirror as shown in the figure so that half of each half-pulse will arrive in this telescope. Now, if there is an aether wind blowing, someone looking through the telescope should see the halves of the two half-pulses to arrive at slightly different times, since one would have gone more upstream and back, one more across stream in general. To maximize the effect, the whole apparatus, including the distant mirrors, was placed on a large turntable so it could be swung around.
We have an animation, including the aether wind and the rotating turntable, here!
Let us think about what kind of time delay we expect to find between the arrival of the two half-pulses of light. Taking the speed of light to be miles per second relative to the aether, and the aether to be flowing at miles per second through the laboratory, to go a distance miles upstream will take seconds, then to come back will take seconds. The total roundtrip time upstream and downstream is the sum of these, which works out to be which can also be written
Now, we can safely assume the speed of the aether is much less than the speed of light, otherwise it would have been noticed long ago, for example in timing of eclipses of Jupiter’s satellites. This means is a very small number, and we can use some handy mathematical facts to make the algebra a bit easier. First, if is very small compared to is very close to (You can check it with your calculator.) Another fact we shall need in a minute is that for small the square root of is very close to
Putting all this together,
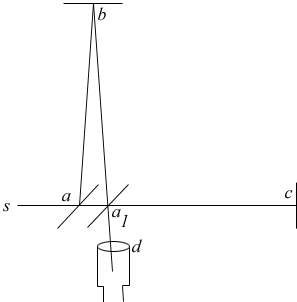
Figure 3 This is also from the original paper, and shows the expected path of light relative to the aether with an aether wind blowing.
Now, what about the cross-stream time? The actual cross-stream speed must be figured out as in the example above using a right-angled triangle, with the hypoteneuse equal to the speed the shortest side the aether flow speed and the other side the cross-stream speed we need to find the time to get across. From Pythagoras’ theorem, then, the cross-stream speed is
Since this will be the same both ways, the roundtrip cross-stream time will be
This can be written in the form
where the two successive approximations, valid for are and
Therefore
Looking at the two roundtrip times at the ends of the two paragraphs above, we see that they differ by an amount
Now, is just the time the light would take if there were no aether wind at all, say, a few millionths of a second. If we take the aether windspeed to be equal to the earth’s speed in orbit, for example, is about 1/10,000, so is about 1/100,000,000.
This means the time delay between the pulses reflected from the different mirrors reaching the telescope is about one-hundred-millionth of a few millionths of a second.
It seems completely hopeless that such a short time delay could be detected. However, this turns out not to be the case, and Michelson was the first to figure out how to do it. The trick is to use the interference properties of the light waves. Instead of sending pulses of light, as we discussed above, Michelson sent in a steady beam of light of a single color. This can be visualized as a sequence of ingoing waves, with a wavelength one fifty-thousandth of an inch or so. Now this sequence of waves is split into two, and reflected as previously described. One set of waves goes upstream and downstream, the other goes across stream and back. Finally, they come together into the telescope and the eye. If the one that took longer is half a wavelength behind, its troughs will be on top of the crests of the first wave, they will cancel, and nothing will be seen. If the delay is less than that, there will still be some dimming. However, slight errors in the placement of the mirrors would have the same effect. This is one reason why the apparatus is built to be rotated—see the animation! On turning it through 90 degrees, the upstream-downstream and the cross-stream waves change places. Now the other one should be behind. Thus, if there is an aether wind, if you watch through the telescope while you rotate the turntable, you should expect to see variations in the brightness of the incoming light.
To magnify the time difference between the two paths, in the actual experiment the light was reflected backwards and forwards several times, like a several lap race.
Michelson calculated that an aether windspeed of only one or two miles a second would have observable effects in this experiment, so if the aether windspeed was comparable to the earth’s speed in orbit around the sun, it would be easy to see. In fact, nothing was observed. The light intensity did not vary at all. Some time later, the experiment was redesigned so that an aether wind caused by the earth’s daily rotation could be detected. Again, nothing was seen. Finally, Michelson wondered if the aether was somehow getting stuck to the earth, like the air in a below-decks cabin on a ship, so he redid the experiment on top of a high mountain in California. Again, no aether wind was observed. It was difficult to believe that the aether in the immediate vicinity of the earth was stuck to it and moving with it, because light rays from stars would deflect as they went from the moving faraway aether to the local stuck aether.
The only possible conclusion from this series of very difficult experiments was that the whole concept of an all-pervading aether was wrong from the start. Michelson was very reluctant to think along these lines. In fact, new theoretical insight into the nature of light had arisen in the 1860’s from the brilliant theoretical work of Maxwell, who had written down a set of equations describing how electric and magnetic fields can give rise to each other. He had discovered that his equations predicted there could be waves made up of electric and magnetic fields, and the speed of these waves, deduced from electrostatic and magnetostatic experiments, was predicted to be 186,300 miles per second. This is, of course, the speed of light, so it was natural to assume light to be made up of fast-varying electric and magnetic fields.
But this led to a big problem: Maxwell’s equations predicted a definite speed for light, and it was the speed found by measurements. But what was the speed to be measured relative to? The whole point of bringing in the aether was to give a picture for light resembling the one we understand for sound, compressional waves in a medium. The speed of sound through air is measured relative to air. If the wind is blowing towards you from the source of sound, you will hear the sound sooner. If there isn’t an aether, though, this analogy doesn’t hold up. So what does light travel at 186,300 miles per second relative to?
There is another obvious possibility, which is called the emitter theory: the light travels at 186,300 miles per second relative to the source of the light. The analogy here is between light emitted by a source and bullets emitted by a machine gun. The bullets come out at a definite speed (the muzzle velocity) relative to the barrel of the gun. If the gun is mounted on the front of a tank, which is moving forward, and the gun is pointing forward, then relative to the ground the bullets are moving faster than they would if shot from a tank at rest. The simplest way to test the emitter theory of light, then, is to measure the speed of light emitted in the forward direction by a flashlight moving in the forward direction, and see if it exceeds the known speed of light by an amount equal to the speed of the flashlight. Actually, this kind of direct test of the emitter theory only became experimentally feasible in the nineteen-sixties. It is now possible to produce particles, called neutral pions, which decay each one in a little explosion, emitting a flash of light. It is also possible to have these pions moving forward at 185,000 miles per second when they self destruct, and to catch the light emitted in the forward direction, and clock its speed. It is found that, despite the expected boost from being emitted by a very fast source, the light from the little explosions is going forward at the usual speed of 186,300 miles per second. In the last century, the emitter theory was rejected because it was thought the appearance of certain astronomical phenomena, such as double stars, where two stars rotate around each other, would be affected. Those arguments have since been criticized, but the pion test is unambiguous. The definitive experiment was carried out by Alvager et al., Physics Letters 12, 260 (1964).
LIGO
 We
have to mention here that the most spectacular realization (so far) of Michelson's
interference techniques is the successful detection (first in 2016) of gravitational
waves by a scaled-up version of the interferometer. The basic idea is that as a
(transverse, polarized) gravitational wave passes the two arms have their
lengths slightly altered by different amounts. The tiny effect is made detectable
by having arms kilometers in length, and the beams go back and forth in the arms
many times.
We
have to mention here that the most spectacular realization (so far) of Michelson's
interference techniques is the successful detection (first in 2016) of gravitational
waves by a scaled-up version of the interferometer. The basic idea is that as a
(transverse, polarized) gravitational wave passes the two arms have their
lengths slightly altered by different amounts. The tiny effect is made detectable
by having arms kilometers in length, and the beams go back and forth in the arms
many times.
Einstein’s Answer
The results of the various aether detection experiments discussed above seem to leave us really stuck. Apparently light is not like sound, with a definite speed relative to some underlying medium. However, it is also not like bullets, with a definite speed relative to the source of the light. Yet when we measure its speed we always get the same result. How can all these facts be interpreted in a simple consistent way? We shall show how Einstein answered this question in the next lecture.