Special Relativity
Michael Fowler, UVa Physics
Galilean Relativity again
At this point in the course, we finally enter the twentieth century—Albert Einstein wrote his first paper on relativity in 1905. To put his work in context, let us first review just what is meant by “relativity” in physics. The first example, mentioned in a previous lecture, is what is called “Galilean relativity” and is nothing but Galileo’s perception that by observing the motion of objects, alive or dead, in a closed room there is no way to tell if the room is at rest or is in fact in a boat moving at a steady speed in a fixed direction. (You can tell if the room is accelerating or turning around.) Everything looks the same in a room in steady motion as it does in a room at rest. After Newton formulated his Laws of Motion, describing how bodies move in response to forces and so on, physicists reformulated Galileo’s observation in a slightly more technical, but equivalent, way: they said the laws of physics are the same in a uniformly moving room as they are in a room at rest. In other words, the same force produces the same acceleration, and an object experiencing no force moves at a steady speed in a straight line in either case. Of course, talking in these terms implies that we have clocks and rulers available so that we can actually time the motion of a body over a measured distance, so the physicist envisions the room in question to have calibrations along all the walls, so the position of anything can be measured, and a good clock to time motion. Such a suitably equipped room is called a “frame of reference”—the calibrations on the walls are seen as a frame which you can use to specify the precise position of an object at a given time. (This is the same as a set of “coordinates”.) Anyway, the bottom line is that no amount of measuring of motions of objects in the “frame of reference” will tell you whether this is a frame at rest or one moving at a steady velocity.
What exactly do we mean by a frame “at rest” anyway? This seems obvious from our perspective as creatures who live on the surface of the earth—we mean, of course, at rest relative to fixed objects on the earth’s surface. Actually, the earth’s rotation means this isn’t quite a fixed frame, and also the earth is moving in orbit at 18 miles per second. From an astronaut’s point of view, then, a frame fixed relative to the sun might seem more reasonable. But why stop there? We believe the laws of physics are good throughout the universe. Let us consider somewhere in space far from the sun, even far from our galaxy. We would see galaxies in all directions, all moving in different ways. Suppose we now set up a frame of reference and check that Newton’s laws still work. In particular, we check that the First Law holds—that a body experiencing no force moves at a steady speed in a straight line. This First law is often referred to as The Principle of Inertia, and a frame in which it holds is called an Inertial Frame. Then we set up another frame of reference, moving at a steady velocity relative to the first one, and find that Newton’s laws are o.k. in this frame too. The point to notice here is that it is not at all obvious which—if either—of these frames is “at rest”. We can, however, assert that they are both inertial frames, after we’ve checked that in both of them, a body with no forces acting on it moves at a steady speed in a straight line (the speed could be zero). In this situation, Michelson would have said that a frame “at rest” is one at rest relative to the aether. However, his own experiment found motion through the aether to be undetectable, so how would we ever know we were in the right frame?
As we mentioned in the last lecture, in the middle of the nineteenth century there was a substantial advance in the understanding of electric and magnetic fields. (In fact, this advance is in large part responsible for the improvement in living standards since that time.) The new understanding was summarized in a set of equations called Maxwell’s equations describing how electric and magnetic fields interact and give rise to each other, just as, two centuries earlier, the new understanding of dynamics was summarized in the set of equations called Newton’s laws. The important thing about Maxwell’s equations for our present purposes is that they predicted waves made up of electric and magnetic fields that moved at 3×108 meters per second, and it was immediately realized that this was no coincidence—light waves must be nothing but waving electric and magnetic fields. (This is now fully established to be the case.)
It is worth emphasizing that Maxwell’s work predicted the speed of light from the results of experiments that were not thought at the time they were done to have anything to do with light—experiments on, for example, the strength of electric field produced by waving a magnet. Maxwell was able to deduce a speed for waves like this using methods analogous to those by which earlier scientists had figured out the speed of sound from a knowledge of the density and the springiness of air.
Generalizing Galilean Relativity to Include Light: Special Relativity
We now come to Einstein’s major insight: the Theory of Special Relativity. It is deceptively simple. Einstein first dusted off Galileo’s discussion of experiments below decks on a uniformly moving ship, and restated it as :
The Laws of Physics are the same in all Inertial Frames.
Einstein then simply brought this up to date, by pointing out that the Laws of Physics must now include Maxwell’s equations describing electric and magnetic fields as well as Newton’s laws describing motion of masses under gravity and other forces. (Note for experts and the curious: we shall find that Maxwell’s equations are completely unaltered by special relativity, but, as will become clear later, Newton’s Laws do need a bit of readjustment to include special relativistic phenomena. The First Law is still o.k., the Second Law in the form F = ma is not, because we shall find the mass in this equation varies; we need to equate force to rate of change of momentum (Newton understood that, of course—that’s the way he stated the law!). The Third Law, stated as action equals reaction, no longer holds because if a body moves, its electric field, say, does not readjust instantaneously—a ripple travels outwards at the speed of light. Before the ripple reaches another charged body, the electric forces between the two will be unbalanced. However, the crucial consequence of the Third Law—the conservation of momentum when two bodies interact, still holds. It turns out that the rippling field itself carries momentum, and everything balances.)
Demanding that Maxwell’s equations be satisfied in all inertial frames has one major consequence as far as we are concerned. As we stated above, Maxwell’s equations give the speed of light to be 3×108 meters per second. Therefore, demanding that the laws of physics are the same in all inertial frames implies that the speed of any light wave, measured in any inertial frame, must be 3×108 meters per second.
This then is the entire content of the Theory of Special Relativity: the Laws of Physics are the same in any inertial frame, and, in particular, any measurement of the speed of light in any inertial frame will always give 3×108 meters per second.
You Really Can’t Tell You’re Moving!
Just as Galileo had asserted that observing gnats, fish and dripping bottles, throwing things and generally jumping around would not help you to find out if you were in a room at rest or moving at a steady velocity, Einstein added that no kind of observation at all, even measuring the speed of light across your room to any accuracy you like, would help find out if your room was “really at rest”. This implies, of course, that the concept of being “at rest” is meaningless. If Einstein is right, there is no natural rest-frame in the universe. Naturally, there can be no “aether”, no thin transparent jelly filling space and vibrating with light waves, because if there were, it would provide the natural rest frame, and affect the speed of light as measured in other moving inertial frames as discussed above.
So we see the Michelson-Morley experiment was doomed from the start. There never was an aether wind. The light was not slowed down by going “upstream”—light always travels at the same speed, which we shall now call c,
c = 3×108 meters per second
to save writing it out every time. This now answers the question of what the speed of light, c, is relative to. We already found that it is not like sound, relative to some underlying medium. It is also not like bullets, relative to the source of the light (the discredited emitter theory). Light travels at c relative to the observer, since if the observer sets up an inertial frame (clocks, rulers, etc.) to measure the speed of light he will find it to be c. (We always assume our observers are very competent experimentalists!)
Truth and Consequences
The Truth we are referring to here is the seemingly innocuous and plausible sounding statement that all inertial frames are as good as each other—the laws of physics are the same in all of them—and so the speed of light is the same in all of them. As we shall soon see, this Special Theory of Relativity has some surprising consequences, which reveal themselves most dramatically when things are moving at relative speeds comparable to the speed of light. Einstein liked to explain his theory using what he called “thought experiments” involving trains and other kinds of transportation moving at these speeds (technically unachievable so far!), and we shall follow his general approach.
To begin with, let us consider a simple measurement of the speed of light carried out at the same time in two inertial frames moving at half the speed of light relative to each other. The setup is as follows: on a flat piece of ground, we have a flashlight which emits a blip of light, like a strobe. We have two photocells, devices which click and send a message down a wire when light falls on them. The photocells are placed 10 meters apart in the path of the blip of light, they are somehow wired into a clock so that the time taken by the blip of light to travel from the first photocell to the second, in other words, the time between clicks, can be measured. From this time and the known distance between them, we can easily find the speed of the blip of light.
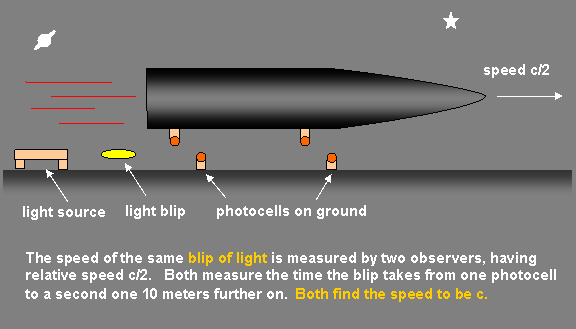
Meanwhile, there is another observer, passing overhead in a spaceship traveling at half the speed of light. She is also equipped with a couple of photocells, placed 10 meters apart on the bottom of her spaceship as shown, and she is able to measure the speed of the same blip of light, relative to her frame of reference (the spaceship). The observer on the spaceship will measure the blip of light to be traveling at c relative to the spaceship, the observer on the ground will measure the same blip to be traveling at c relative to the ground. That is the unavoidable consequence of the Theory of Relativity.
(Note: actually the picture above is not quite the way it would really look. As we shall find, objects moving at relativistic speeds are contracted, and this combined with the different times light takes to reach the eye from different parts of the ship would change the ship’s appearance. But this does not affect the validity of the statements above.)