Multiparticle Wavefunctions and Symmetry

Michael Fowler, University of Virginia

Two Electrons in a One Dimensional Well

So far, we have used Schrödinger’s equation to see how a single particle, usually an electron, behaves in a variety of potentials. If we are going to think about atoms other than hydrogen, it is necessary to extend the Schrödinger equation so that it describes more than one particle.

As a simple example of a two particle system, let us consider two electrons confined to the same one-dimensional infinite square well,

$\begin{array}{c} V (x) = \infty, x < - L / 2, \\ V (x) = 0, - L / 2 \leq x \leq L / 2, \\ V (x) = \infty, L / 2 < x . \end{array}$

To make things even simpler, let us assume that the electrons do not interact with each other $—$ we switch off their electrostatic repulsion. Then by analogy with our construction of the Schrödinger equation for a single electron, we write

$- \frac{ℏ^{2}}{2 m} \frac{\partial^{2} ψ (x_{1}, x_{2}, t)}{\partial x_{1}^{2}} - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} ψ (x_{1}, x_{2}, t)}{\partial x_{2}^{2}} = E ψ (x_{1}, x_{2}, t)$

inside the well, with the wave function going to zero for $x_{1}$ or $x_{2}$ equal to $\pm L / 2.$

On looking at this equation, we see it is the same as the Schrödinger equation for a single electron in a two dimensional square well, and so can be solved in the same way, by separation of variables. For example, the wave function we plotted for the two dimensional rectangular well is in the square case:

$ψ_{(2, 3)} (x_{1}, x_{2}, t) = A \sin (2 π x_{1} / L) \cos (3 π x_{2} / L) e^{- i E t / ℏ}$

has the same energy

$E = \frac{ℏ^{2}}{2 m} \frac{π^{2}}{L^{2}} (2^{2} + 3^{2})$

as the physically distinct wavefunction:

$ψ_{(3, 2)} (x_{1}, x_{2}, t) = A \sin (2 π x_{2} / L) \cos (3 π x_{1} / L) e^{- i E t / ℏ} .$

Interpreting the Wavefunction

We have already discussed how the above wavefunctions are to be interpreted if they are regarded as two-dimensional wavefunctions for a single electron: ${| ψ (x_{1}, x_{2}) |}^{2} d x_{1} d x_{2}$ is the probability of finding the electron in a small area $d x_{1} d x_{2}$ at $(x_{1}, x_{2}) .$

The natural extension of this interpretation to two electrons is to assume now ${| ψ (x_{1}, x_{2}) |}^{2} d x_{1} d x_{2}$ is the joint probability of finding electron 1 in a small line length $d x_{1}$ at position $x_{1},$ and at the same time finding electron 2 in a small length $d x_{2}$ at $x_{2} .$

This, however, leads to a real problem. Consider the wavefunction

$ψ_{(2, 3)} (x_{1}, x_{2}, t) = A \sin (2 π x_{1} / L) \cos (3 π x_{2} / L) e^{- i E t / ℏ}$

again. Let us now take specific points, $x_{1} = 0, x_{} = L / 4.$ Then the probability of finding electron 1 in an infinitesimal interval at $x_{1}$ and electron 2 similarly at $x_{2}$ is zero, because $ψ$ is zero at $x_{1} = 0.$ On the other hand, the probability of finding electron 2 at $x_{1} (= 0)$ and electron 1 at $x_{2} (= L / 4)$ is not zero.

The problem is this: the electrons are identical (we assume their spins point the same way). We can’t tell which is which, and nobody else can either. The indistinguishability of elementary particles is not like that of apparently identical macroscopic objects, where one could always place some tiny mark. There is no way to mark an electron. This means, though, that the best we can do is to talk about the probability of finding one electron at $x_{1}$ and another at $x_{2},$ we cannot specify which electron we find where. Therefore, any alleged wave function that gives different probabilities for finding electron 1 at $x_{1},$ 2 at $x_{2}$ and finding 2 at $x_{1},$ 1 at $x_{2}$ is not physically meaningful.

That is to say, a wave function describing two identical particles must have a symmetric probability distribution

${| ψ (x_{1}, x_{2}) |}^{2} = {| ψ (x_{2}, x_{1}) |}^{2} .$

This is definitely not the case with our function $ψ_{(2, 3)} (x_{1}, x_{2}),$ , so although it is a solution to the two particle Schrödinger equation, it is not a physically meaningful wave function for two particles in a one-dimensional box.

In fact, this is not difficult to fix $—$ recall that the function $ψ_{(3, 2)} (x_{1}, x_{2})$ has the same energy, and in fact just corresponds to the two particles being switched around, that is to say, $ψ_{(3, 2)} (x_{1}, x_{2}) = ψ_{(2, 3)} (x_{2}, x_{1}) .$

It follows that the symmetric function

$ψ_{(2, 3)}^{S} (x_{1}, x_{2}) = \frac{1}{\sqrt{2}} (ψ_{(2, 3)} (x_{1}, x_{2}) + ψ_{(2, 3)} (x_{2}, x_{1}))$

and the antisymmetric function

$ψ_{(2, 3)}^{S} (x_{1}, x_{2}) = \frac{1}{\sqrt{2}} (ψ_{(2, 3)} (x_{1}, x_{2}) - ψ_{(2, 3)} (x_{2}, x_{1}))$

are both solutions to Schrödinger’s equation for the energy $E,$ and both satisfy the requirement ${| ψ (x_{1}, x_{2}) |}^{2} = {| ψ (x_{2}, x_{1}) |}^{2}$ necessary for identical particles, so these are the appropriate candidate wave functions for the two particles in the one-dimensional box.

Bosons, Fermions and the Pauli Exclusion Principle

It turns out that both symmetric and antisymmetric wavefunctions arise in nature in describing identical particles. In fact, all elementary particles are either fermions, which have antisymmetric multiparticle wavefunctions, or bosons, which have symmetric wave functions. Electrons, protons and neutrons are fermions; photons, $α$ -particles and helium atoms are bosons.

It is important to realize that this requirement of symmetry of the probability distribution, arising from the true indistinguishability of the particles, has a large effect on the probability distribution, and, furthermore, the effect is very different for fermions and bosons. The simplest way to see this is just to plot ${| ψ (x_{1}, x_{2}) |}^{2}$ for the symmetric and for the antisymmetric wave functions, and compare them.

For the symmetric case, the probability distribution (unnormalized) looks like:

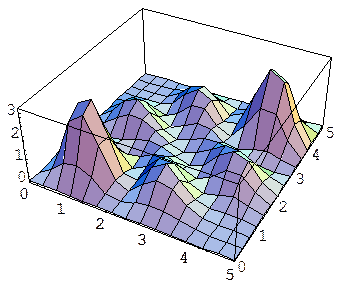
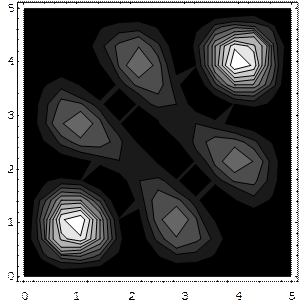
(The graytone figure is a contour map.)

The main point to note here is that the highest joint probability is that of finding the two particles close together, near (1,1) and (4,4). (These actual points depend on the wave function we chose initially, of course).

Now look at the antisymmetric case:

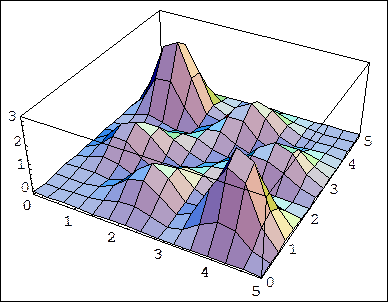
The difference is dramatic. For the antisymmetric wave function, the particles are most likely to be found far away from each other. In fact, there is zero probability that they will be found at the same spot, because if $ψ (x_{1}, x_{2}) = - ψ (x_{2}, x_{1}),$ obviously $ψ (x, x) = 0.$ A more general statement is that two fermions cannot be in the same quantum state, because if they were, the wave function would be of the symmetric form $f (x_{1}) f (x_{2}),$ and could not be antisymmetrized.

This is the Pauli Exclusion Principle $—$ it is the basis of the periodic table, and consequently of almost everything else.

We should perhaps emphasize that these wave functions were calculated with the electrostatic repulsion between the electrons switched off. That is not what is keeping the electrons apart, although it will increase the separation if it is included. We should also warn against a simple classical picture of the Pauli principle, the thought that two things can’t be in the same place, after all, so perhaps it’s no surprise two electrons can’t be in the same state. Two electrons can be in the same identical space wave function provided that their spins point in opposite ways. Furthermore, two bosons can be in the same state, and although that is perhaps reasonable sounding for photons, it is equally true for heavy atoms. In Bose-Einstein Condensation, a large number of atoms occupy the same quantum state. This happens in liquid Helium⁴ below about two kelvin, it becomes a superfluid and flows without friction. Furthermore, BE condensation of laser cooled collections of large atoms in a trap is now fairly routine.

previous home next PDF