Solution of the diffusion equation

Dimensional analysis can also be used to solve certain types of partial differential equations. If this seems too good to be true, it isn't. Here we will concentrate on the solution of the diffusion equation; we will encounter this equation many times in the remainder of the course, so it will be useful to work out some of its properties now.

We'll start by deriving the one-dimensional diffusion, or heat, equation. Let represent the temperature of a metal bar at a point x at time t (I'll use to avoid confusion with the symbol for the dimension of time, T). The first step is the derivation of a continuity equation for the heat flow in the bar. Let the bar have a cross sectional area A, so that the infinitesimal volume of the bar between x and is . The quantity of heat contained in this volume is , with the specific heat at constant pressure per unit volume; it has dimensions . In a time interval dt this heat changes by an amount due to the change in temperature. This change in the heat must come from somewhere, and is the result of a flux of heat q(x,t) through the area A (q is the heat flowing through a unit area per unit time). Into the left side of the volume an amount of heat q A dt flows in a time dt; on the right hand side of the volume a quantity flows out in a time dt, so that the net accumulation of heat in the volume is . Equating the two expressions for the rate of change of the heat in the volume , we find

 

which is the equation of continuity. It is a mathematical expression of the conservation of heat in the infinitesimal volume . We supplement this with a phenomenological law of heat conduction, known as Fourier's law: the heat flux is proportional to the negative of the local temperature gradient (heat flows from a hot reservoir to a cold reservoir):

 

with the thermal conductivity of the metal bar. The thermal conductivity is usually measured in units of , and has dimensions . See the Table on p. 118 of the PQRG for the thermal conductivities of some materials. Combining Eqs. (1.22) and (1.23), we obtain the diffusion equation (often called the heat equation)

 

where is the thermal diffusivity of the metal bar; it has dimensions , as it should. Eq. (1.24) is the diffusion equation for heat. The diffusion equation will appear in many other contexts during this course. It usually results from combining a continuity equation with an empirical law which expresses a current or flux in terms of some local gradient.

Suppose that the bar is very long, so that we can consider the idealized case of an infinite bar. At an initial time t=0, we add an amount of heat H (with dimensions ) at some point of the bar, which we will arbitrarily call x=0. We could do this, for instance, by briefly holding a match to the bar. The heat is conserved at all times, so that

 

How does this heat diffuse away from x=0 as a function of time t; i.e., what is ? We first identify the important parameters. The temperature certainly depends upon x, t, and the diffusivity D; we see from Eq. (1.25) that it also depends upon the initial conditions through the combination . What are the dimensions? We have [x]=L, [t]=T, , and , so that n=4. These dimensions are not independent, for the quantity is dimensionless, so that k=3. We will choose as our independent quantities (t,D,Q). Now express in terms of these variables:

 

We find

 

which has the solution a=-1/2, b=-1/2, c=1. Therefore, dimensional analysis tells us that the solution of the diffusion equation is of the form

 

with a function which we still need to determine. The important point is that is only a function of the combination , and not x and t separately. To determine , let's introduce the dimensionless variable . Now use the chain rule to calculate various derivatives of :

 

 

 

Substituting Eqs. (1.30) and (1.31) into the diffusion equation (1.24), and canceling various factors, we obtain a differential equation for ,

 

Dimensional analysis has reduced the problem from the solution of a partial differential equation in two variables to the solution of an ordinary differential equation in one variable! The normalization condition, Eq. (1.25), becomes in these variables

 

You might think that Eq. (1.32) is hard to solve; however, it turns out that it is an exact differential,

 

which we can integrate once to obtain

 

However, since any physically reasonable solution would have both and as , the integration constant must be zero. We now need to solve a first order differential equation, which we do by dividing Eq. (1.35) by , multiplying by dz, and integrating, with the result that , or

 

with C a constant. To determine C, we use the normalization condition, Eq, (1.33):

 

where the integral (known as a Gaussian integral) can be found in integral tables. Therefore . Returning to our original variables, we have

 

This is the complete solution for the temperature distribution in a one-dimensional bar due to a point source of heat. Here are pictures:

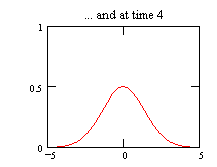
Click here to see an animation (controlled by mouse buttons) of the one-dimensional diffusion process described by eq. (1.38). The animation starts at some arbitrary time t₀ (zero time corresponds to an infinitely sharp peak) and ends at 25t₀, and x is in units of the square root of Dt₀.