To obtain the equation of motion for a fluid we appeal to Newton's Second Law--the mass of a fluid element times its acceleration is equal to the net force acting on that fluid element. If we take an element of unit volume, then we have
where 
is the force per unit volume on a fluid element. This force
may have several contributions. The first is the ``internal'' force which is
due to viscous dissipation, which we will ignore for right now. The second
set are ``body forces'' which act throughout the volume of the fluid, such
as the gravitational force. The third force is due to pressure gradients
within the fluid. To see how this works, consider a cube of fluid, with
dimensions 
, 
, and 
, as shown in Fig. 2.6.
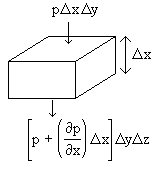
Figure 2.6: Derivation of the force on a fluid
element due to pressure gradients.
, while
the force on the bottom face is 
; subtracting, we see that the net force in the x-direction is 
, so the
pressure per unit volume is 
. Repeating for the y
and z directions, we find the net force per unit volume 
. Therefore, if we ignore viscosity and gravity for the moment, we
have
Now comes the tricky part. What is the acceleration of the fluid? We want
the acceleration of a particular element of the fluid; the coordinates of
this fluid element change in time as the fluid flows. In a time interval 
, the x-coordinate changes by 
, the y-coordinate
by 
, and the z-coordinate by 
. The velocity
then becomes
To calculate the acceleration, we need to find the rate of change of the velocity:
We see that the acceleration is not simply 
. The reason for this is that even if 
, so that the velocity at a given point is not changing, that
doesn't mean that a fluid element is not accelerating. A good example is
circular flow in a bucket. If the flow is steady, then at a point in the
bucket , even though a fluid element in
the bucket is experiencing a centripetal acceleration. The term 
is nonlinear, and is the source of all of the
difficulties in fluid mechanics. Pulling together all of the pieces, we have
for our equation of motion
This is known as Euler's equation . This equation and the equation of continuity are the governing equations of nonviscous fluid flow.
For an incompressible fluid, the Euler equation can be written in a somewhat different form which is often useful for applications. We use the following identity from vector calculus:
[see the PQRG, p. 161, next to last equation]. Next we use 
, and the fact that the fluid is incompressible so that 
is
constant, to rewrite Eq. (2.20) as
This is still a complicated equation, but it has interesting consequences. If we apply Ñ× to both sides of this equation, and remenber that the curl of a gradient is zero, we obtain an equation that tells us how the vorticity moves:
¶w/¶t + Ñ×(w×v) = 0.
In particular, this equation shows that w remains zero at all times if it is zero initially. It also it allows us to check if some w can stay fixed in time and produce a steady flow. 
