Let's now consider one particularly simple nonviscous flow, the irrotational flow of a fluid around a cylinder. This problem will demonstrate how some fluid mechanics problems are solved, and brings out an important paradox in the theory of nonviscous flow.
We consider a cylinder of radius R, with an imposed flow of velocity 
far from the cylinder--see Fig. 2.7.
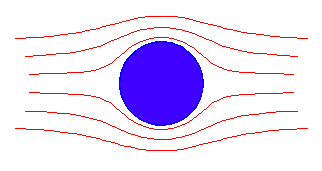
Figure 2.7: Flow past a cylinder
.
What is the equation for 
? Since the flow is irrotational, 
, and from vector calculus we know that this
implies that may be written as the gradient of some scalar
function: 
. If the fluid is also incompressible,
then 
, so that
The potential function 
is a
solution of Laplace's equation, which should be familiar to those of
you who have studied advanced electrostatics. In radial coordinates
Laplace's equation is
In terms of the boundary condition at infinity is 
; in radial coordinates 
, so this
becomes
At the surface of the cylinder we have
The strategy is that we solve Laplace's equation for , and then calculate the velocity field
from the potential.
1 To do this we
first need to realize that in order to satisfy the boundary condition at
infinity, 
; therefore, we set
Substituting this into Laplace's equation, Eq. (2.29), we obtain a differential equation for f:
To solve this equation, we'll guess the solution 
, and
see if we can find an appropriate value of 
. Substituting, we find 
, so that our solution is
Using the boundary condition at infinity, we see that A=-U; applying the
boundary condition at the surface of the cylinder, we find 
, so our
final solution is
The components of the velocity are
The streamlines in this case are symmetric on the upstream and downstream sides of the cylinder.
How does the pressure vary around the cylinder? First, the square of the velocity on the surface of the cylinder is
We can now use Bernoulli's equation; since the flow is irrotational, the
constant is the same everywhere in the fluid. In particular, at infinity the
constant is 
, where 
is the ambient pressure
(which we can choose to be zero without any loss of generality). The
pressure on the surface of the cylinder is then
From the pressure we can calculate the net force acting on the cylinder.
First, recall that the pressure at the surface of the cylinder is the force
per unit area acting on the cylinder; therefore the force 
acting
upon an element of the cylinder of surface area dS is 
, where 
is a unit vector normal to the surface,
and the minus sign indicates that this force acts inward. Next, we
integrate this over the entire surface of the cylinder to find the net
force:
For the cylinder, 
, with z along the axis of the
cylinder. The unit vector depends upon the angle 
as 
. Then the x and y
components of the force are
where 
is the length of the cylinder in the z-direction. If we now
substitute our expression for the pressure distribution on the surface of
the cylinder, Eq. 2.39, into our expressions for the drag and the
lift, Eqs. 2.41 and 2.42, and perform the integration,
we find that 
! Although we have performed an explicit
calculation for a cylinder, the result is more general: irrotational
flow of a nonviscous fluid about an object produces no drag on the object.
This peculiar result is known as d'Alembert's paradox.
Physically, the fact that the drag is zero is due to the symmetry of the
pressure field about the cylinder--the fluid is pushing as hard on the
upstream side of the cylinder as on the downstream side, so there are no
unbalanced forces which would lead to drag. Whether or not this is
paradoxical is a matter of opinion. If there were a drag on the cylinder,
how would the energy be dissipated in a nonviscous fluid? To really
understand drag, we need to go beyond the nonviscous approximation and treat
real fluids.
Footnote
1 In electrostatics j would be the electrostatic potential, and the electric field would be given by E = - Ñj.
