Streamlines and streamtubes

In problems involving electric or magnetic fields we visualize the fields by introducing field lines (often called lines of force), which have the properties that (1) they are everywhere tangent to the field vectors, and (2) the density of the field lines is proportional to the magnitude (strength) of the field. We can use the same method to visualize the velocity field by introducing streamlines, which have the following properties:

• a tangent to a streamline at a point is in the direction of the fluid velocity at that point;
• the density of streamlines in the vicinity of a point is proportional to the magnitude of the velocity at that point;
• the streamlines cannot intersect except at a point of zero velocity, otherwise the velocity would not be uniquely determined at that point.

A streamtube is a tubular region of fluid surrounded by streamlines. Since streamlines don't intersect, the same streamlines pass through a streamtube at all points along its length. Let's take two cross-sections of a streamtube, with cross-sectional areas and (see Fig. 2.4).   

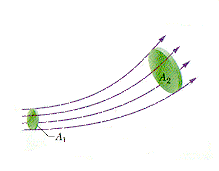
Figure 2.4: A streamtube in a fluid.

If these areas are made small enough then the fluid velocities across the cross-sections will be constant; let's call the speeds and (the directions of the velocities being perpendicular to the cross-sections). The rate at which mass is entering the streamtube is ; the rate at which it is leaving is . If the mass inside the streamtube is not changing with time, so that the fluid is either incompressible or in steady-state, we have

 

If, in addition, the fluid is incompressible, then , and we have

 

so that the fluid speed increases when the cross-sectional area of the streamtube decreases. If this seems counter-intuitive, the following analogy might help. You drive down a four lane highway, and due to construction one lane on your side has been closed. The traffic crawls toward the point where the lane has been closed, with cars haphazardly merging into your lane. You finally hit the single lane, and whiz through the construction area. The cross-sectional area has decreased, and your speed has increased.