![]()
- (a)
- For a simple cross section of a rod or beam, sketch the trace of the neutral plane and indicate the coordinate y to be used in the above formula. Justify Feynman's assertion that I is the moment of inertia of a slice with unit mass per unit area (about which axis?).
- (b)
- Compute I for a beam having rectangular cross section of sides a and b. If b = 2a, how much more force is required to bend the beam in the easy direction than in the other?
- (c)
- Compute I for a tube having inner radius a, outer radius b. The
math is easier if you show first that, in this case,
Is a hollow tube harder to bend than a solid cylinder of the same weight and length?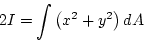
http://www.phys.virginia.edu/classes/109N/lectures/scaling.html
and answer the following:
- (a)
- Exactly how much bigger must the rope be to hold up the chandelier that is eight times heavier? How much bigger must the radius be, how much bigger the cross-section?
- (b)
- A marble column laying on the ground has a tendency to break if it supported at two points only. Which is more likely to break, a small column or a larger one of the same shape? If the small column has length l and radius r and the big column has length L, what must its radius be to make it as unlikely to break as the small column? (The answer is in Two New Sciences.)
- (c)
- If the size of a building is doubled, all lengths being doubled, how much stronger must the materials be to make the bigger building as safe as the original? Assume that the strength can be increased without changing the density.
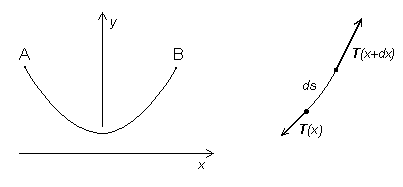
- (a)
- Consider a small segment of the rope, as shown, which has a mass dm. Show that
What is the meaning of T1? Why is it a constant?
(1) - (b)
- Let
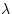 be the mass per unit length of the rope, so that
be the mass per unit length of the rope, so that
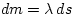 , with dm the arclength of the segment. By using your
result from part (a), show that the shape y(x) satisfies the differential
equation
, with dm the arclength of the segment. By using your
result from part (a), show that the shape y(x) satisfies the differential
equation

(2) - (c)
- This differential equation is nonlinear, and generally difficult to
solve; the solution is
Substitute this trial solution into the differential equation, Eq. 2, and verify that it is indeed a solution, if a is chosen properly. This solution is known as the catenary.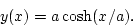
(3) - (d)
- Suppose you want to build an arch whose members are only in
compression. What shape should it take? Why? This is the shape of the famous
Gateway Arch in St. Louis.
- (a)
- The length l versus the thickness d of the humerus for different
antelopes is plotted on a log-log scale in the book On Size and Life.
From the plot we see that
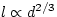 . Derive this relation from what
you know about elasticity and buckling.
. Derive this relation from what
you know about elasticity and buckling.
- (b)
- In old horror movies Godzilla is depicted as an overgrown iguana, the size of a Tokyo skyscraper. Is this consistent with allometric requirements?