Lecture 1, Jan 15, 98
Review of electrostatics: Coulomb's law, relation of field to potential, E = - ÑV. Charge distribution on insulators and conductors.
Assigned reading: Bloomfield, section 11.1
Assigned problem set 1 (field enhancement at a bump)
References:
Lecture 2, Jan 20
Continued review of electrostatics:
Ñ × E = 0,
Ñ · E = r/e0 (or
Ñ · E = 4pr in gaussian units)
and Poisson's equation Ñ2V = - r/e0 (or
Ñ2V = - 4pr in gaussian units).
In charge-free space 
(Laplace's equation). Analogy of electric field to fluid velocity for an
incompressible, non-viscous fluid. Dipole moment; field of a dipole, force on a dipole (proportional to field gradient). Induced dipole on a conducting sphere and on a molecule. Electrical discharges.
Demos: discharges from domes and a sharp point; Jacob's ladder (effect of previous discharges)
References: same as last lecture.
Problem session 1
Given hints on solving problem set 1, using MAPLE to do the plots. Handed out MAPLE help sheet.
Lecture 3, Jan 22
Demos: precipitating smoke particles; shown ''insides'' of electrostatic air cleaner.
Assigned problem set 2 (engineering of electrostatic precipitator; energy and wavelength of emitted photon)
Capacitance and capacitors. Review of quantum mechanics: action, phase,
sum over all possible paths with a phase factor, uncertainty principle,
spin and the Pauli exclusion principle, plane wave solution of
the time-dependent Schrodinger equation,
E = hf =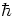 
w and
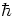p = k.
What is quantized? Action is quantized in units of h;
as a consequence, other quantities are quantized too, but not so simply.
What is action? It is a quantity with dimensions ML2T-1;
it can be energy × time, or momentum × length. Angular momentum has the same dimensions as action
and is simply quantized in units of .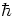
What is spin? It is something like the internal angular momentum of an elementary particle.
However, electrons (and quarks) have sp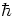in /2, which is weird.
Photons have spin 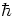. One often says that electrons have spin 1/2 and photons
have spin 1.
What is the Pauli exclusion principle? Read about it in Serway, page 860, as it applies
to electrons. Actually, it applies to all elementary particles with spin 1/2 (called fermions) and is
mysteriously related to their unusual spin. It also applies to composite particles with half-integer spin
(1/2, 3/2, etc.).
References:
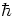, so that some formulas look a little different. Physics
articles today almost always use 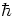, unless they use "atomic units" in
which 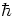is set equal to 1. See last semester's
lecture on
atomic units.Lecture 4, Jan 27
- Particle in a box (one dimensional); obtained energy eigenvalues
where n is a positive integer. Plotted eigenfunctions 
for n=1,2,3. One can write 
where 
is the ground state
energy.
- Harmonic oscillator; eigenvalues
where n is a positive integer or zero. One can write 
where 
is the ground
state energy, also called the zero-point energy.
- Classical Kepler problem (hydrogen atom, neglecting spin and relativistic correction); there are bound states (E<0) that correspond classically to elliptic orbits, and scattering states (E>0) that correspond classically to hyperbolic orbits. The bound state eigenvalues are given by Balmer's formula
where n is a positive integer and is the ground state energy. For
hydrogen, 
eV.
- Schrödinger equation for a many-electron atom:
is the potential due to the nucleus:
and 
is the coulomb potential of interaction between the electrons:
where 
and so on. For the
time-independent equation, replace 
by 
.
The presence of makes the problem intractable analytically.
Numerical solutions are obtained by starting with the approximation that
each electron moves in the average potential of the others. In this way
accurate results can be obtained not only for atoms, but also for molecules
and chunks of matter.
References: Serway, chapter 29; PQRG, page 93; Fowler's notes for Phys 252, especially "Electron in a box" and the rest of the "Schrodinger equation" section.
Problem session 2
Assignment 1 solution: how to compute the gradient in cartesian and spherical coordinates. Using MAPLE: field plots using gradplot, integrals using int, range and properties of variables using assume and about. Given hints for problem set 2.
Lecture 5, Jan 29
Assigned problem set 3 (complex numbers, coupled pendulums, two-level quantum system)
Demos: two and three coupled pendulums, array of coupled torsion bars, standing waves and travelling waves.
Reviewed complex numbers and the quantum phase factor exp(-iwt). Demonstrated energy transfer and eigenmodes in coupled pendulums, as a model of two coupled quantum states. The wavefunction of the coupled quantum states is
and the time evolution is given by
Considered the case when 
(identical atoms, for instance). There are two
eigenstates: one with 
(bonding orbital,
energy E+V), and one with 
(antibonding orbital, energy E-V). For N atoms, get a band of N
eigenstates of the whole system from each atomic level (eigenstate of one
atom). Filling of bands. Metals (good conductors), semiconductors and
insulators.
References:
Question: In the equations for two coupled quantum states (such as atomic orbitals), what is V and does it have dimensions of energy?
Answer: In this case V denotes a number (not a function of x,y,z as it did in electrostatics) and represents an energy of interaction, suitably weighted over the atomic orbitals. For example, consider two hydrogen atoms that share one electron (hydrogen molecular ion). Then, in gaussian units,
where 
denotes the position of the electron, 
and 
those of the nuclei (just protons in this case); 
and 
are the
atomic eigenfunctions that were denoted as 
and 
for short.