Lecture 1: Basic Electrostatics
The force between two charges is given by Coulomb's law
where 
depends on the choice of units. In cgs electrostatic units, 
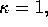F is in dynes, r in centimeters, 
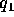and 
in
statcoulombs. In the MKS system, F is in newtons, r in meters,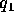 
and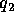 
in coulombs, and
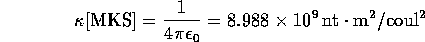
Thus two coulombs at the distance of one meter repel each other with the
very large force of 
or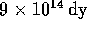 
(we will usually write 9 instead of 8.988... in the following).
Two coulombs at one cm repel each other with the force of
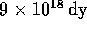. Hence
------------------------------------------------------------------
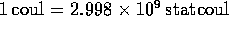
If charge q is at point x and charge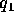 
is at
point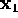 
, the Coulomb force is directed along the vector 
:
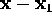This force can be regarded as the product of q times the
electric field E produced by 
at x. E
depends on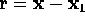 
and we can write
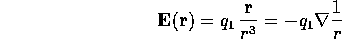
For an arbitrary distribution of charges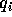 
, we have
and for a continuous charge distribution, 
:
=========================================
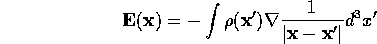
Insert on properties of 
-function as needed
=========================================
If the surface S encloses the charges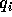 
where the normal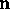 
is directed outwards. This is proved by noting
that for a single charge q (see Jackson's Fig. 1.2)
so that the flux of the electric field through the area element da is
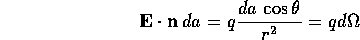
where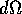 
is the solid angle subtended by da.
---------------------------------
For a continuous distribution
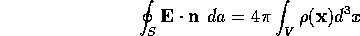
where V is the volume enclosed by S. Using the divergence theorem
we obtain the differential form of Gauss's law
---------------------------------
These are left by Jackson as Problems, and can be found in more elementary books. There are three basic types:
where q is the total charge inside the sphere. To the outside world, it is as if all the charge were in the center of the sphere. The analogous result for the gravitational field is due to Newton.
where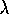 
is the total charge per unit length inside the cylinder of
radius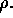 
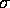by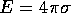 
.
The field of a unit point charge is 
. The
field of a set of charges can also be written as a gradient:
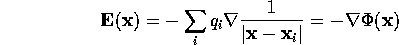
where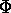 
is the electrostatic potential:
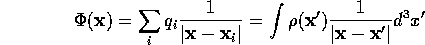
For any function 
, 
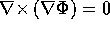. Hence
The physical meaning of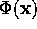 
is as follows: if there are no
charges at infinity, so that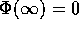 
, then 
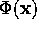is
the work required to bring a unit charge from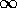 
to 
(the
other charges being fixed). More generally, the work required to bring a
charge q from point A to point B is
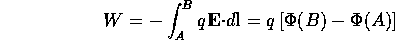
The work done depends only on the end points, not on the path; hence the net
work in going around a closed path is zero; the electric field is
conservative. These properties are just a consequence of 
as can also be seen from Stokes' theorem:
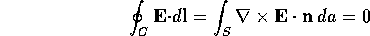
where S is any surface bounded by the closed contour C.
---------------------------
The esu unit of potential is the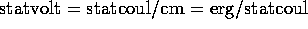 
.
The MKSA unit is the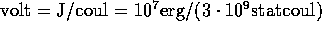 
. Thus
---------------------------
Starting from Coulomb's law we have derived the two differential field equations of electrostatics
The most general solution of the first equation can be written 
, where at this point 
is unspecified.
Inserting in the second equation, we find that 
must satisfy the
Poisson equation:
Conversely, one can show directly that the only solution of the Poisson equation that vanishes at infinity is the familiar
To prove that (1.3) is a solution of (1.2), we make use of
which is really nothing but Poisson's equation when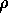 
is a point
charge. If this equation is granted, then
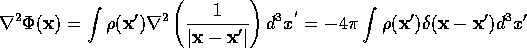
gives immediately 
.
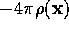Then, putting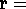 
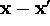, all we need to show is
that
The easiest way to proceed is to note that for 
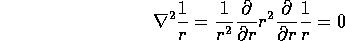
but for r=0 we have a singularity with integrated strength
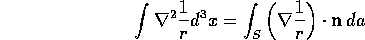
by the divergence theorem. The integral is conveniently evaluated on a
sphere of finite radius r, and it gives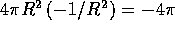 
.
Another way to handle the singular behavior is to replace 1/r with a ``regularized'' function, such as
and then let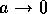 
. This is done in Jackson and may appeal to the
rigor-minded. ``Regularization'' procedures of this type are a way of life
in quantum electrodynamics, so Jackson takes the opportunity to show one
here.
------------------------------------
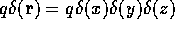
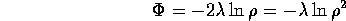
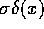
That is, the potential has a cusp and the field is discontinuous. For a
non-planar charge layer, there is the same discontinuity, but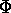 
is not
symmetric for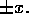 
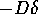
That is, the potential is discontinuous and the field vanishes, except
inside the dipole layer, where it cannot be seen. For a non-planar dipole
layer, there is the same discontinuity, but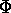 
is not antisymmetric for
A simple result applies for any dipole layer of constant D (see
Jackson's Fig. 1.7): 
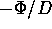is equal to the solid angle subtended by the
layer.
