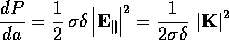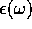 for
for 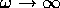 ? A full answer is needed for the following.
? A full answer is needed for the following.
1.
(a) What is the general behavior of 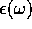 for
for 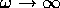 ? A full answer is needed for the following.
? A full answer is needed for the following.
(b) Show that the sum rule
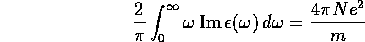
follows from the dispersion relation
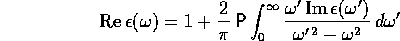
and from the behavior of 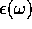 for
for 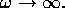 Supply the meaning of N and m.
Supply the meaning of N and m.
(c) The intensity of a plane wave propagating in the z direction
with frequency 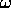 is observed to be proportional to
is observed to be proportional to 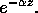 Relate the attenuation constant
Relate the attenuation constant  to the imaginary part of the index
of diffraction in the medium.
to the imaginary part of the index
of diffraction in the medium.
(d) What is the relation between 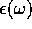 and the
complex index of diffraction
and the
complex index of diffraction 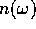 ? Can one write dispersion
relations for
? Can one write dispersion
relations for 
(e) By an argument similar to that in (b), or otherwise, evaluate
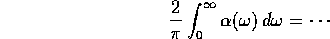
for a non-magnetic medium (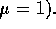
2.
Consider a cylindrical cavity (not necessarily a circular cylinder) with the axis in the z direction. Assume that the walls are perfectly conducting.
(a) What are the boundary conditions for the E and H fields on the side walls?
(b) What are the boundary conditions for E and H on the end walls?
(c) Describe qualitatively the lowest TM mode. You may use a cavity with a rectangular or circular cross section as an example.
(d) Describe qualitatively the lowest TE mode. You may use an example as above.
(e) Which mode has lowest frequency for a long, thin cavity? For a short cavity?
3.
(a) Write down the expression for the skin depth 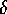 in a
medium of d.c. conductivity
in a
medium of d.c. conductivity 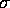 and
magnetic permeability
and
magnetic permeability 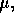 at
frequency
at
frequency 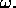 Describe conditions under which this expression is valid.
Describe conditions under which this expression is valid.
(b) Under the above conditions, how is the surface current K related to the E field at the surface? How is it related to the B field at the surface?
(c) What is the power dissipated per unit surface area?
SOLUTIONS
1.
(a) 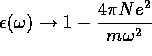 where N is the electron density, m the electron mass. This
formula also implies that
where N is the electron density, m the electron mass. This
formula also implies that 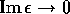 faster than
faster than 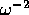 .
.
(b) Compare 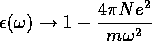 with
with 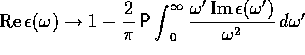 .
.
(c) 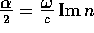
(d) 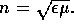 One can,
because
One can,
because  and
and 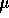 have no zeros for
have no zeros for 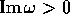 .
.
(e) Compare 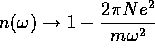 with
with
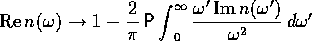 .
.
Get 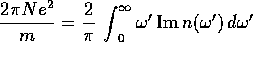 or
or
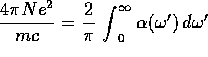
----------------------
2.
(a) and (b) If we introduce components parallel and
perpendicular to the wall, such as 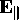 and
and 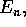 the
conditions on any wall are
the
conditions on any wall are 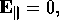
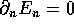 and
and 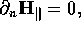
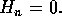 In particular on the
end walls
In particular on the
end walls 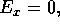
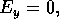
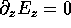 and
and 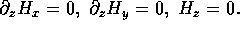
(c) In the lowest TM mode 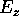 does not depend on z, hence the
frequency does not depend on the length of the cavity
does not depend on z, hence the
frequency does not depend on the length of the cavity 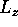 and is equal to
and is equal to  the lowest TM cutoff for a waveguide with the same cross section.
the lowest TM cutoff for a waveguide with the same cross section.
(d) In the lowest TE mode 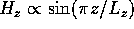 and the frequency
and the frequency 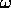 depends on
depends on 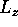 according to
according to
where 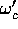 is the lowest TE cutoff for a waveguide with the
same cross section.
is the lowest TE cutoff for a waveguide with the
same cross section.
(e) Since 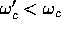 (see the Examples), the
lowest mode is TM for a short cavity, TE for a long cavity.
(see the Examples), the
lowest mode is TM for a short cavity, TE for a long cavity.
Example 1. For a box of sides 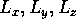 with
with 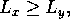 the lowest mode is TM
the lowest mode is TM for
for  (short cavity) and TE
(short cavity) and TE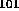 for
for  (long cavity). Explicitly, with
(long cavity). Explicitly, with 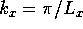 and
and 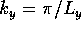 :
:
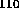 mode has fields
mode has fields

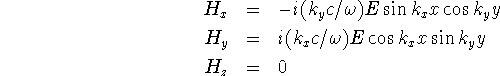
where 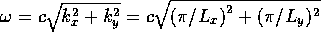 is the frequency. We see that
is the frequency. We see that 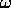 does not depend on
does not depend on  and is equal to the TM threshold
and is equal to the TM threshold 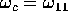 (in the usual notation).
(in the usual notation).
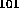 mode has fields
mode has fields
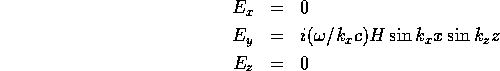
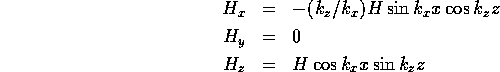
where 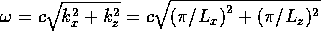 is the frequency. We see that
is the frequency. We see that 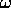 is of the form (1)
with
is of the form (1)
with ![]()
![]() (in the usual notation).
(in the usual notation).
Example 2. For a circular cylinder of radius R and
length  the lowest mode is TM
the lowest mode is TM for
for 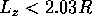 (short cavity)
and TE
(short cavity)
and TE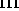 for
for 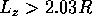 (long cavity). Explicitly, with
(long cavity). Explicitly, with 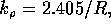
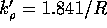 and
and 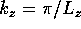 :
:
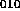 mode has fields
mode has fields


The frequency is 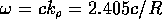 . We see that
. We see that 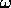 does not
depend on
does not
depend on 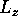 and is equal to the TM threshold
and is equal to the TM threshold 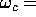
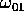 (in the usual notation).
(in the usual notation).
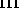 mode is doubly degenerate (
mode is doubly degenerate (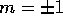 ). For comparison
with the fields in a box it is good to use the linear combination
). For comparison
with the fields in a box it is good to use the linear combination
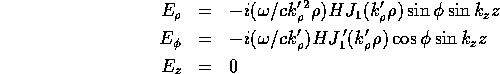
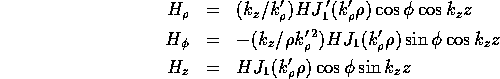
where 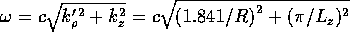 is the frequency. We see that
is the frequency. We see that 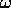 is
of the form (1) with
is
of the form (1) with 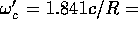
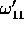 (in the usual notation).
(in the usual notation).
Comment: Jackson uses k for 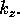 For the box he uses
For the box he uses 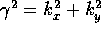 and for the circular cylinder he uses
and for the circular cylinder he uses 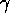 for
for 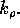
-------------------
3.
(a) 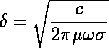 is valid
when
is valid
when  . One can always write
. One can always write 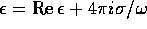 and the condition is
then
and the condition is
then 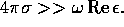 In many good conductors
In many good conductors  and
and 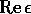 depend weakly on
depend weakly on 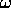 up to
frequencies in the infrared. The surface must also be nearly flat on the
scale of
up to
frequencies in the infrared. The surface must also be nearly flat on the
scale of 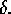
(b) 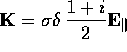 and
and 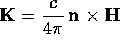
(c)