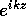 part and the
part and the 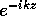 part,
work on each separately, and recombine them. This can be cumbersome.
part,
work on each separately, and recombine them. This can be cumbersome.
Jackson works out in detail the fields in a waveguide, then uses the
waveguide solutions to work out the fields in a cavity. His procedure is to
break up the cavity fields into the 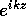 part and the
part and the 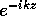 part,
work on each separately, and recombine them. This can be cumbersome.
part,
work on each separately, and recombine them. This can be cumbersome.
One can obtain formulas that work directly for fields proportional to any combination of sinusoidal or exponential functions. The result shown here is in cartesian coordinates, and thus it is especially suited for box-shaped cavities.
Start from Maxwell's equations written out explicitly:
Assuming only that the each field component satisfies 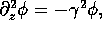 we can obtain all the other field components from the
``superpotentials''
we can obtain all the other field components from the
``superpotentials'' 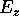 and
and 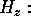
To derive (7), for example, all we need is Eq. (1) and the z derivative of (5):
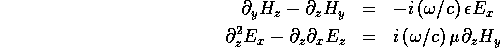
Eliminate  from these two equations and replace
from these two equations and replace 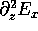 with
with 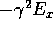 .
.
Jackson is rather vague on this point. For a cavity with perfectly
conducting walls and end walls perpendicular to the z axis:
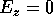 on the side walls and
on the side walls and  on the end walls
on the end walls
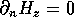 on the side walls and
on the side walls and 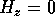 on the end walls
on the end walls
To derive these boundary conditions, we note first that  must be inversely proportional to the conductivity, otherwise the current
would be infinite. This implies that on the side walls
must be inversely proportional to the conductivity, otherwise the current
would be infinite. This implies that on the side walls  and on the
end walls
and on the
end walls 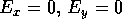 and their lateral derivatives also vanish. Then we
can use
and their lateral derivatives also vanish. Then we
can use  and
and 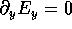 in the divergence equation
in the divergence equation
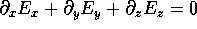 to conclude that
to conclude that 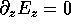 on the end walls
on the end walls We can also use
We can also use 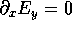 and
and 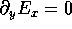 in the equation
in the equation 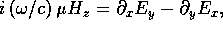 from
from 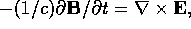 to conclude that
to conclude that 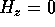 on the end walls. In general
the normal component
on the end walls. In general
the normal component  vanishes on a wall, and so do its lateral
derivatives.
vanishes on a wall, and so do its lateral
derivatives.
Finally, we show that the normal derivative  vanishes on the
side walls. Consider a wall element and orient the x axis normal to it.
Use
vanishes on the
side walls. Consider a wall element and orient the x axis normal to it.
Use  from
from 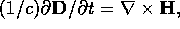 and
note that
and
note that 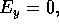 because it is a parallel component of
because it is a parallel component of  and
that
and
that 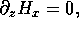 because it is a lateral derivative of the normal
component of
because it is a lateral derivative of the normal
component of 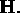 It follows that
It follows that 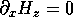 . In general,
. In general, 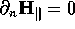 on a wall.
on a wall.