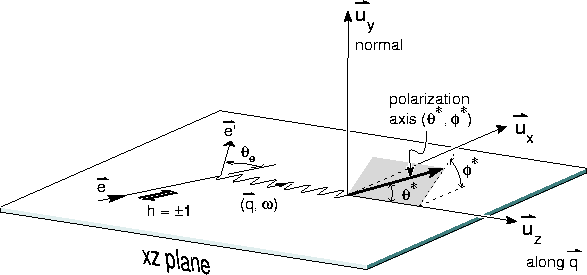
Figure 2: Coordinate system for 
with orientation of polarization axis
shown.
Following Donnelly and Raskin[3, 4]
we can express the inclusive e-N cross section as a sum of an unpolarized part
( 
), that corresponds to the elastic cross section
, and a polarized part ( 
),
that is different from zero
only when the beam is longitudinally polarized (helicity h):
The asymmetry is then
As stated above, is just the elastic unpolarized free e-N cross
section, and specifically for neutrons it reads
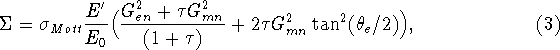
where 
is the electron's initial (final) energy, 
, 
is the neutron mass, 
is the square of the four- momentum
transfer and 
are the neutron Coulomb and magnetic form factors. The polarized
part contains two terms, associated with the possible directions of the target
polarization. The full expression is given below, with the kinematic factors and the
nucleon form factors both evaluated in the laboratory frame (the elastic recoil factor
reduces to
in the extreme relativistic limit):
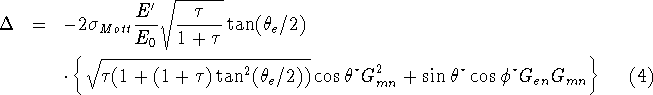
where 
and 
are the laboratory angles of the
target polarization vector with 
along the 
direction and
normal to the electron scattering plane. It is clear that to extract 
the target has to be polarized longitudinally (i.e.
) and perpendicular to ( 
). For this special
condition, the asymmetry simplifies to
This result was also obtained by Arnold et al.[5] who considered the measurement of the polarization of the recoil neutron, instead of using a polarized target.
The foregoing analysis is valid for free nucleons, and it has been reinterpreted in the
case of neutrons in polarized nuclei. For the specific case of polarized deuterium
nuclei, the exclusive process involving the detection of the neutron after the
electrodisintegration can be similarly
described[3] in an expression where
the interference between and 
is contained in the polarized part.
The neutron asymmetry is related to the deuteron asymmetry
, as 
where 
is a correction factor (0.92) for the
D-state of the deuteron.
There are different ways to exploit polarization observables
for a determination of
.
One can either use a polarized beam and target as discussed above, or one can use a
polarized beam and measure the polarization of the recoiling nucleon. In practice, the
measurement using a polarized beam and target involves determining the experimental
asymmetry
which depends on the normalized numbers of counts for two opposite
helicities,
and 
. The same expression occurs in the recoil polarimetry method, with the
obvious reinterpretation of 
as the analyzing power of the polarimeter, 
;
is then the polarization 
of the recoiling nucleon, and 
are
the numbers of counts in the up(down) segments of the polarimeter.
Our studies of these alternatives have led us to choose the polarized target technique.
We have found that it allows us to measure 
over a larger range of 
than the
alternative, and it avoids the difficult problem of a new calibration of the recoil
polarimeter for every neutron energy (for every ). In addition, the same setup
(target and detectors)
can be used to check the experimental technique and
the reaction mechanism, assumed to be quasi-free knockout , by measuring 
which
is known over the range we wish to study.
There are two different polarized targets which provide in effect polarized neutrons,
polarized deuteron and polarized 
He. We have chosen polarized deuteron, as the
theoretical description of the
(e, e'n) process is on a much firmer footing. For the 2N-system the final state
interaction can be treated exactly, while this is questionable for
A = 3. The role of the D-state in the ground state wave function
and the contributions of MEC, are under better control. Accurate calculations are already
available, while for A = 3 we are still speculating on the size of the effects. At the same
time, a deuteron target allows the experimental check on procedures and reaction mechanism
through the comparison of the
d(e,e'n) and d(e,e'p) reactions. Arenhövel et al.[5] have shown that, for
the case of the deuteron, the uncertainties introduced by the deuteron structure are very
small if one concentrates on the strength corresponding to quasielastic e-n scattering
with neutrons of small initial momentum. For such kinematic conditions
and for the special case of the two-nucleon
system, FSI can be accurately computed,
and does not contribute significantly to the systematic errors. The effects of MEC, which
for A = 2, also can be calculated with reasonable confidence, are small as well. Effects of
both FSI and MEC are much smaller than the statistical and systematical errors of the
experiment we propose.
To determine the region of where the proposed technique may be most effective, the
evaluation of a figure of merit (FOM) has become customary. In the present case, the
figure of merit is related to the time required to accumulate the number of counts needed
to determine the asymmetry to
a given precision. This number is proportional to the
product of the square of the asymmetry times the cross section (averaged over the
acceptances of our detectors), so the FOM is defined as
Obviously, this quantity depends on the choice
of a model for .
Several models have been tried to describe the existing data, which extend
from the photon point to 
.
Among those deserving special attention are the so-called ``dipole'' model
which uses the form 
, with 
, in fact setting the Dirac form factor 
to zero, in the full
expression for the Sachs form factor 
;
the phenomenological parameterization of Galster et al.[7],
; and the models that seek a connection between the value
of of the form factors at low momentum transfer and the asymptotic values of the Dirac
and Pauli form factors and 
predicted by perturbative
QCD, in particular the one proposed by Gari and Krümpelmann[8].
In Figure 3 we present the dependence of in those three instances. It can
be seen that the dipole model is higher than the two others, and in fact it is an upper
bound to the experimental data. On the other hand, the Galster parameterization (with the
Feshbach-Lomon potential) gives a good fit for p = 5.6. We used these two models, which
cover a broad range of possible values for the
dependence of , to compute the FOM's. These studies show that the
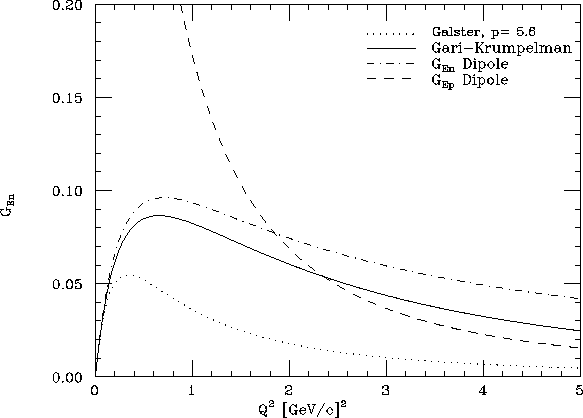
Figure 3: dependence of for three different models.
scattered electron angle 
has to be as forward as possible, even
though the change of FOM with angle is not large.
For increasing momentum transfer, the FOM drops by a factor of
(depending on the model)
from its maximum value to the largest momentum transfer considered here,
. This places a practical limit on the upper value of the
attainable momentum transfer, independent of other technical complications that arise
from the high kinetic energy of the recoil neutrons, and the opening of inelastic
and 
channels. Therefore, in the present experiment, we will attempt
to extract at four values of , starting at about 0.5 (GeV/c) 
, up to 2
(GeV/c) .
To obtain these values of the four-momentum transfer, a combination of beam energies and scattering angles are chosen such as to maximize the FOM, within the laboratory capabilities and facilities. The kinematical settings we have chosen are displayed if table 1.
which is the electron energy loss at the quasielastic peak, including
the average separation energy of the nucleon; 
which is the direction of the
target magnetic field relative to the beam in the laboratory reference frame (main
coordinate system), and is perpendicular to , corresponding to the values
; and 
is the kinetic energy of the recoil
neutrons in parallel kinematics (i.e. zero initial momentum).
The theoretical studies performed indicate clearly that
will provide a clean determination of
with small systematic errors. This is an important criterion given the fact that past
attempts to measure were all limited by systematic errors in both experiment and,
even more so, in the theoretical input necessary to infer .
