Heavy Damping: Pendulum in Molasses
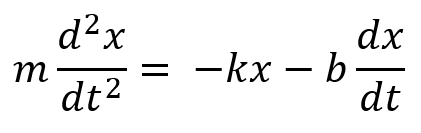
This applet is a first look at the behavior of a heavily damped oscillator, described by the differential equation above. The full mathematical details can be found in my lecture. We’ve set initial value of the damping constant b = 5. The mass m, the spring constant k, and the initial position and velocity can be changed using the sliders to the right.
Heavy damping makes it so that there are two different time scales in the motion, as you will discover on trying the walk-through below.
Walk-Through
As a warm up, let's look at damped motion without a spring.
Set k1 = 0, m1 = 2, v1 = 1.2, b = 5.
The mass comes slowly to rest. Approximately how long did that take?
How do you predict this will change if you halve the damping? Check it out!
What about if you double the initial speed? What if you halve the mass? Think about these before you try it--check your intuition!
Can you guess what the formula looks like for distance traveled? Apart from a constant, the formula can be found just using dimensions. Try it. What about a characteristic time?
Now bring in the spring: to see how the spring changes the motion, you can toggle on a second oscillator, and compare the paths with and without the spring.
Leave k1 = 0, but put k2 = 0.3, v1 = v2 = 1.2. Everything else the same. First predict how this will affect the terms, then press play. Describe the difference the spring makes. This brings in another time constant: time of decay. Find how long it takes to drop to half its maximum displacement. Find how this changes on varying the mass, the spring constant, and the damping.
Here's the relevant lecture.
Program by: Carter Hedinger