To determine the circulation about the airfoil we need an additional
condition on the flow field. If we think of the total flow as being composed
of a uniform contribution (with no circulation) plus a circulatory
contribution, then the circulation 
will adjust itself until the
total flow leaving the trailing edge of the airfoil is smooth. This is
called the Kutta-Joukowsky condition , and uniquely determines the circulation, and therefore the lift,
on the airfoil. The origin of this condition can be seen from Fig. 4.3.
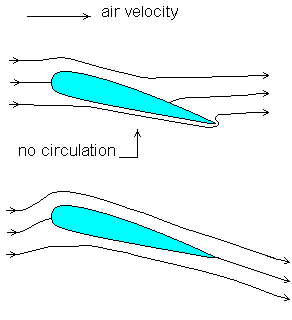
Figure 4.3: The development of circulation about an airfoil.
We initially have flow without circulation, with two stagnation points on the upper and lower surfaces of the airfoil. The fluid on the lower surface of the airfoil must accelerate around the sharp trailing edge in order to reach the rear stagnation point on the upper surface. This actually requires that the fluid velocity at the trailing edge be infinite--an unlikely circumstance in a viscous fluid. This flow configuration is unstable, and the rear stagnation point gets washed downstream, until it coincides with the trailing edge of the airfoil. At this point there is a net circulation about the airfoil, with the zero velocity stagnation point ``cancelling'' the infinite velocity at the trailing edge, resulting in smooth flow from the trailing edge. Now in a nonviscous fluid circulation is conserved--this is known as the Kelvin circulation theorem . Since at high Reynolds numbers the viscosity is only really important in the boundary layer (again assuming that it remains attached), then the circulation should be approximately conserved for flow of a viscous fluid about an airfoil at high Re. To compensate for the circulation which is established about the airfoil, a starting vortex with the opposite circulation is produced downstream of the airfoil. This is demonstrated in a dramatic way in the classic flow visualizations of Prandtl--see the accompanying figures.
This starting vortex (often called the downwash )
places limitations the spacing of take-offs. The downwash usually becomes
turbulent, and for a large jet the downwash can actually flip small planes.
How long does it take before the vortex decays away due to viscosity?
Dimensional analysis tells us that 
, with L the typical
size of the vortex. If we take L=20 cm, and 
m 
s 
, then 
s. This is an overestimate, but it does indicate
that vortices in air can be long-lived entities. The typical spacing between
jets is about 90 s, apparently enough time for the vorticity to decay away
to a manageable level.
With these considerations it is possible to calculate the lift on an airfoil
in terms of its geometry and angle of attack. The circulation about a
symmetric airfoil at an angle of attack 
and chord c is
approximately 
, so that the lifting force
per unit length is 
. This information is
often expressed in terms of the coefficient of lift (per unit length) for
the airfoil, defined as
For more complicated airfoils the lift coefficient must be computed using numerical methods; typical plots of coefficient of lift as a function of angle of attack are shown in Fig. 4.4. It is seen that, for small angles of attack, Eq. (4.2) works very well, and even better is the simple linear approximation cL = 2pa with a in radians, or cL = 0.11a with a in degrees (as in the figure).
Figure 4.4: Lift coefficient versus angle of attack
for the symmetric airfoil NACA 0009 and the cambered airfoil NACA 2408.
A cambered airfoil can generate lift at zero angle of attack; cambered airfoils are the norm on modern airplanes. Notice that once the angle of attack exceeds a critical value the flow separates from the top surface of the airfoil, resulting in a precipitous reduction in lift and an increase in the drag (due to pressure drag); this is called the stall angle, and beyond this angle the airfoil is said to be stalled.
