From a Circling Complex Number to the Simple Harmonic Oscillator

Michael Fowler

Describing Real Circling Motion in a Complex Way

We’ve seen that any complex number can be written in the form $z = r e^{i θ}$ , where $r$ is the distance from the origin, and $θ$ is the angle between a line from the origin to $z$ and the $x$ -axis. This means that if we have a set of numbers all with the same $r,$ but different $θ$ ’s, such as $r e^{i α}, r e^{i β}$ , etc., these are just different points on the circle with radius $r$ centered at the origin in the complex plane.

Now think about a complex number that moves as time goes on: $z (t) = A e^{i ω t} .$

At time $t, z (t)$ is at a point on the circle of radius $A$ at angle $ω t$ to the $x$ -axis. That is, $z (t)$ is going around the circle at a steady angular velocity $ω$ . We can also write this:

$z (t) = A e^{i ω t} = A \cos ω t + i A \sin ω t$

and see that the point $z = x + i y$ is at coordinates $(x, y) = (A \cos ω t, A \sin ω t) .$

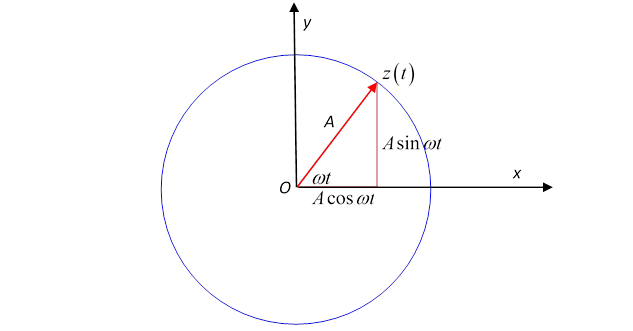
The angular velocity is $ω$ , the actual velocity in the complex plane is $d z (t) / d t .$

Let’s differentiate with respect to time:

$\frac{d}{d t} A e^{i ω t} = \frac{d}{d t} A (\cos ω t + i \sin ω t) = i ω A e^{i ω t} = i ω A (\cos ω t + i \sin ω t) = i ω A \cos ω t - ω A \sin ω t .$

Exercise: what are the $x$ and $y$ components of this velocity regarded as a vector? Show that it is perpendicular to the position vector. Why is that?

This differential equation has real and imaginary parts on both sides, so the real part on one side must be equal to the real part on the other side, and the same for imaginary parts. That gives

$\frac{d}{d t} \cos ω t = - ω \sin ω t, \frac{d}{d t} \sin ω t = ω \cos ω t$

so differentiating the exponential is consistent with the standard results for trig functions.

Differentiating one more time,

$\frac{d^{2}}{d t^{2}} A e^{i ω t} = - ω^{2} A e^{i ω t} .$

Again going to the picture of a complex numbers as a two-dimensional vector, this is just the acceleration of an object going round in a circle of radius $A$ at angular velocity $ω,$ and is just $A ω^{2}$ towards the center of the circle, the familiar $r ω^{2} = v^{2} / r .$ Thinking physics here, this is the motion of an object subject to a steady central force.

Follow the Shadow: Simple Harmonic Motion

But what if we just equate the real parts of both sides? That must be a perfectly good equation: it is

$\frac{d^{2}}{d t^{2}} A \cos ω t = - ω^{2} A \cos ω t$

This is just the $x$ -component of the circling motion, that is, it is the “shadow” of the circling point on the $x$ -axis.

Animation here!

Forgetting for the moment about the circling point, and staring at just this $x$ -axis equation, we see it describes the motion of a point always having acceleration towards the origin (that is, the minus sign ensures the acceleration is in the opposite direction to that of the point itself from the origin) and the magnitude of the acceleration is proportional to the distance of the point from the origin.

In fact, motion of this kind is very common in nature! It is called simple harmonic motion.

Mass Hanging on Spring

A simple standard example is a mass hanging on a spring. If it is initially at rest, and the spring has length $L$ (stretched from its natural length to balance $m g$ ) then if it is displaced a distance $x$ from that equilibrium position, from Hooke's Law the spring will exert an extra force $- k x$ and the equation of motion will be

$m \frac{d^{2} x}{d t^{2}} = - k x .$

This is exactly the equation of motion satisfied by the “shadow” on the $x$ -axis of the point circling at a steady rate.

The general solution is $x (t) = A \cos (ω t + δ)$ , where a possible phase $δ$ is included so that the point can be anywhere in its oscillation at $t = 0.$

previous index next