A New Thermodynamic Variable: Entropy

Michael Fowler

Introduction

The word “entropy” is sometimes used in everyday life as a synonym for chaos, for example: the entropy in my room increases as the semester goes on. But it’s also been used to describe the approach to an imagined final state of the universe when everything reaches the same temperature: the entropy is supposed to increase to a maximum, then nothing will ever happen again. This was called the Heat Death of the Universe, and may still be what’s believed, except that now everything will also be flying further and further apart.

So what, exactly, is entropy, where did this word come from? In fact, it was coined by Rudolph Clausius in 1865, a few years after he stated the laws of thermodynamics introduced in the last lecture. His aim was to express both laws in a quantitative fashion.

Of course, the first law $—$ the conservation of total energy including heat energy $—$ is easy to express quantitatively: one only needs to find the equivalence factor between heat units and energy units, calories to joules, since all the other types of energy (kinetic, potential, electrical, etc.) are already in joules, add it all up to get the total and that will remain constant. (When Clausius did this work, the unit wasn’t called a Joule, and the different types of energy had other names, but those are merely notational developments.)

The second law, that heat only flows from a warmer body to a colder one, does have quantitative consequences: the efficiency of any reversible engine has to equal that of the Carnot cycle, and any nonreversible engine has less efficiency. But how is the “amount of irreversibility” to be measured? Does it correspond to some thermodynamic parameter? The answer turns out to be yes: there is a parameter Clausius labeled entropy that doesn’t change in a reversible process, but always increases in an irreversible one.

Heat Changes along Different Paths from a to c are Different!

To get a clue about what stays the same in a reversible cycle, let’s review the Carnot cycle once more. We know, of course, one thing that doesn’t change: the internal energy of the gas is the same at the end of the cycle as it was at the beginning, but that’s just the first law. Carnot himself thought that something else besides total energy was conserved: the heat, or caloric fluid, as he called it. But we know better: in a Carnot cycle, the heat leaving the gas on the return cycle is less than that entering earlier, by just the amount of work performed. In other words, the total amount of “heat” in the gas is not conserved, so talking about how much heat there is in the gas is meaningless.

To make this explicit, instead of cycling, let’s track the gas from one point in the $(P, V)$ plane to another, and begin by connecting the two points with the first half of a Carnot cycle, from $a$ to $c :$

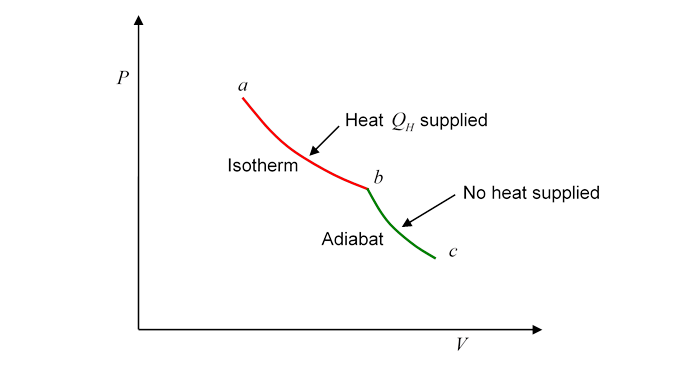
Evidently, heat $Q_{H}$ has been supplied to the gas $—$ but this does not mean that we can say the gas at $(P_{c}, V_{c})$ has $Q_{H}$ more heat than the gas at $(P_{a}, V_{a}) .$ Why not? Because we could equally well have gone from $a$ to $c$ by a route which is the second half of the Carnot cycle traveled backwards:

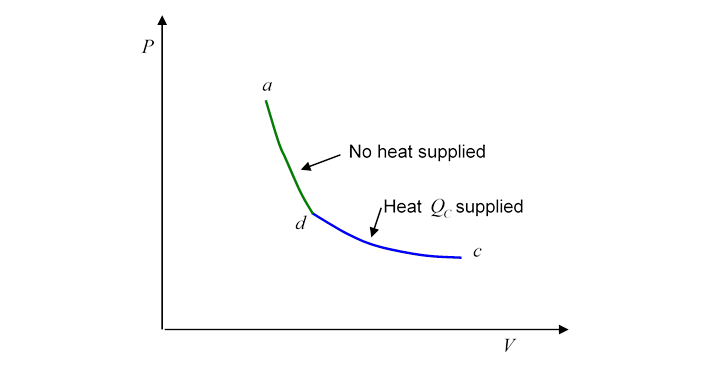
This is a perfectly well defined reversible route, ending at the same place, but with quite a different amount of heat supplied!

So we cannot say that a gas at a given $(P, V)$ contains a definite amount of heat. It does of course have a definite internal energy, but that energy can be increased by adding a mix of external work and supplied heat, and the two different routes from $a$ to $c$ have the same total energy supplied to the gas, but with more heat and less work along the top route.

But Something Heat Related is the Same: Introducing Entropy

However, notice that one thing (besides total internal energy) is the same over the two routes in the diagrams above:

the ratio of the heat supplied to the temperature at which is was delivered:

$Q_{H} / T_{H} = Q_{C} / T_{C} .$

(This equation was derived in the last lecture.)

Of course, we’ve chosen two particular reversible routes from $a$ to $c :$ each is one stretch of isotherm and one of adiabat. What about more complicated routes?

Let’s begin by cutting a corner in the previous route:

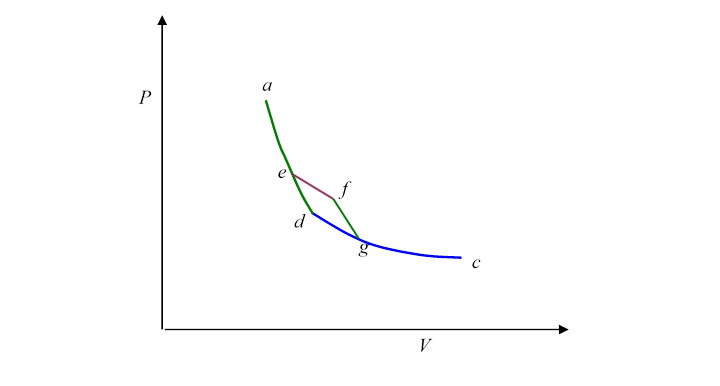
Suppose we follow the path $a e f g c$ instead of $a d c,$ where $e f$ is an isotherm and $f g$ an adiabat. Notice that $e f g d$ is a little Carnot cycle. Evidently, then,

$\frac{Q_{e f}}{T_{e f}} = \frac{Q_{d g}}{T_{C}},$

and

$Q_{C} = Q_{d g} + Q_{g c},$

from which

$\frac{Q_{H}}{T_{H}} = \frac{Q_{e f}}{T_{e f}} + \frac{Q_{g c}}{T_{C}},$

But we can now cut corners on the corners: any zigzag route from $a$ to $c,$ with the zigs isotherms and the zags adiabats, in other words, any reversible route, can be constructed by adding little Carnot cycles to the original route. In fact, any path you can draw in the plane from a to c can be approximated arbitrarily well by a reversible route made up of little bits of isotherms and adiabats.

We can just apply our “cutting a corner” argument again and again, to find

$\sum_{a}^{c} \frac{Q_{i}}{T_{i}} = \int_{a}^{c} d Q / T is the s a m e for all reversible paths$

where the $i$ labels intermediate isothermal changes.

We can therefore define a new state variable, $S,$ called the entropy, such that the difference

$S (P_{2}, V_{2}) = S (P_{1}, V_{1}) + \int_{(P_{1}, V_{1})}^{(P_{2}, V_{2})} \frac{d Q}{T}$

where the integral is understood to be along any reversible path $—$ they all give the same result. So knowing $S (P_{1}, V_{1})$ at a single point in the plane, we can find its value everywhere, that is, for any equilibrium state.

This means an ideal gas has four state variables, or thermodynamic parameters: $P, V, T, S .$ Any two of them define the state (for a given mass of gas), but all four have useful roles in describing gas behavior. If the gas is not ideal, things get a lot more complicated: it might have different phases (solid, liquid, gas) and mixtures of gases could undergo chemical reactions. Classical thermodynamics proved an invaluable tool for analyzing these more complicated systems: new state variables were introduced corresponding to concentrations of different reactants, etc. The methods were so successful that by around 1900 some eminent scientists believed thermodynamics to be the basic science, atomic theories were irrelevant.

Finding the Entropy Difference for an Ideal Gas

In fact, for the ideal gas, we can find the entropy difference between two states exactly! Recall that the internal energy of a monatomic gas, the total kinetic energy of the molecules, is $\frac{3}{2} n R T$ for $n$ moles at temperature $T .$ For a diatomic gas like oxygen, the molecules also have rotational energy because they’re spinning, and the total internal energy is then $\frac{5}{2} n R T$ (this is well-confirmed experimentally). The standard way to write this is

$total internal energy = C_{V} T$

because if the gas is held at constant volume, all ingoing heat becomes internal energy. Note that $C_{V}$ here is for the amount of gas in question, it is not specific heat per mole.

Suppose now we add heat $d Q,$ but allow volume variation $d V$ at the same time. Then, for $n$ moles of gas,

$\begin{matrix} d Q = C_{V} d T + P d V \\ = C_{V} d T + n R T \frac{d V}{V} \end{matrix}$

$\int_{(P_{1}, V_{1})}^{(P_{2}, V_{2})} \frac{d Q}{T} = C_{V} \int_{(P_{1}, V_{1})}^{(P_{2}, V_{2})} \frac{d T}{T} + n R \int_{(P_{1}, V_{1})}^{(P_{2}, V_{2})} \frac{d V}{V}$

So the entropy change depends only on the final $T$ and $V,$ in other words, the final $P$ and $V$ since we always have $P V = n R T .$ This is just restating what we’ve already established:

$S$ is a state variable,

the (macroscopic) state of the ideal gas is fully determined by $P, V$ (or $P, T$ ), and therefore so is the entropy $S .$

This means we can get to the final state any way we want, the entropy change is the same, we don’t have to go by a reversible route!

Entropy in Irreversible Change: Heat Flow Without Work

Irreversible processes are easy to find $—$ just hold something hot. When heat $Q$ flows from a body at $T_{H}$ to one at $T_{C},$ simply by thermal contact, by definition the entropy change is:

$Δ S = \frac{Δ Q}{T_{C}} - \frac{Δ Q}{T_{H}} > 0$

since the temperatures must be different for heat to flow at all. There is no energy loss in this heat exchange, but there is a loss of useful energy: we could have inserted a small heat engine between the two bodies, and extracted mechanical work from the heat flow, but once it’s flowed, that opportunity is gone. This is often called a decrease in availability of the energy. To get work out of that energy now, we would have to have it flow to an even colder body by way of a heat engine.

Note that the increase in entropy is for the two bodies considered as a single system. The hot body does of course lose entropy. Similarly, when a heat engine has less than Carnot efficiency, because some heat is leaking to the environment, there is an overall increase in entropy of the engine plus the environment. When a reversible engine goes through a complete cycle, its change in entropy is zero, as we’ve discussed, and the change in entropy of its environment, that is, the two reservoirs (hot and cold) taken together is also zero: entropy is simply transferred from one to the other.

The bottom line is that entropy change is a measure of reversibility:

· for a reversible process, total entropy change (system + environment) ΔS = 0,

· for an irreversible process, total entropy increases, ΔS > 0.

Entropy Change without Heat Flow: Opening a Divided Box

Now consider the following scenario: we have a box of volume $2 V,$ which is two cubes of volume $V$ having a face in common, and that face is a thin partition in the box.

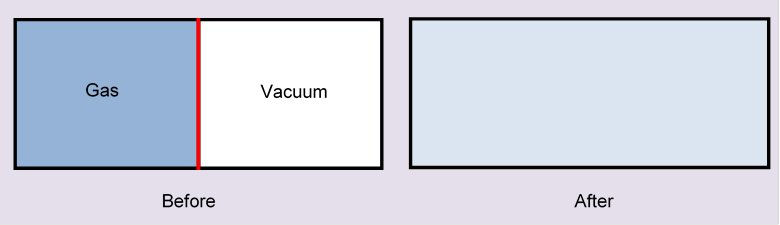
At the beginning, $n$ moles of ideal gas are in the left-hand half of the box, a vacuum in the other half. Now, suddenly, the partition is removed. What happens? The molecules will fly into the vacuum, and in short order fill the whole box. Obviously, they’ll never go back: this is irreversible.

To see how quickly the gas fills the other half, and how very different it is if there is already some (different) gas there, explore with the diffusion applet. For the current case, set the number of green molecules to zero.

Question: What happens to the temperature of the gas during this expansion?

Answer: Nothing! There’s no mechanism for the molecules to lose speed as they fly into the new space. (Note: we don’t need a molecular model to see this $—$ an ideal gas expanding against nothing does no work.)

Question: What happens to the pressure? Can you explain this?

Question: What is the entropy change? It is $n R \ln 2.$

But no heat flowed in on this route!

If we had followed a reversible route, for example moving slowly along an isothermal, letting the partition gradually retreat to one end of the box like a piston in a cylinder, we would have had to supply heat. Fig 6

That supplied energy would have all been used in pushing the cylinder, the gas itself ending up in the same state as just removing the partition. But we would have had a nonzero $\int d Q / T .$

Just removing the partition quickly there is no heat transfer, and this action doesn’t correspond to any path in the P, V plane, since each point in that plane represents a gas in equilibrium at that $P, V .$ Nevertheless, the initial and final states are well defined (after the partition-removed state has reached equilibrium, which will happen very quickly) and they’re the same as the initial and final states in the isothermal expansion. So, even though there’s no heat transfer during the expansion into a vacuum, there is an increase in entropy, and this increase is the same as in the isothermal expansion.

Clausius realized that the entropy measured both something to do with heat content, but also how “spread out” a system was. This is clear for the ideal gas: the entropy change formula has two terms, one depending on the temperature difference, the other the volume difference. We shall return to this in the next lecture, when we examine entropy in the kinetic theory.

The Third Law of Thermodynamics

Notice the argument above only tells us entropy difference between two points, it’s a bit like potential energy. Actually, though, there is a natural base point: a system at absolute zero temperature has zero entropy. This is sometimes called the Third Law of Thermodynamics, or Nernst’s Postulate, and can only be really understood with quantum mechanics. We don’t need it much for what we’re doing here, we only work with entropy differences, but it makes things convenient because we can now write $S (P, V)$ without ambiguity.

previous index next