The Laws of Thermodynamics and Limits on Engine Efficiency

Michael Fowler

The Laws of Thermodynamics

(Picture below from St. Andrews)

In 1850, Rudolph Clausius, a German physicist, created the science of thermodynamics. He was convinced by Joule’s experiments (he didn’t know about Mayer’s work at the time) that total energy, including kinetic, potential, electrical, and, importantly, heat, was conserved, he called this:

The first law of thermodynamics: total energy, including heat energy, is always conserved.

He explicitly assumed that heat was just the kinetic energy of the moving particles that made up a body. He was the first to make clear that Carnot’s analysis of the heat engine (the cycle) was almost right except that the “caloric fluid”, meaning heat, wasn’t actually conserved—less of it was dumped in the cold reservoir than was taken from the hot one. The difference of course was the work done (in an ideal engine). Engines at the time were so inefficient that this loss of heat energy wasn’t obvious.

But abolishing the caloric fluid in favor of overall energy conservation raised another problem. The fluid theory had been highly successful in describing heat flow through solid materials, like electric current flow but with temperature gradients replacing voltage drops, different materials having different thermal conductivities, etc.

(Note: Fourier revolutionized mathematics by inventing Fourier series, his method of analyzing caloric fluid flow. In fact Kelvin used it in 1862 to estimate the rate of cooling of the earth. Kelvin’s conclusion that the earth was twenty million years old or so (much older would be much colder) led to decades of debate with Darwinians and geologists, both of whom needed much more time, for evolution and rock strata formation respectively. The debate went on until the 1890’s when the discovery of radioactivity made clear that this unsuspected source of subterranean heat was keeping us all warm. Once this extra heat was included, the heat flow analysis gave a much older earth—and everyone was in agreement.)

In the caloric theory, then, heat flowed naturally from a high temperature to a low temperature, just as a fluid flows downhill, or an electric current to a lower voltage. And, of course, this heat flow is invariably observed in nature. But the first law makes no such prediction: the conservation of total energy would be equally satisfied if heat flowed from a cold body to a hot body.

Conclusion: since the caloric theory is dead, we need to add this universally observed direction of heat flow as another law. Here it is:

The Second Law of thermodynamics: heat always flows from a warm body to a cooler one, never the other way. An equivalent statement is that we cannot devise an engine, working in a cycle, that causes heat to flow from cold to warm unless we supply outside energy.

Translation: your refrigerator won’t work if it’s not plugged into some power supply, and no-one will ever design one that does.

Unlike the first law, there are many ways of writing this Second Law: our wording above is a paraphrase of Clausius’ original formulation. Kelvin gave it a more “engineering” look:

It is impossible to devise an engine which, working in a cycle, shall produce no effect other than the extraction of heat from a reservoir and the performance of an equal amount of mechanical work.

Exercise: think about how you might prove these two definitions amount to the same thing.

The Second Law can also be stated in terms of entropy, a concept we’ll cover in the next lecture.

It’s important to note that the first law of thermodynamics, the conservation of total energy including heat, would not be violated by an engine that powered a ship by extracting heat energy from the surrounding seawater. This Second Law is saying something new: you can’t do that! And, this Second Law does not follow from the first by logical deduction $—$ it comes (like the first) from experiment and observation.

How the Second Law Limits Engine Efficiency

An important consequence of the Second Law is that no engine can be more efficient than the Carnot cycle. Essentially, this is because a “super-efficient” engine, if one existed, could be used to drive a Carnot cycle in reverse, which would pump back to the hot reservoir the heat the super-efficient engine dumped in the cold reservoir, and the net effect of the two coupled engines would be to take heat from the hot reservoir and do work, contradicting the Second Law.

To see this, we plot the heat/energy flow for the Carnot cycle:

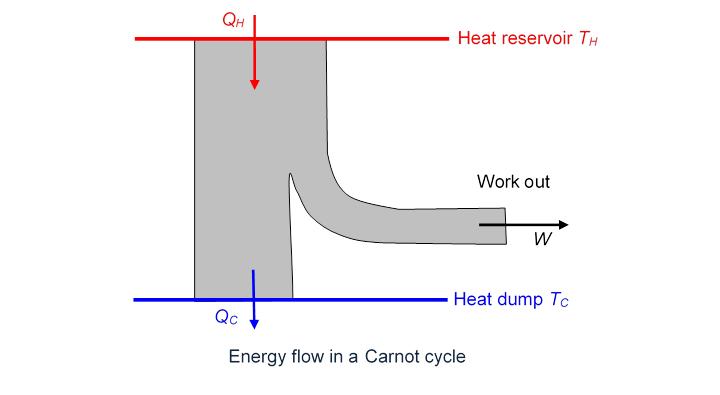
Here $Q_{H} = Q_{C} + W$ (all expressed in Joules, of course).

Since the engine is reversible, it can also be run backwards (this would be a refrigerator): outside work is supplied, and heat is extracted from a cold reservoir and dumped into a hot reservoir:

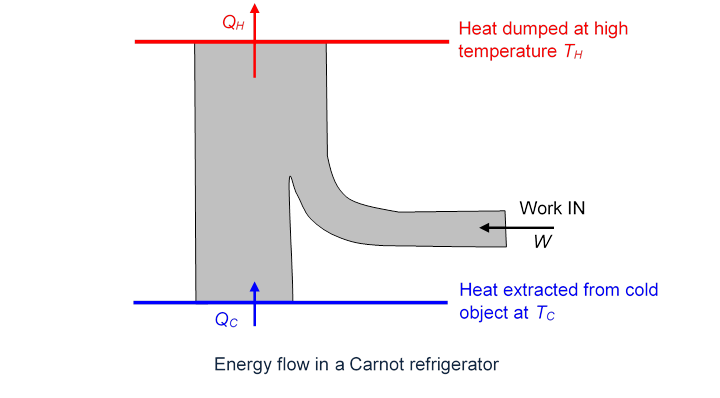
Suppose now we have a super-efficient engine, represented by the first diagram above, and dumping the same heat per cycle $Q_{C}$ into the cold reservoir, but taking in more heat energy $Q_{H} + Δ$ Joules from the hot reservoir, and performing more work: $W + Δ .$

Now, we hook up our super-efficient engine to the “Carnot refrigerator” in the other diagram above. The refrigerator sucks out of the cold reservoir all the heat the super-efficient engine dumped there, and needs $W$ Joules of work per cycle to do it. The super-efficient engine can provide this, and there are still $Δ$ Joules of work to spare. Of course, the Carnot refrigerator has also dumped $Q_{H}$ Joules of heat in the hot reservoir. But the bottom line is that between them, the super-efficient engine and the Carnot refrigerator have extracted $Δ$ Joules of heat from the hot reservoir and performed $Δ$ Joules of work—contradicting the Second Law.

The Second Law therefore forces the conclusion that no amount of machine design will produce an engine more efficient than the Carnot cycle. The rather low ultimate efficiencies this dictated came as a shock to nineteenth century engineers.

Exercise: prove that it is impossible to construct a reversible engine, operating between two temperatures, that is less efficient than the Carnot cycle. (Hint: hook it to a Carnot cycle, drive one backwards.) It follows that although we used an ideal gas in our analysis, that was unnecessary $—$ the same efficiency would result with any reversible engine operating between the same two temperatures.

previous index next