previous index next PDF Romanian

The Discovery of Energy Conservation: Mayer and Joule

Michael Fowler 6/3/08

Robert Mayer and the Color of Blood

Julius Robert Mayer was born in the mill town of Heilbronn, Germany, on the river Neckar, in 1814. The town’s whole economy was based on water power. The ten year old Mayer had a 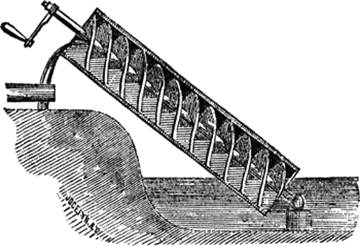great idea: why not use part of a water wheel’s output to drive an Archimedean screw which would pump the water back up again? That way you wouldn’t have to rely on the river at all!

He decided to build a model. His first try didn’t work—some water was pumped back up, but not enough. But surely that could be taken care of by putting in a gear train to make the screw run faster? Disappointingly, he found the water wheel had a tougher time turning the screw faster, and he needed to supply a lot more water over the wheel, so he was back to square one. Increasingly ingenious but unsuccessful fixes finally convinced him that in fact there was no solution: there was no way to arrange a machine to do work for nothing. This lesson stayed with Mayer for life.

Mayer studied to become a medical doctor (his studies included one physics course) and in 1840, at age 25, he signed on as a ship’s doctor on a ship bound for the tropics. Shortly after reaching the Dutch East Indies, some of the sailors became ill and Mayer’s treatment included blood letting. He was amazed to find that the venous blood was a bright red, almost the same as arterial blood. Back in Germany, the venous blood was much darker, and there was a reason: the chemist Lavoisier had explained that the body’s use of food, at least in part, amounted to burning it in a controlled way to supply warmth. The darker venous blood in effect contained the ashes, to be delivered to the lungs and expelled as carbon dioxide. Mayer concluded that less burning of food was needed to keep warm in the tropics, hence the less dark blood.

Now, Lavoisier had claimed that the amount of heat generated by burning, or oxygenation, of a certain amount of carbon did not depend on the sequence of chemical reactions involved, so the heat generated by blood chemistry oxygenation would be the same as that from uncontrolled old-fashioned burning in air. This quantitative formulation led Mayer to think about how he would measure the heat generated in the body, to equate it to the food burned. But this soon led to a problem. Anyone can generate extra heat, just by rubbing the hands together, or, for example, by turning a rusty, unoiled wheel: the axle will get hot. Does this ‘outside’ heat also count as generated by the food? Presumably yes, the food powers the body, and the body generates the heat, even if indirectly. Mayer was convinced from his childhood experience with the water wheel that nothing came from nothing: that outside heat could not just appear from nowhere, it had to have a cause.

But he saw that if the indirectly generated heat must also be included, there is a problem. His analysis ran something like this (I’ve changed the illustration slightly, but the idea’s the same): suppose two people are each steadily turning large wheels at the same rate, and the wheels are equally hard to turn. One of them is our rusty unoiled wheel from the last paragraph, and all that person’s efforts are going into generating heat. But the other wheel has a smooth, oiled axle and generates a negligible amount of heat. It is equally hard to turn, though, because it is raising a large bucket of water from a deep well. How do we balance the ‘food = heat’ budget in this second case?

Mayer was forced to the conclusion that for the ‘food = heat’ equation to make sense, there had to be another equivalence: a certain amount of mechanical work, measured for example by raising a known weight through a given distance, had to count the same as a certain amount of heat, measured by raising the temperature of a fixed amount of water, say, a certain number of degrees. In modern terms, a joule has to be equivalent to a fixed number of calories. Mayer was the first to spell out this ‘mechanical equivalent of heat’ and in 1842 he calculated the number using results of experiments done earlier in France on the specific heats of gases. French experimenters had measured the specific heat of the same gas at constant volume (C_v) and at constant pressure (C_p). They always found C_p to be greater than C_v. Mayer interpreted this with the following thought experiment: consider two identical vertical cylinders, closed at the top by moveable pistons, the pistons resting on the gas pressure, each enclosing the same amount of the same gas at the same temperature. Now supply heat to the two gases, for one gas keep the piston fixed, for the other allow it to rise. Measure how much heat is needed to raise the gas temperature by ten degrees, say. It is found that extra heat is needed for the gas at constant pressure, the one where the piston was allowed to rise. Mayer asserted this was because in that case, some of the heat had been expended as work to raise the piston: this followed very naturally from his previous thinking, and the French measurements led to a numerical value for the equivalence. Mayer understood the sequence: a chemical reaction produces heat and work, that work can then produce a definite amount of heat. This amounted to a statement of the conservation of energy. Sad to report, Mayer was not part of the German scientific establishment, and this ground-breaking work was ignored for some years.

James Joule

Meanwhile, in Manchester, England, the center of the industrial revolution, the same problem was being approached from quite a different direction by James Joule, the son of a prosperous brewer. Joule was lucky in that as a teenager, he was tutored at home, along with his brother, by John Dalton, the chemist who founded the atomic theory. Manchester was at the cutting edge of technological progress, and one exciting idea in the 1830’s was that perhaps coal-driven steam engines could be replaced by battery-driven electric motors. Joule, in his twenties, set himself the task of improving the electric motor to the point where it would be competitive with the steam engine. But it was not to be—after years of effort, he concluded that at best it would take five pounds of zinc consumed in a battery to deliver the work from one pound of coal. But he learned a lot. He found an electric current in a wire produced heat at a rate I²R, now known as Joule heating. The caloric theory interpretation was that caloric fluid originally in the battery was released along with the electric current and settled in the wire. However, Joule discovered the same heating took place with a current generated by moving the wire past a permanent magnet. It was difficult to see how the caloric fluid got into the wire in that situation. Joule decided the caloric theory was suspect. He generated a current by applying a measured force to a dynamo, and established that the heat appearing in the wire was always directly proportional to the work done by the force driving the dynamo.

Finally, it dawned on him that the electrical intermediary was unnecessary: the heat could be produced directly by the force, if instead of turning a dynamo, it turned paddle wheels churning water in an insulated can. The picture below shows his apparatus:

The paddle wheels turn through holes cut in stationary brass sheets, churning up the water. This is all inside an insulated can, of course. In this way, Joule measured the mechanical equivalent of heat, the same number Mayer had deduced from the French gas experiments.

Joule’s initial reception by the scientific establishment was not too different from Mayer’s. He, too, was a provincial, with a strange accent. But he had a lucky break in 1847, when he reported his work to a meeting of the British Association, and William Thomson was in the audience. Thomson had just spent a year in Paris. He was fully familiar with Carnot’s work, and believed the caloric theory to be correct. But he knew that if Joule really had produced heat by stirring water, the caloric theory must be wrong—he said there were ‘insuperable difficulties’ in reconciling the two.

But Who Was First: Mayer or Joule?

Mayer and Joule, using entirely different approaches, arrived almost simultaneously at the conclusion that heat and mechanical work were numerically equivalent: a given amount of work could be transformed into a quantitatively predictable amount of heat. Which of the two men deserves more credit (not to mention other contenders!) has been argued for well over a century. Briefly, it is generally conceded that Mayer was the first to spell out the concept of the mechanical equivalent of heat (although closely followed, independently, by Joule) and Joule was the first to put it on a firm experimental basis.

The Emergence of Energy Conservation

In fact, by the 1840’s, although many still believed in the caloric theory, it had run into other difficulties. Before the 1820’s, almost everyone believed, following Newton, that light was a stream of particles. Around 1800, Herschel discovered that on passing sunlight through a prism, and detecting the heat corresponding to the different colors, in fact there was heat transmitted beyond the red. This suggested that radiant heat was caloric particles streaming through space, and no doubt very similar in character to light. But in the 1820’s it was unambiguously established that light was really a wave. Did this mean heat was a wave too? Perhaps the caloric fluid was oscillations in the ether. Things were now very confused. In 1841, Joule wrote diplomatically: ‘let the space between these compound atoms be supposed to be filled with calorific ether in a state of vibration, or, otherwise, to be occupied with the oscillations of the atoms themselves’ (Joule 1963, p.52).

It transpired, though, that the difficulties in reconciling Carnot’s theory and Joule’s experiments were not as insuperable as Thomson had claimed. In 1850, a German professor, Rudolph Clausius, pointed out that Carnot’s theory was still almost right: the only adjustment needed was that there was a little less heat emerging from the bottom of the ‘caloric water wheel’ than went in at the top—some of the heat became mechanical energy, the work the steam engine was performing. For real steam engines, the efficiency—the fraction of ingoing heat delivered as useful work—was so low that it was easy to understand why Carnot’s picture had been accepted for so long. For the first time, with Clausius’ paper, a coherent theory of heat emerged, and the days of the caloric theory drew to a close.

Books I used in writing these notes…

Caneva, K. L.: 1993, Robert Mayer and the Conservation of Energy, Princeton University Press, Princeton, New Jersey.

Cardwell, D. S. L.: 1989, James Joule: A Biography, Manchester University Press, Manchester and New York.

Cardwell, D. S. L.: 1971, From Watt to Clausius, Cornell University Press, Ithaca, New York.

Joule, J. P.: 1963, Scientific Papers, Vol. I, Dawsons of Pall Mall, London.

Magie, W. F.: 1935, A Source Book in Physics, McGraw-Hill, New York.

Roller, D.: 1957, ‘The Early Development of the Concepts of Temperature and Heat: The Rise and Decline of the Caloric Theory’, in J. B. Conant and L. K. Nash (eds.), Harvard Case Histories in Experimental Science, Harvard University Press, Cambridge, Massachusetts, 1957, 117-215.