University of Virginia
Physics 252 Home Page
Link to Previous Lecture
[Rutherford was] a "tribal chief", as a student
said.
(Richard Rhodes, The Making of the Atomic Bomb,
page 46)
In 1908 Rutherford was awarded the Nobel Prize - for chemistry! The
award citation read: "for his investigations into the disintegration
of the elements, and the chemistry of radioactive substances." While
at McGill University, he had discovered that the radioactive element thorium
emitted a gas which was itself radioactive, but if the gas radioactivity
was monitored separately from the thorium's, he found it decreased geometrically,
losing approximately half its current strength for each minute that passed.
The gas he had found was a short-lived isotope of radon, and this was the
first determination of a "half-life" for a radioactive material.
(Pais, IB, page 120)
The chemists were of course impressed that Rutherford was fulfilling
their ancient alchemical dream of transmuting elements, or at least demonstrating
that it happened. Rutherford himself remarked at the ceremony that he "had
dealt with many different transformations with various time-periods, but
the quickest he had met was his own transformation from a physicist to
a chemist". Still, Nobel prizes of any kind are nice to get, so he
played along, titling his official Nobel lecture: "The chemical nature
of the alpha-particle from radioactive substances". (He established
that his favorite particle was an ionized helium atom by collecting alphas
in an evacuated container, where they picked up electrons. After compressing
this very rarefied gas, he passed an electric discharge through it and
observed the characteristic helium spectrum in the light emitted.)
Rutherford was the world leader in alpha-particle physics. In 1906,
at McGill, he had been the first to detect slight deflections of alphas
on passage through matter. In 1907, he became a professor at the University
of Manchester, where he worked with Hans Geiger. This was just a year after
Rutherford's old boss, J. J. Thomson, had written a paper on his plum pudding
atomic model suggesting that the number of electrons in an atom was about
the same as the atomic number. (Not long before, people had speculated
that atoms might contain thousands of electrons. They were assuming that
the electrons contributed a good fraction of the atom's mass.) The actual
distribution of the electrons in the atom, though, was as mysterious as
ever. Mayer's magnets were fascinating, but had not led to any quantitative
conclusions on electronic distributions in atoms.
Rutherford's 1906 discovery that his pet particles were slightly deflected
on passing through atoms came about when he was finding their charge to
mass ratio, by measuring the deflection in a magnetic field. He detected
the alphas by letting them impact photographic film. When he had them pass
through a thin sheet of mica before hitting the film (so the film didn't
have to be in the vacuum?) he found the image was blurred at the edges,
evidently the mica was deflecting the alphas through a degree or two. He
also knew that the alphas wouldn't be deflected a detectable amount by
the electrons in the atom, since the alphas weighed 8,000 times
as much as the electrons, atoms contained only a few dozen electrons, and
the alphas were very fast. The mass of the atom must be tied up somehow
with the positive charge. Therefore, he reasoned, analyzing these small
deflections might give some clue as to the distribution of positive charge
and mass in the atom, and therefore give some insight into his old boss
J. J.'s plum pudding. The electric fields necessary in the atom for the
observed scattering already seemed surprisingly high to Rutherford (Pais,
page 189).
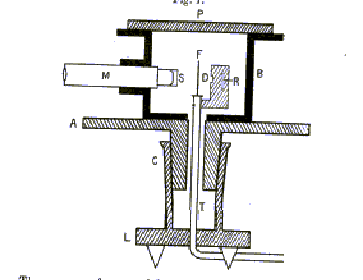
Rutherford's alpha scattering experiments were the first experiments
in which individual particles were systematically scattered and detected.
This is now the standard operating procedure of particle physics. To minimize
alpha loss by scattering from air molecules, the experiment was carried
out in a fairly good vacuum, the metal box being evacuated through a tube
T (see below). The alphas came from a few milligrams of radium (to be precise,
its decay product radon 222) at R in the figure below, from the original
paper, which goes on: "By means of a diaphragm placed at D, a pencil
of alpha particles was directed normally on to the scattering foil F. By
rotating the microscope [M] the alpha particles scattered in different
directions could be observed on the screen S." Actually, this was
more difficult than it sounds. A single alpha caused a slight fluorescence
on the zinc sulphide screen S at the end of the microscope. This could
only be reliably seen by dark-adapted eyes (after half an hour in complete
darkness) and one person could only count the flashes accurately for one
minute before needing a break, and counts above 90 per minute were too
fast for reliability. The experiment accumulated data from hundreds of
thousands of flashes.
Rutherford's partner in the initial phase of this work was Hans Geiger, who later developed the Geiger counter to detect and count fast particles. Many hours of staring at the tiny zinc sulphide screen in the dark must have focused his mind on finding a better way!

In 1909, an undergraduate, Ernest Marsden, was being trained by Geiger.
To quote Rutherford (a lecture he gave much later):
"I had observed the scattering of alpha-particles, and Dr. Geiger in my laboratory had examined it in detail. He found, in thin pieces of heavy metal, that the scattering was usually small, of the order of one degree. One day Geiger came to me and said, "Don't you think that young Marsden, whom I am training in radioactive methods, ought to begin a small research?" Now I had thought that, too, so I said, " Why not let him see if any alpha-particles can be scattered through a large angle?" I may tell you in confidence that I did not believe that they would be, since we knew the alpha-particle was a very fast, massive particle with a great deal of energy, and you could show that if the scattering was due to the accumulated effect of a number of small scatterings, the chance of an alpha-particle's being scattered backward was very small. Then I remember two or three days later Geiger coming to me in great excitement and saying "We have been able to get some of the alpha-particles coming backward …" It was quite the most incredible event that ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."
The back scattered alpha-particles proved fatal to the plum pudding
model. A central assumption of that model was that both the positive charge
and the mass of the atom were more or less uniformly distributed over its
size, approximately 10-10 meters across or a little more. It
is not difficult to calculate the magnitude of electric field from this
charge distribution. (Recall that this is the field that must scatter the
alphas, the electrons are so light they will jump out of the way with negligible
impact on an alpha.)
To be specific, let us consider the gold atom, since the foil used by
Rutherford was of gold, beaten into leaf about 400 atoms thick. The gold
atom has a positive charge of 79e (balanced of course by that of the 79
electrons in its normal state). Neglecting these electrons -- assume them
scattered away -- the maximum electric force the alpha will encounter is
that at the surface of the sphere of positive charge,
If the alpha particle initially has momentum p, for small deflections
the angle of deflection (in radians) is given by (delta_p)/p,
where delta_p is the sideways momentum resulting from the electrically
repulsive force of the positive sphere of charge. Assuming the atomic sphere
itself moves negligibly -- it is much heavier than the alpha, so this is
reasonable -- the trajectory of the alpha in the inverse square electric
field can be found by standard methods. It is the same mathematical problem
as finding the elliptic orbits of planets around the sun. Replacing inverse
square attraction with inverse square repulsion changes the orbit from
an ellipse (or a hyperbola branch swinging around the sun for a comet)
to a hyperbola branch lying on one side of the center of repulsion.
In fact, one can get a clear idea of how much deflection comes about
without going into the details of the trajectory. Outside the atom, the
repulsive electrical force falls away as the inverse square. Inside the
atom, the force drops to zero at the center, just as the gravitational
force is zero at the center of the earth. The force is maximum right at
the surface. Therefore, a good idea of the sideways deflection is given
by assuming the alpha experiences that maximal force for a time interval
equal to the time it takes the alpha to cross the atom -- say, a distance
2r0.
Note that since the alpha particle has mass 6.7x10-27 kg,
from F = ma, the electric force at the atomic surface above
will give it a sideways acceleration of 5.4x1020 meters per
sec per sec (compare g = 10!). But the force doesn't have long to
act - the alpha is moving at 1.6x107 meters per second. So the
time available for the force to act is the time interval a particle needs
to cross an atom if the particle gets from New York to Australia in one
second.
The time t0 = 2r0/v = 2x10-10/1.6x107
= 1.25x10-17 seconds.
Thus the magnitude of the total sideways velocity picked up is the sideways acceleration multiplied by
the time,
1.25x10-17x5.4x1020 = 6750 meters per second.
This is a few ten-thousandths of the alpha's forward speed, so there is only a very tiny deflection. Even if the alpha hit 400 atoms in succession and they all deflected it the same way, an astronomically improbable event, the deflection would only be of order a degree. Therefore, the observed deflection through ninety degrees and more was completely inexplicable using Thomson's pudding model!
Rutherford pondered the problem for some months. He had been a believer
in his former boss's pudding model, but he eventually decided there was
simply no way it could generate the strength of electric field necessary
to deflect the fast moving alphas. Yet it was difficult to credit there
was much more positive charge around than that necessary to compensate
for the electrons, and it was pretty well established that there were not
more than a hundred or so electrons (we used 79, the correct value -- that
was not known exactly until a little later). The electric field from a
sphere of charge reaches its maximum on the surface, as discussed above.
Therefore, for a given charge, assumed spherically distributed, the only
way to get a stronger field is to compress it into a smaller sphere.
Rutherford concluded that he could only explain the large alpha deflections
if the positive charge, and most of the mass of the atom, was in a sphere
much smaller than the atom itself.
It is not difficult to estimate from the above discussion how small
such a nucleus would have to be to give a substantial deflection.
We found a sphere of radius 10-10 meters gave a deflection of
about 4x10-4 radians. We need to increase this deflection by
a factor of a few thousand. On decreasing the radius of the sphere of positive
charge, the force at the surface increases as the inverse radius squared.
On the other hand, the time over which the alpha experiences the
sideways force decreases as the radius. The total deflection,
then, proportional to the product of force and time, increases as the
inverse of the radius. This forces the conclusion that the positive
charge is in a sphere of radius certainly less than 10-13 meters,
provided all the observed scattering is caused by one encounter with a
nucleus.
Rutherford decided that the observed scattering was in fact from a single nucleus. He argued as follows: since the foil is only 400 atoms thick, it is difficult to see how ninety degree scatterings could arise unless the scattering by a single nucleus was at least one degree, say 100 times that predicted by the Thomson model. This would imply that the nucleus had a radius at most one-hundredth that of the atom, and therefore presented a target area for one-degree scattering (or more) to the incoming alphas only one ten-thousandth that of the atom. (In particle physics jargon, this target area is called the scattering cross section.) If an alpha goes through 400 layers of atoms, and in each layer it has a chance of one in ten thousand of getting close enough to the nucleus for a one-degree scatter, this is unlikely to happen twice. It follows that almost certainly only one scattering takes place. It then follows that all ninety or more degrees of scattering must be a single event, so the nucleus must be even smaller than one hundredth the radius of the atom -- it must be less than 10-13 meters, as stated above.
To visualize the path of the alpha in such a scattering, Rutherford "had a model made, a heavy electromagnet suspended as a pendulum on thirty feet of wire that grazed the face of another electromagnet set on a table. With the two grazing faces matched in polarity and therefore repelling each other, the pendulum was deflected" into a hyperbolic path.(Rhodes, page 50) In place of this rather substantial model, I've put in two applets, showing alphas deflected by two spheres of charge having the same total charge, but different radii. The large sphere, then, represents the Thomson model, the smaller one a nuclear model. These are of course not to scale! An accurate nuclear representation would take far less than one pixel, and hours between significant scatterings. Nevertheless, the relation between large angle scattering and the size of the positive sphere is clear from the model.
Having decided that the observed scattering of the alphas came from
single encounters with nuclei, and assuming that the scattering force was
just the electrostatic repulsion, Rutherford realized that finding the
scattering angle as a function of ingoing speed and impact parameter
(how close to the center would the alpha particle pass if the repulsion
were switched off) was an exercise in Newtonian mechanics. Although not
exactly a hot shot theorist, Rutherford managed to figure this out after
a few weeks. Anyway, the bottom line is that for a nucleus of charge Z,
and incident alpha particles of mass m and speed v, the rate
of scattering to a point on the screen corresponding to a scattering angle
of theta (angle between incident velocity and final velocity of
alpha) is proportional to:
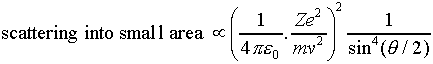
Analysis of the hundred thousand or more scattering events recorded
for the alphas on gold fully confirmed the angular dependence predicted
by the above analysis.
But it didn't work for aluminum! On replacing the gold foil by aluminum foil (some years later), it turned out that small angle scattering obeyed the above law, but large angle scattering didn't. Rutherford correctly deduced that in the large angle scattering, which corresponded to closer approach to the nucleus, the alpha was actually hitting the nucleus. This meant that the size of the nucleus could be worked out by finding the maximum angle for which the inverse square scattering formula worked, and finding how close to the center of the nucleus such an alpha came. Rutherford estimated the radius of the aluminum nucleus to be about 10-14 meters.
The First World War lasted from 1914 to 1918. Geiger and Marsden were
both at the Western front, on opposite sides. Rutherford had a large water
tank installed on the ground floor of the building in Manchester, to carry
out research on defense against submarine attack. Nevertheless, occasional
research on alpha scattering continued. Scattering from heavy nuclei was
fully accounted for by the electrostatic repulsion, so Rutherford concentrated
on light nuclei, including hydrogen and nitrogen. In 1919, Rutherford established
that an alpha impinging on a nitrogen nucleus can cause a hydrogen
atom to appear! Newspaper headlines blared that Rutherford had "split
the atom". (Rhodes, page 137)
Shortly after that experiment, Rutherford moved back to Cambridge to
succeed J. J. Thomson as head of the Cavendish laboratory, working with
one of his former students, Chadwick, who had spent the war years interned
in Germany. They discovered many unusual effects with alpha scattering
from light nuclei. In 1921, Chadwick and co-author Bieler wrote: "The
present experiments do not seem to throw any light on the nature of the
law of variation of the forces at the seat of an electric charge, but merely
show that the forces are of great intensity … It is our task to find some
field of force which will reproduce these effects." I took this quote
from Pais, page 240, who goes on to say that he considers this 1921 statement
as marking the birth of the strong interactions.
In fact, Rutherford was beginning to focus his attention on the actual
construction of the nucleus and the alpha particle. He coined the word
"proton" to describe the hydrogen nucleus, it first appeared
in print in 1920 (Pais). At first, he thought the alpha must be made up
of four of these protons somehow bound together by having two electrons
in the middle - this would get the mass and charge right, but of course
nobody could construct a plausible electrostatic configuration. Then he
had the idea that maybe there was a special very tightly bound state of
a proton and an electron, much smaller than an atom. By 1924, he and Chadwick
were discussing how to detect this neutron. It wasn't going to be easy
- it probably wouldn't leave much of a track in a cloud chamber. In fact,
Chadwick did discover the neutron, but not until 1932, and it wasn't much
like their imagined proton-electron bound state. But it did usher in the
modern era in nuclear physics.
Physics 252 Home Page
Link to Next Lecture