


Next: Sound waves
Up: Compressible fluids
Previous: Compressible fluids
When the density 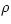 changes, both the pressure p and the temperature T will change, in general. The usual way to describe these changes in
thermodynamics is to change the volume V occupied by a fixed number N of
particles, so that
changes, both the pressure p and the temperature T will change, in general. The usual way to describe these changes in
thermodynamics is to change the volume V occupied by a fixed number N of
particles, so that
| 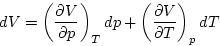 |
(2) |
It is convenient to consider the
fractional volume change dV/V and to define the isothermal
compressibility
| 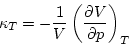 |
(3) |
and the thermal expansion coefficient

which are positive quantities characteristic of the material (fluid or
solid). To convert from dV/V to a change of density, we note that a fixed N implies that 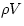 is a constant (it is the mass contained in V).
Then
is a constant (it is the mass contained in V).
Then 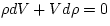 and we get
and we get
|  |
(4) |
As an example, consider an ideal gas. From pV=NkBT, get pdV+Vdp=NkBdT, hence
|  |
(5) |
|  |
(6) |
As we said already, there are two limiting cases where heat transfer and
fluid motions are effectively decoupled, and then the dynamics of the fluid
is fully determined by the appropriate compressibility coefficient:
- If the density changes slowly, so that heat conduction keeps the
temperature T constant, eq. (5.4) reduces to
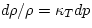 , where
, where 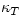 is the isothermal compressibility (5.3). As we have already noted,
is the isothermal compressibility (5.3). As we have already noted, 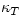 is positive (because a
compression corresponds to a positive dp and a negative dV), and does
not depend on the size of V (because for a larger V we get a
correspondingly larger dV for the same dp). However,
is positive (because a
compression corresponds to a positive dp and a negative dV), and does
not depend on the size of V (because for a larger V we get a
correspondingly larger dV for the same dp). However, 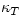 can
depend on p and on the temperature T. For example, in an ideal gas,
can
depend on p and on the temperature T. For example, in an ideal gas, 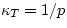 .
. - If the density changes rapidly, so that no heat can flow, we have
instead
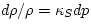 , where
, where
 |
(7) |
is the adiabatic compressibility, which we now discuss. The subscript S denotes a process at constant entropy, in accordance with the fact that
an adiabatic volume change (dQ=0, no heat transfer) is also isentropic (dS=0). In such a process all the work done in changing the volume goes into
the internal energy E of the fluid and eq. (5.1) reduces to
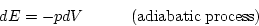
This condition allows us to compute 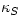 . For example, in an ideal
gas dE=CVdT, hence for an adiabatic process CVdT = -pdV.
Using this result in eq. (5.5), we find (1 + NkB)pdV + Vdp = 0
and by the definition (5.8):
. For example, in an ideal
gas dE=CVdT, hence for an adiabatic process CVdT = -pdV.
Using this result in eq. (5.5), we find (1 + NkB)pdV + Vdp = 0
and by the definition (5.8):
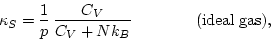
Recalling that Cp=CV+NkB is the specific heat at constant pressure![[*]](http://www.phys.virginia.edu/usr/icons.gif/foot_motif.gif) and comparing with
equation (5.5), we see that
and comparing with
equation (5.5), we see that
|  |
(8) |
This relation is true in general (as can be proved by thermodynamics). It is
almost always true that Cp>CV, so that 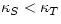 : it
is harder to compress a fluid if heat does not flow out of it.
: it
is harder to compress a fluid if heat does not flow out of it.
In a typical liquid, there is little difference between 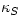 and
and 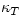 , but in a monatomic ideal gas the difference is large: CV=(3/2)NkB and Cp=(5/2)NkB. The ratio Cp/CV appears
often in the physics of gases and is called
, but in a monatomic ideal gas the difference is large: CV=(3/2)NkB and Cp=(5/2)NkB. The ratio Cp/CV appears
often in the physics of gases and is called 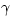 . For a monatomic ideal
gas,
. For a monatomic ideal
gas,  ; for air near room temperature
; for air near room temperature 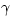 is very
close to 1.4, which is the value for a diatomic ideal gas when the molecules
can be regarded as rigid (at higher temperatures, molecular vibrations
increase CV, so that
is very
close to 1.4, which is the value for a diatomic ideal gas when the molecules
can be regarded as rigid (at higher temperatures, molecular vibrations
increase CV, so that 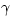 decreases).
decreases).
The inverse of the compressibility coefficient is called the bulk
modulus B. We can define 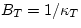 and
and 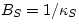 ,
but we can use simply B and let the context distinguish what we mean
(keeping in mind that for liquids, and solids, the distinction is
unimportant). We also want to relate pressure changes to density changes,
rather than volume changes. Using rdV + Vdr = 0
as in the derivation of eq. (5.4), we see that
,
but we can use simply B and let the context distinguish what we mean
(keeping in mind that for liquids, and solids, the distinction is
unimportant). We also want to relate pressure changes to density changes,
rather than volume changes. Using rdV + Vdr = 0
as in the derivation of eq. (5.4), we see that
| 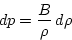 |
(9) |
Values of 1/B are given in Table 7.16 of PQRG. We see that for
common organic liquids B is about 1 GigaPascal (10 N/m2),
increasing slowly with pressure. Water is a little less compressible:
N/m2),
increasing slowly with pressure. Water is a little less compressible: 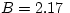 GPa at
GPa at 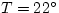 C and
C and 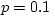 MPa. Mercury is a lot less
compressible: with
MPa. Mercury is a lot less
compressible: with 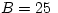 GPa it is getting close to the range of solid
metals.
GPa it is getting close to the range of solid
metals.



Next: Sound waves
Up: Compressible fluids
Previous: Compressible fluids
Vittorio Celli
11/10/1997
![]() changes, both the pressure p and the temperature T will change, in general. The usual way to describe these changes in
thermodynamics is to change the volume V occupied by a fixed number N of
particles, so that
changes, both the pressure p and the temperature T will change, in general. The usual way to describe these changes in
thermodynamics is to change the volume V occupied by a fixed number N of
particles, so that
![]()
![]()
![]()
![]() and
and ![]() , but in a monatomic ideal gas the difference is large: CV=(3/2)NkB and Cp=(5/2)NkB. The ratio Cp/CV appears
often in the physics of gases and is called
, but in a monatomic ideal gas the difference is large: CV=(3/2)NkB and Cp=(5/2)NkB. The ratio Cp/CV appears
often in the physics of gases and is called ![]() . For a monatomic ideal
gas,
. For a monatomic ideal
gas, ![]() ; for air near room temperature
; for air near room temperature ![]() is very
close to 1.4, which is the value for a diatomic ideal gas when the molecules
can be regarded as rigid (at higher temperatures, molecular vibrations
increase CV, so that
is very
close to 1.4, which is the value for a diatomic ideal gas when the molecules
can be regarded as rigid (at higher temperatures, molecular vibrations
increase CV, so that ![]() decreases).
decreases).
![]() and
and ![]() ,
but we can use simply B and let the context distinguish what we mean
(keeping in mind that for liquids, and solids, the distinction is
unimportant). We also want to relate pressure changes to density changes,
rather than volume changes. Using rdV + Vdr = 0
as in the derivation of eq. (5.4), we see that
,
but we can use simply B and let the context distinguish what we mean
(keeping in mind that for liquids, and solids, the distinction is
unimportant). We also want to relate pressure changes to density changes,
rather than volume changes. Using rdV + Vdr = 0
as in the derivation of eq. (5.4), we see that
![]() N/m2),
increasing slowly with pressure. Water is a little less compressible:
N/m2),
increasing slowly with pressure. Water is a little less compressible: ![]() GPa at
GPa at ![]() C and
C and ![]() MPa. Mercury is a lot less
compressible: with
MPa. Mercury is a lot less
compressible: with ![]() GPa it is getting close to the range of solid
metals.
GPa it is getting close to the range of solid
metals.