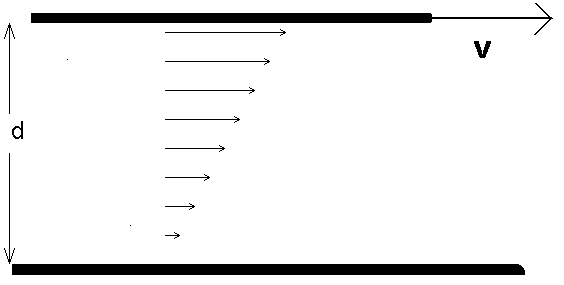
Figure 3.1: Viscous drag between two plates; the bottom plate is held fixed.
When we deform a solid, so that it is strained, we know that the solid will exert a restoring force which opposes the strain; for small strains the restoring force is proportional to the strain, and we have the familiar Hooke's Law. Real fluids also oppose strains; however, in a fluid it is not the amount of strain which is important but the rate at which the strain is produced. For instance, if you were to draw a utensil through your favorite viscous fluid (maple syrup, say), you would find that it was easy for slow motions of the utensil, but more difficult if the utensil is moved rapidly. A simple fluid flow is shown in Fig. 3.1.

Figure 3.1: Viscous drag between two plates; the bottom plate is held fixed.
If the force per unit area of the top plate is measured, we would find
with d the separation between the plates. This essentially defines the
viscosity ![]() (sometimes called the shear viscosity). Note that we
haven't derived this law--it is a consequence of experimental observation,
just like Ohm's law, Fourier's law and Fick's law. A fluid which responds to
a shear stress F/A in this manner is called a Newtonian fluid ; it has the property that the viscosity is
independent of velocity. Most of the fluids that we will be interested in
will be Newtonian (air, water). Non-Newtonian fluids (Silly-Putty, paint,
polymeric fluids) are more complicated and beyond the scope of the present
description. Some typical fluid viscosities are given in Table 3.1 and on pages 133-135 of PQRG. Also listed in Table 3.1 are the kinematic viscosities
(sometimes called the shear viscosity). Note that we
haven't derived this law--it is a consequence of experimental observation,
just like Ohm's law, Fourier's law and Fick's law. A fluid which responds to
a shear stress F/A in this manner is called a Newtonian fluid ; it has the property that the viscosity is
independent of velocity. Most of the fluids that we will be interested in
will be Newtonian (air, water). Non-Newtonian fluids (Silly-Putty, paint,
polymeric fluids) are more complicated and beyond the scope of the present
description. Some typical fluid viscosities are given in Table 3.1 and on pages 133-135 of PQRG. Also listed in Table 3.1 are the kinematic viscosities ![]() .
Recall that 1 pascal equals 1 kg·m-1s-2 and note that the viscosity of water is, conveniently, 1 mPa·s = 1 g·m-1s-1; it is common to quote relative viscosities, which are viscosities relative to water, or in mPa·s, and also to use the cgs unit of viscosity, g·cm-1s-1, called the poise (after Poiseuille) and equal to 0.1 Pa·s.
.
Recall that 1 pascal equals 1 kg·m-1s-2 and note that the viscosity of water is, conveniently, 1 mPa·s = 1 g·m-1s-1; it is common to quote relative viscosities, which are viscosities relative to water, or in mPa·s, and also to use the cgs unit of viscosity, g·cm-1s-1, called the poise (after Poiseuille) and equal to 0.1 Pa·s.
| Fluid | Viscosity | Kinematic viscosity n |
| Air ( | 1.7 × 10-5 Pa·s | 1.32 × 10-5 m2s-1 |
|
Air ( | | |
|
Water ( | | |
|
Water ( | | |
|
Glycerin ( | 1.4 | 1.1 ×10-3 |
| Blood (37°C) | 4.0 ×10-3 |
Before incorporating viscosity into the equations of fluid mechanics, let's take a moment to discuss some of the properties of viscosity. Viscosity does not depend upon pressure in a significant way, but you know from personal experience that it does depend upon temperature--pancake syrup becomes less viscous after you take it out of the refrigerator and let it warm up. Generally, the viscosity of liquids decreases with increasing temperature. Gases, on the other hand, have viscosities which generally increase with increasing temperature. Why the difference?
Viscosity is fundamentally a consequence of the intermolecular interactions in the fluid. In a dilute gas you can think in terms of binary collisions of pairs of molecules. Now viscosity is the transfer of momentum from one part of a fluid to an adjacent part, and in a dilute gas this transfer will be more effective if the collisions are very energetic. Since the mean kinetic energy of a molecule is (3/2)kBT, higher temperatures imply a larger viscosity for a gas. A liquid, on the other hand, is a strongly interacting collection of molecules, and the idea of a binary collision is meaningless. Microscopically the molecules in a liquid do have some short range order--a given molecule is surrounded by a "cage'' of other molecules. Momentum transfer in the liquid will involve the movement of these cages around one another. Increasing the temperature causes the cages to jiggle a bit more, allowing them to slip more easily past one another, thereby reducing the momentum transfer between adjacent bits of the fluid, and thereby reducing the viscosity of the liquid. More detail than this requires kinetic theory.