The stress tensor and the Navier-Stokes equation

The velocity of a fluid will vary in a complicated way in space; however, we can still apply the above definition of viscosity to a bit of fluid of thickness with an infinitesimal area . The shear stress across the thickness is

 

We can further generalize and define the xy component of the viscous stress tensor as

 

The notation is made clearer in Fig. 3.2. This definition ensures that for a uniform rotation of the fluid there are no viscous stresses. ¹
  

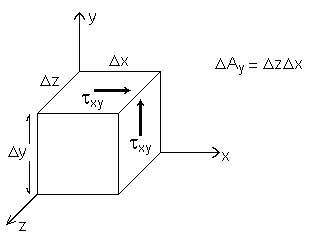
Figure 3.2: Stresses acting on a small cube.

We can apply the same arguments as above to other flow configurations, with the result that the viscous stress tensor is given by

 

where i,j=(x,y,z). ². Now in a fluid we can have internal stresses due to the fluid pressure p in addition to the stress due to viscous forces; the total stress tensor in the fluid is then

 

where is the Kronecker delta, defined such that if i=j, and otherwise. Once we have the stress tensor, the force per unit volume of the fluid is obtained by considering the stresses acting upon an infinitesimal cube of the fluid, and calculating the net force on the cube by taking the differences in the stress acting on different faces (just like our calculation of the force arising from pressure gradients in the fluid). This results in derivatives of the stress tensor, so that the ith component of the force per unit volume is

 

If we work out this last sum, we find (assuming that the viscosity doesn't depend on position)

 

For an incompressible fluid ; reinstating vector notation, we see that the sum is then just , so that the force per unit volume is

 

This is the force which goes into Newton's Second Law in order to obtain the equation of motion for :

 

This is the Navier-Stokes equation for an incompressible fluid. Along with the equation of continuity, it is the basic equation which governs the flow of Newtonian fluids.

To complete the description of the flow we need to specify the boundary conditions on the velocity field at a solid surface. In our dealings with nonviscous flow we imposed the condition that the normal component of the fluid velocity at a solid surface must be zero -- this just ensures that no fluid flows through the surface. Once we deal with real (viscous) fluids, we must also require that the tangential component of the velocity of the fluid be zero on the surface. This condition is often called the no-slip boundary condition, and is the result of experimental observations.

Footnotes:

¹ To see this, notice that a fluid in uniform rotation with angular velocity W will have a velocity field given by v = W×r, with r the displacement vector from the center of rotation. If the z axis is the rotation axis, then v_x = -Wy, v_y = Wx and we see that t_xy = 0.
² This is the general result for an incompressible fluid; for compressible fluids there is a second viscosity, often labeled z, which will enter into the viscosity stress tensor. Since our discussion of fluid mechanics is confined to incompressible fluids for the moment, we will drop this term.