Lecture 1, Jan 21, 99
Review of electrostatics: Coulomb's law, relation of field to potential, E = - ÑV. Charge distribution on insulators and conductors.
Assigned reading (by next Thursday): Bloomfield, section 11.1
Assigned problem set 1
References:
Problem session 1
Given hints on solving problem set 1, using MAPLE to do the plots. Handed out MAPLE help sheet.
Lecture 2, Jan 26
Continued review of electrostatics: Ñ × E = 0,
Ñ · E = r/e0 (or
Ñ · E = 4pr in gaussian units)
and Poisson's equation Ñ2V = - r/e0 (or
Ñ2V = - 4pr in gaussian units).
In charge-free space ![]() (Laplace's equation). Analogy of electric field to fluid velocity for an
incompressible, non-viscous fluid. Dipole moment; field of a dipole, force on a dipole (proportional to field gradient). Induced dipole on a conducting sphere and on a molecule. Electrical discharges.
(Laplace's equation). Analogy of electric field to fluid velocity for an
incompressible, non-viscous fluid. Dipole moment; field of a dipole, force on a dipole (proportional to field gradient). Induced dipole on a conducting sphere and on a molecule. Electrical discharges.
References:
Demos: discharges from domes and a sharp point; Jacob's ladder (effect of previous discharges); precipitating smoke particles.
The electric potential of a dipole of strength p pointing in the z direction is
Vdip = k pz/r3, where
k = 1/4pe0 in SI (k = 1 in gaussian units).
This can be rewritten as Vdip = k pcosq/r2, where q is the angle from the z axis.
If a conducting sphere of radius a is placed in a uniform electric field E0, a dipole moment p = (1/k)E0 a3 is induced on the sphere.
A uniform field in the z direction is described by the potential
V0 = - E0 z. The total potential for the sphere in the uniform
field is then
Assigned problem set 2.
References:
Problem session 2
Solutions to problem set 1. Given hints on solving set 2 and getting pretty plots with MAPLE. See example at http://erwin.phys.virginia.edu/~jsf9k/hints.html. See also MAPLE short course notes, on reserve.
Lecture 4, Feb 2
Demos: shown "insides" of electrostatic air cleaner and laser printer.
Uniqueness of solution of Laplace's equation,
![]() , with assigned vaues
of V on the boundary (in practice, V has assigned values on various conductors).
How to proceed if the charges on the conductors are given, instead of the values of the potential.
Simplest example: Q = C(V1 - V2) for a capacitor with charges +Q and -Q
on the plates at potentials V1 and V2. C is the capacitance.
, with assigned vaues
of V on the boundary (in practice, V has assigned values on various conductors).
How to proceed if the charges on the conductors are given, instead of the values of the potential.
Simplest example: Q = C(V1 - V2) for a capacitor with charges +Q and -Q
on the plates at potentials V1 and V2. C is the capacitance.
Started review of quantum theory:
What is quantized and when? In periodic motion, action is quantized in units of h;
as a consequence, other quantities are quantized too, but not so simply.
What is action? It is a quantity with dimensions ML2T-1;
it can be energy × time, or momentum × length. Angular momentum has the same dimensions as action
and is simply quantized in units of 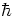 .
.
What is spin? It is something like the internal angular momentum of an elementary particle.
However, electrons (and quarks) have spin 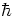 /2, while orbital angular momentum must be an
integer multiple of
/2, while orbital angular momentum must be an
integer multiple of 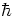 .
Photons have spin
.
Photons have spin 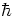 . One often says that electrons have spin 1/2 and photons
have spin 1.
. One often says that electrons have spin 1/2 and photons
have spin 1.
What is the Pauli exclusion principle? Read about it in Serway, page 860, or Tipler,
page 1206 and 1234, as it applies
to electrons. Actually, it applies to all elementary particles with spin 1/2 (called fermions) and is
mysteriously related to their unusual spin. It also applies to composite particles with half-integer spin
(1/2, 3/2, etc.).
References:
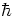 , so that some formulas look a little different. Physics
articles today almost always use
, so that some formulas look a little different. Physics
articles today almost always use 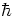 , unless they use "atomic units" in
which
, unless they use "atomic units" in
which 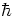 is set equal to 1. See last semester's
lecture on
atomic units.
is set equal to 1. See last semester's
lecture on
atomic units.Lecture 5, Feb 4
Review of quantum mechanics: action, phase,
sum over all possible paths with a phase factor, uncertainty principle,
spin and the Pauli exclusion principle, plane wave solution of
the time-dependent Schrodinger equation,
E = hf = 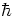 w and
p =
w and
p = 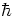 k.
k.
Assigned problem set 3 (engineering of electrostatic precipitator, basic quantum theory).