previous index next
Linear Algebra for Quantum Mechanics
Michael Fowler, UVa
Introduction
We’ve seen that in quantum mechanics, the state of an electron in some potential is given by a wave function , and physical variables are represented by operators on this wave function, such as the momentum in the -direction The Schrödinger wave equation is a linear equation, which means that if and are solutions, then so is , where are arbitrary complex numbers.
This linearity of the sets of possible solutions is true generally in quantum mechanics, as is the representation of physical variables by operators on the wave functions. The mathematical structure this describes, the linear set of possible states and sets of operators on those states, is in fact a linear algebra of operators acting on a vector space. From now on, this is the language we’ll be using most of the time. To clarify, we’ll give some definitions.
What is a Vector Space?
The prototypical vector space is of course the set of real vectors in ordinary three-dimensional space, these vectors can be represented by trios of real numbers measuring the components in the and directions respectively.
The basic properties of these vectors are:
any vector multiplied by a number is another vector in the space, ;
the sum of two vectors is another vector in the space, that given by just adding the corresponding components together:
These two properties together are referred to as “closure”: adding vectors and multiplying them by numbers cannot get you out of the space.
A further property is that there is a unique null vector and each vector has an additive inverse which added to the original vector gives the null vector.
Mathematicians have generalized the definition of a vector space: a general vector space has the properties we’ve listed above for three-dimensional real vectors, but the operations of addition and multiplication by a number are generalized to more abstract operations between more general entities. The operators are, however, restricted to being commutative and associative.
Notice that the list of necessary properties for a general vector space does not include that the vectors have a magnitude—that would be an additional requirement, giving what is called a normed vector space. More about that later.
To go from the familiar three-dimensional vector space to the vector spaces relevant to quantum mechanics, first the real numbers (components of the vector and possible multiplying factors) are to be generalized to complex numbers, and second the three-component vector goes an component vector. The consequent -dimensional complex space is sufficient to describe the quantum mechanics of angular momentum, an important subject. But to describe the wave function of a particle in a box requires an infinite dimensional space, one dimension for each Fourier component, and to describe the wave function for a particle on an infinite line requires the set of all normalizable continuous differentiable functions on that line. Fortunately, all these generalizations are to finite or infinite sets of complex numbers, so the mathematicians’ vector space requirements of commutativity and associativity are always trivially satisfied.
We use Dirac’s notation for vectors, and call them “kets”, so, in his language, if belong to the space, so does for arbitrary complex constants Since our vectors are made up of complex numbers, multiplying any vector by zero gives the null vector, and the additive inverse is given by reversing the signs of all the numbers in the vector.
Clearly, the set of solutions of Schrödinger’s equation for an electron in a potential satisfies the requirements for a vector space: is just a complex number at each point in space, so only complex numbers are involved in forming , and commutativity, associativity, etc., follow at once.
Vector Space Dimensionality
The vectors are linearly independent if
implies
A vector space is -dimensional if the maximum number of linearly independent vectors in the space is
Such a space is often called or if only real numbers are used.
Now, vector spaces with finite dimension are clearly insufficient for describing functions of a continuous variable But they are well worth reviewing here: as we’ve mentioned, they are fine for describing quantized angular momentum, and they serve as a natural introduction to the infinite-dimensional spaces needed to describe spatial wavefunctions.
A set of linearly independent vectors in -dimensional space is a basis: any vector can be written in a unique way as a sum over a basis:
You can check the uniqueness by taking the difference between two supposedly distinct sums: it will be a linear relation between independent vectors, a contradiction.
Since all vectors in the space can be written as linear sums over the elements of the basis, the sum of multiples of any two vectors has the form:
Inner Product Spaces
The vector spaces of relevance in quantum mechanics also have an operation associating a number with a pair of vectors, a generalization of the dot product of two ordinary three-dimensional vectors,
Following Dirac, we write the inner product of two ket vectors as . Dirac refers to this form as a “bracket” made up of a “bra” and a “ket”. This means that each ket vector has an associated bra For the case of a real -dimensional vector, have identical components—but we require for the more general case that
where * denotes complex conjugate. This implies that for a ket the bra will be . (Actually, bras are usually written as rows, kets as columns, so that the inner product follows the standard rules for matrix multiplication.) Evidently for the -dimensional complex vector is real and positive except for the null vector:
For the more general inner product spaces considered later we require to be positive, except for the null vector. (These requirements do restrict the classes of vector spaces we are considering—no Lorentz metric, for example—but they are all satisfied by the spaces relevant to nonrelativistic quantum mechanics.)
The norm of is then defined by
If is a member of so is , for any complex number
We require the inner product operation to commute with multiplication by a number, so
The complex conjugate of the right hand side is For consistency, the bra corresponding to the ket must therefore be -- in any case obvious from the definition of the bra in complex dimensions given above.
It follows that if
Constructing an Orthonormal Basis: the Gram-Schmidt Process
To have something better resembling the standard dot product of ordinary three vectors, we need that is, we need to construct an orthonormal basis in the space. There is a straightforward procedure for doing this called the Gram-Schmidt process. We begin with a linearly independent set of basis vectors, .
We first normalize by dividing it by its norm. Call the normalized vector Now cannot be parallel to because the original basis was of linearly independent vectors, but in general has a nonzero component parallel to equal to since is normalized. Therefore, the vector is perpendicular to as is easily verified. It is also easy to compute the norm of this vector, and divide by it to get the second member of the orthonormal basis. Next, we take and subtract off its components in the directions and normalize the remainder, and so on.
In an -dimensional space, having constructed an orthonormal basis with members any vector can be written as a column vector,
The corresponding bra is , which we write as a row vector with the elements complex conjugated, . This operation, going from columns to rows and taking the complex conjugate, is called taking the adjoint, and can also be applied to matrices, as we shall see shortly.
The reason for representing the bra as a row is that the inner product of two vectors is then given by standard matrix multiplication:
(Of course, this only works with an orthonormal base.)
The Schwartz Inequality
The Schwartz inequality is the generalization to any inner product space of the result (or ) for ordinary three-dimensional vectors. The equality sign in that result only holds when the vectors are parallel. To generalize to higher dimensions, one might just note that two vectors are in a two-dimensional subspace, but an illuminating way of understanding the inequality is to write the vector as a sum of two components, one parallel to and one perpendicular to . The component parallel to is just , so the component perpendicular to is the vector . Substituting this expression into , the inequality follows.
This same point can be made in a general inner product space: if are two vectors, then
is the component of perpendicular to , as is easily checked by taking its inner product with .
Then
Linear Operators
A linear operator takes any vector in a linear vector space to a vector in that space, and satisfies
with arbitrary complex constants.
The identity operator is (obviously!) defined by:
For an -dimensional vector space with an orthonormal basis since any vector in the space can be expressed as a sum , the linear operator is completely determined by its action on the basis vectors -- this is all we need to know. It’s easy to find an expression for the identity operator in terms of bras and kets.
Taking the inner product of both sides of the equation with the bra gives so
Since this is true for any vector in the space, it follows that that the identity operator is just
This is an important result: it will reappear in many disguises.
To analyze the action of a general linear operator we just need to know how it acts on each basis vector. Beginning with this must be some sum over the basis vectors, and since they are orthonormal, the component in the direction must be just
That is,
So if the linear operator acting on gives , that is, the linearity tells us that
where in the fourth step we just inserted the identity operator.
Since the ’s are all orthogonal, the coefficient of a particular on the left-hand side of the equation must be identical with the coefficient of the same on the right-hand side. That is,
Therefore the operator A is simply equivalent to matrix multiplication:
Evidently, then, applying two linear operators one after the other is equivalent to successive matrix multiplication—and, therefore, since matrices do not in general commute, nor do linear operators. (Of course, if we hope to represent quantum variables as linear operators on a vector space, this has to be true: the momentum operator certainly doesn’t commute with !)
Projection Operators
It is important to note that a linear operator applied successively to the members of an orthonormal basis might give a new set of vectors which no longer span the entire space. To give an example, the linear operator applied to any vector in the space picks out the vector’s component in the direction. It’s called a projection operator. The operator projects a vector into its components in the subspace spanned by the vectors and , and so on: if we extend the sum to be over the whole basis, we recover the identity operator.
Exercise: prove that the matrix representation of the projection operator has all elements zero except the first two diagonal elements, which are equal to one.
There can be no inverse operator to a nontrivial projection operator, since the information about components of the vector perpendicular to the projected subspace is lost.
The Adjoint Operator and Hermitian Matrices
As we’ve discussed, if a ket in the -dimensional space is written as a column vector with (complex) components, the corresponding bra is a row vector having as elements the complex conjugates of the ket elements. then follows automatically from standard matrix multiplication rules, and on multiplying by a complex number a to get (meaning that each element in the column of numbers is multiplied by ) the corresponding bra goes to
But suppose that instead of multiplying a ket by a number, we operate on it with a linear operator. What generates the parallel transformation among the bras? In other words, if what operator sends the bra to ? It must be a linear operator, because is linear, that is, if under A and then under Consequently, under the parallel bra transformation we must have the bra transformation is necessarily also linear. Recalling that the bra is an -element row vector, the most general linear transformation sending it to another bra is an matrix operating on the bra from the right.
This bra operator is called the adjoint of A, written That is, the ket has corresponding bra In an orthonormal basis, using the notation to denote the bra corresponding to the ket say,
So the adjoint operator is the transpose complex conjugate.
Important: for a product of two operators (prove this!),
An operator equal to its adjoint is called Hermitian. As we shall find in the next lecture, Hermitian operators are of central importance in quantum mechanics. An operator equal to minus its adjoint, , is anti-Hermitian (sometimes termed skew Hermitian). These two operator types are essentially generalizations of real and imaginary number: any operator can be expressed as a sum of a Hermitian operator and an anti-Hermitian operator,
The definition of adjoint naturally extends to vectors and numbers: the adjoint of a ket is the corresponding bra, the adjoint of a number is its complex conjugate. This is useful to bear in mind when taking the adjoint of an operator which may be partially constructed of vectors and numbers, such as projection-type operators. The adjoint of a product of matrices, vectors and numbers is the product of the adjoints in reverse order. (Of course, for numbers the order doesn’t matter.)
Unitary Operators
An operator is unitary if This implies first that operating on any vector gives a vector having the same norm, since the new norm . Furthermore, inner products are preserved, Therefore, under a unitary transformation the original orthonormal basis in the space must go to another orthonormal basis.
Conversely, any transformation that takes one orthonormal basis into another one is a unitary transformation. To see this, suppose that a linear transformation A sends the members of the orthonormal basis to the different orthonormal set , so etc. Then the vector will go to having the same norm, . A matrix elememt , but also . That is, for arbitrary kets . This is only possible if , so is unitary.
A unitary operation amounts to a rotation (possibly combined with a reflection) in the space. Evidently, since the adjoint rotates the basis back: it is the inverse operation, and so also, that is, U and commute.
Determinants
We review in this section the determinant of a matrix, a function closely related to the operator properties of the matrix.
Let’s start with matrices:
The determinant of this matrix is defined by:
Writing the two rows of the matrix as vectors:
( denotes row), is just the area (with appropriate sign) of the parallelogram having the two row vectors as adjacent sides:

This is zero if the two vectors are parallel (linearly dependent) and is not changed by adding any multiple of to (because the new parallelogram has the same base and the same height as the original—check this by drawing).
Let’s go on to the more interesting case of matrices:
The determinant of is defined as
where if any two are equal, +1 if (that is to say, an even permutation of 123) and 1 if is an odd permutation of Repeated suffixes, of course, imply summation here.
Writing this out explicitly,
Just as in two dimensions, it’s worth looking at this expression in terms of vectors representing the rows of the matrix
so
This is the volume of the parallelopiped formed by the three vectors being adjacent sides (meeting at one corner, the origin).
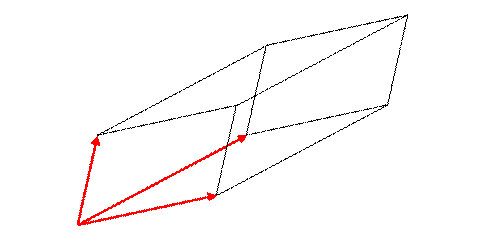
This parallelepiped volume will of course be zero if the three vectors lie in a plane, and it is not changed if a multiple of one of the vectors is added to another of the vectors. That is to say, the determinant of a matrix is not changed if a multiple of one row is added to another row. This is because the determinant is linear in the elements of a single row,
and the last term is zero because two rows are identical—so the triple vector product vanishes.
A more general way of stating this, applicable to larger determinants, is that for a determinant with two identical rows, the symmetry of the two rows, together with the antisymmetry of ensures that the terms in the sum all cancel in pairs.
Since the determinant is not altered by adding some multiple of one row to another, if the rows are linearly dependent, one row could be made identically zero by adding the right multiples of the other rows. Since every term in the expression for the determinant has one element from each row, the determinant would then be identically zero. For the three-dimensional case, the linear dependence of the rows means the corresponding vectors lie in a plane, and the parallelepiped is flat.
The algebraic argument generalizes easily to determinants: they are identically zero if the rows are linearly dependent.
The generalization from determinants is that becomes:
where is summed over all permutations of and the symbol is zero if any two of its suffixes are equal, for an even permutation and for an odd permutation. (Note: any permutation can be written as a product of swaps of neighbors. Such a representation is in general not unique, but for a given permutation, all such representations will have either an odd number of elements or an even number.)
An important theorem is that for a product of two matrices the determinant of the product is the product of the determinants, This can be verified by brute force for matrices, and a proof in the general case can be found in any book on mathematical physics (for example, Byron and Fuller).
It can also be proved that if the rows are linearly independent, the determinant cannot be zero.
(Here’s a proof: take an matrix with the row vectors linearly independent. Now consider the components of those vectors in the dimensional subspace perpendicular to These vectors, each with only components, must be linearly dependent, since there are more of them than the dimension of the space. So we can take some combination of the rows below the first row and subtract it from the first row to leave the first row and cannot be zero since we have a matrix with linearly independent rows. We can then subtract multiples of this first row from the other rows to get a determinant having zeros in the first column below the first row. Now look at the determinant to be multiplied by Its rows must be linearly independent since those of the original matrix were. Now proceed by induction.)
To return to three dimensions, it is clear from the form of
that we could equally have taken the columns of as three vectors, in an obvious notation, , and linear dependence among the columns will also ensure the vanishing of the determinant—so, in fact, linear dependence of the columns ensures linear dependence of the rows.
This, too, generalizes to : in the definition of determinant , the row suffix is fixed and the column suffix goes over all permissible permutations, with the appropriate sign—but the same terms would be generated by having the column suffixes kept in numerical order and allowing the row suffix to undergo the permutations.
An Aside: Reciprocal Lattice Vectors
It is perhaps worth mentioning how the inverse of a matrix operator can be understood in terms of vectors. For a set of linearly independent vectors , a reciprocal set can be defined by
and the obvious cyclic definitions for the other two reciprocal vectors. We see immediately that
from which it follows that the inverse matrix to
.
(These reciprocal vectors are important in x-ray crystallography, for example. If a crystalline lattice has certain atoms at positions , where are integers, the reciprocal vectors are the set of normals to possible planes of the atoms, and these planes of atoms are the important elements in the diffractive x-ray scattering.)
Eigenkets and Eigenvalues
If an operator operating on a ket gives a multiple of the same ket,
then is said to be an eigenket (or, just as often, eigenvector, or eigenstate!) of with eigenvalue .
Eigenkets and eigenvalues are of central importance in quantum mechanics: dynamical variables are operators, a physical measurement of a dynamical variable yields an eigenvalue of the operator, and forces the system into an eigenket.
In this section, we shall show how to find the eigenvalues and corresponding eigenkets for an operator We’ll use the notation for the set of eigenkets with corresponding eigenvalues (Obviously, in the eigenvalue equation here the suffix is not summed over.)
The first step in solving is to find the allowed eigenvalues
Writing the equation in matrix form,
This equation is actually telling us that the columns of the matrix are linearly dependent! To see this, write the matrix as a row vector each element of which is one of its columns, and the equation becomes
which is to say
the columns of the matrix are indeed a linearly dependent set.
We know that means the determinant of the matrix is zero,
Evaluating the determinant using gives an order polynomial in sometimes called the characteristic polynomial. Any polynomial can be written in terms of its roots:
where the ’s are the roots of the polynomial, and C is an overall constant, which from inspection of the determinant we can see to be (It’s the coefficient of ) The polynomial roots (which we don’t yet know) are in fact the eigenvalues. For example, putting in the matrix, which means that has a nontrivial solution and this is our eigenvector
Notice that the diagonal term in the determinant generates the leading two orders in the polynomial , (and some lower order terms too). Equating the coefficient of here with that in ,
Putting in both the determinantal and the polynomial representations (in other words, equating the -independent terms),
So we can find both the sum and the product of the eigenvalues directly from the determinant, and for a matrix this is enough to solve the problem.
For anything bigger, the method is to solve the polynomial equation to find the set of eigenvalues, then use them to calculate the corresponding eigenvectors. This is done one at a time.
Labeling the first eigenvalue found as the corresponding equation for the components of the eigenvector is
This looks like equations for the numbers but it isn’t: remember the rows are linearly dependent, so there are only independent equations. However, that’s enough to determine
the ratios of the vector components then finally the eigenvector is normalized. The process is then repeated for each eigenvalue. (Extra care is needed if the polynomial has coincident roots—we’ll discuss that case later.)
Eigenvalues and Eigenstates of Hermitian Matrices
For a Hermitian matrix, it is easy to establish that the eigenvalues are always real. (Note: A basic postulate of Quantum Mechanics, discussed in the next lecture, is that physical observables are represented by Hermitian operators.) Taking (in this section) to be hermitian, and labeling the eigenkets by the eigenvalue, that is,
the inner product with the bra gives But the inner product of the adjoint equation (remembering )
with gives so , and all the eigenvalues must be real.
They certainly don’t have to all be different: for example, the unit matrix is Hermitian, and all its eigenvalues are of course But let’s first consider the case where they are all different.
It’s easy to show that the eigenkets belonging to different eigenvalues are orthogonal.
If
take the adjoint of the first equation and then the inner product with , and compare it with the inner product of the second equation with :
so unless the eigenvalues are equal. (If they are equal, they are referred to as degenerate eigenvalues.)
Let’s first consider the nondegenerate case: has all eigenvalues distinct. The eigenkets of appropriately normalized, form an orthonormal basis in the space.
Write
Now
so
Note also that, obviously, is unitary:
We have established, then, that for a Hermitian matrix with distinct eigenvalues (nondegenerate case), the unitary matrix having columns identical to the normalized eigenkets of diagonalizes that is, is diagonal. Furthermore, its (diagonal) elements equal the corresponding eigenvalues of
Another way of saying this is that the unitary matrix is the transformation from the original orthonormal basis in the space to the basis formed of the normalized eigenkets of
Proof that the Eigenvectors of a Hermitian Matrix Span the Space
We’ll now move on to the general case: what if some of the eigenvalues of are the same? In this case, any linear combination of them is also an eigenvector with the same eigenvalue. Assuming they form a basis in the subspace, the Gram Schmidt procedure can be used to make it orthonormal, and so part of an orthonormal basis of the whole space.
However, we have not actually established that the eigenvectors do form a basis in a degenerate subspace. Could it be that (to take the simplest case) the two eigenvectors for the single eigenvalue turn out to be parallel? This is actually the case for some 2×2 matrices—for example, , we need to prove it is not true for Hermitian matrices, and nor are the analogous statements for higher-dimensional degenerate subspaces.
A clear presentation is given in Byron and Fuller, section 4.7. We follow it here. The procedure is by induction from the case. The general Hermitian matrix has the form
where are real. It is easy to check that if the eigenvalues are degenerate, this matrix becomes a real multiple of the identity, and so trivially has two orthonormal eigenvectors. Since we already know that if the eigenvalues of a Hermitian matrix are distinct it can be diagonalized by the unitary transformation formed from its orthonormal eigenvectors, we have established that any Hermitian matrix can be so diagonalized.
To carry out the induction process, we now assume any Hermitian matrix can be diagonalized by a unitary transformation. We need to prove this means it’s also true for an Hermitian matrix (Recall a unitary transformation takes one complete orthonormal basis to another. If it diagonalizes a Hermitian matrix, the new basis is necessarily the set of orthonormalized eigenvectors. Hence, if the matrix can be diagonalized, the eigenvectors do span the -dimensional space.)
Choose an eigenvalue of with normalized eigenvector (We put in for transpose, to save the awkwardness of filling the page with a few column vectors.) We construct a unitary operator by making this the first column, then filling in with other normalized vectors to construct, with , an -dimensional orthonormal basis.
Now, since , the first column of the matrix will just be , and the rows of the matrix will be followed by normalized vectors orthogonal to it, so the first column of the matrix will be followed by zeros. It is easy to check that is Hermitian, since is, so its first row is also zero beyond the first diagonal term.
This establishes that for an Hermitian matrix, a unitary transformation exists to put it in the form:
But we can now perform a second unitary transformation in the subspace orthogonal to (this of course leaves invariant), to complete the full diagonalization -- that is to say, the existence of the diagonalization, plus the argument above, guarantees the existence of the diagonalization: the induction is complete.
Diagonalizing a Hermitian Matrix
As discussed above, a Hermitian matrix is diagonal in the orthonormal basis of its set of eigenvectors: , since
If we are given the matrix elements of in some other orthonormal basis, to diagonalize it we need to rotate from the initial orthonormal basis to one made up of the eigenkets of
Denoting the initial orthonormal basis in the standard fashion
the elements of the matrix are .
A transformation from one orthonormal basis to another is a unitary transformation, as discussed above, so we write it
Under this transformation, the matrix element
So we can find the appropriate transformation matrix by requiring that be diagonal with respect to the original set of basis vectors. (Transforming the operator in this way, leaving the vector space alone, is equivalent to rotating the vector space and leaving the operator alone. Of course, in a system with more than one operator, the same transformation would have to be applied to all the operators).
In fact, just as we discussed for the nondegenerate (distinct eigenvalues) case, the unitary matrix we need is just composed of the normalized eigenkets of the operator
and it follows as before that
(The repeated suffixes here are of course not summed over.)
If some of the eigenvalues are the same, the Gram Schmidt procedure may be needed to generate an orthogonal set, as mentioned earlier.
Functions of Matrices
The same unitary operator that diagonalizes an Hermitian matrix will also diagonalize because
so
Evidently, this same process works for any power of and formally for any function of expressible as a power series, but of course convergence properties need to be considered, and this becomes trickier on going from finite matrices to operators on infinite spaces.
Commuting Hermitian Matrices
From the above, the set of powers of an Hermitian matrix all commute with each other, and have a common set of eigenvectors (but not the same eigenvalues, obviously). In fact it is not difficult to show that any two Hermitian matrices that commute with each other have the same set of eigenvectors (after possible Gram Schmidt rearrangements in degenerate subspaces).
If two Hermitian matrices commute, that is, and has a nondegenerate set of eigenvectors then that is, is an eigenvector of with eigenvalue Since is nondegenerate, must be some multiple of , and we conclude that have the same set of eigenvectors.
Now suppose is degenerate, and consider the subspace spanned by the eigenvectors of having eigenvalue Applying the argument in the paragraph above, must also lie in this subspace. Therefore, if we transform with the same unitary transformation that diagonalized will not in general be diagonal in the subspace but it will be what is termed block diagonal, in that if operates on any vector in it gives a vector in .
can be written as two diagonal blocks: one , one with zeroes outside these diagonal blocks, for example, for
And, in fact, if there is only one degenerate eigenvalue that second block will only have nonzero terms on the diagonal:
therefore operates on two subspaces, one -dimensional, one -dimensional, independently—a vector entirely in one subspace stays there.
This means we can complete the diagonalization of with a unitary operator that only operates on the block . Such an operator will also affect the eigenvectors of but that doesn’t matter, because all vectors in this subspace are eigenvectors of with the same eigenvalue, so as far as is concerned, we can choose any orthonormal basis we like—the basis vectors will still be eigenvectors.
This establishes that any two commuting Hermitian matrices can be diagonalized at the same time. Obviously, this can never be true of noncommuting matrices, since all diagonal matrices commute.
Diagonalizing a Unitary Matrix
Any unitary matrix can be diagonalized by a unitary transformation. To see this, recall that any matrix M can be written as a sum of a Hermitian matrix and an anti-Hermitian matrix,
where both A, B are Hermitian. This is the matrix analogue of writing an arbitrary complex number as a sum of real and imaginary parts.
If commute, they can be simultaneously diagonalized (see the previous section), and therefore can be diagonalized. Now, if a unitary matrix is expressed in this form with Hermitian, it easily follows from that commute, so any unitary matrix can be diagonalized by a unitary transformation. More generally, if a matrix commutes with its adjoint , it can be diagonalized.
(Note: it is not possible to diagonalize unless both and are simultaneously diagonalized. This follows from being Hermitian and anti-Hermitian for any unitary operator so their off-diagonal elements cannot cancel each other, they must all be zero if has been diagonalized by in which case the two transformed matrices are diagonal, therefore commute, and so do the original matrices )
It is worthwhile looking at a specific example, a simple rotation of one orthonormal basis into another in three dimensions. Obviously, the axis through the origin about which the basis is rotated is an eigenvector of the transformation. It’s less clear what the other two eigenvectors might be—or, equivalently, what are the eigenvectors corresponding to a two dimensional rotation of basis in a plane? The way to find out is to write down the matrix and diagonalize it.
The matrix
Note that the determinant is equal to unity. The eigenvalues are given by solving
The corresponding eigenvectors satisfy
The eigenvectors, normalized, are:
Note that, in contrast to a Hermitian matrix, the eigenvalues of a unitary matrix do not have to be real. In fact, from , sandwiched between the bra and ket of an eigenvector, we see that any eigenvalue of a unitary matrix must have unit modulus—it’s a complex number on the unit circle. With hindsight, we should have realized that one eigenvalue of a two-dimensional rotation had to be , the product of two two-dimensional rotations is given be adding the angles of rotation, and a rotation through changes all signs, so has eigenvalue Note that the eigenvector itself is independent of the angle of rotation: in two dimensions, the rotations all commute, so they must have common eigenvectors. Successive rotation operators applied to the plus eigenvector add their angles, when applied to the minus eigenvector, all angles are subtracted.