is related to the experimental asymmetry through
where f is the dilution factor that includes the effect of the unpolarized nuclei (see the discussion around Eq.(10).
The uncertainty 
can therefore be expressed as
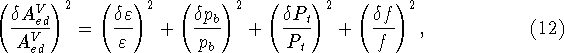
which is a valid expansion since these uncertainties are uncorrelated. From
, one can obtain the exact expression
which can be approximated as 
,
for the usual case of small
(implying 
). Therefore
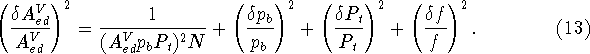
It is expected that at CEBAF the beam polarization will be measured with an
accuracy of better than 4%, as it has been done at other laboratories[11]. We expect the
situation to improve such that we have used 2% in our estimates. The target polarization
has been determined to 
in current designs, but, based on CERN experience, we
expect to ultimately do better.
The magnitude of is determined by the requirement that it should allow
to discriminate among the various models for 
,
and it has to be consistent with the lower limits imposed by the uncertainties 
, and 
. Moreover, it should not represent an unreasonably large
number of counts.
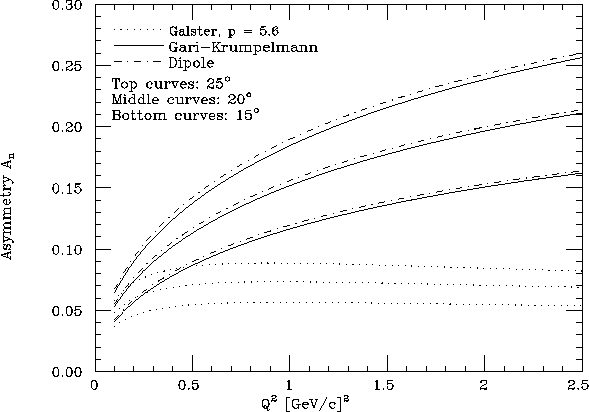
Figure 11: A as a function of Q 
for three models and three angles.
From Figure 12
it can be seen that to distinguish, for example,
between the Galster parametrization and the Gari-Krümpelmann (G-K) model in the
kinematic region of interest, has to be of the order of 
at the low
points, to 
on the high momentum transfer side, for a four standard
deviation (or better) separation between models. Taking as reference the Galster model,
Table 5
illustrates the magnitude of the expected uncertainties in the asymmetry , the
experimental asymmetry
and the number of counts needed for the desired level of precision. In this
table, the values of N were computed using the following additional assumptions: 
, 
.
These values of N have been calculated using the expression
We note that the minimum uncertainty in
is restricted by the combined uncertainties in 
, and f which in the
present case amount to 
.
To obtain from the asymmetry, we have to solve the expression for
(Equation (5))
for the ratio 
. Since the different models predict that as
increases, this ratio approaches and even exceeds 1 (
at 
(GeV/c) in the dipole and G-K models), it is
inaccurate to neglect the term 
in the range of the present
proposal. The result is that we have a quadratic equation for that can be written
as
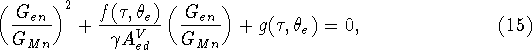
where 
, and
. The solutions are
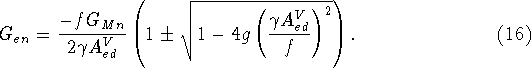
By substituting in this expression the asymmetry predicted by a given model,
it is seen that the negative root reproduces . Therefore we can write
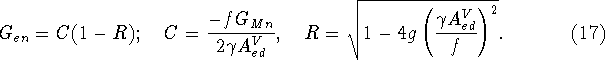
The purpose of this exercise is to obtain an expression for 
,
based on the usual expansion for the uncertainties
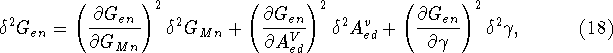
where the uncertainties 
have been neglected
given their very small relative magnitudes.
After the appropriate substitutions are made, we find that
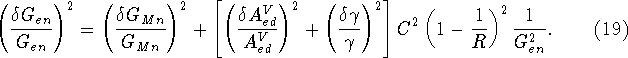
This equation contains the effects of both the uncertainty in 
as
well as the propagation of the uncertainty in the asymmetry.
In Table 6 shows that for the considered earlier, there is a
significant effect on . The uncertainty in was taken to be 5%, combining
our present knowledge of this quantity at the values of this proposal, with the
improved precision for Q 
1 (GeV/c) expected from the ongoing measurements of
the Basel group is performing at Mainz.
We note that in the estimates given above we have taken care of the nonlinear relationship
between the asymmetry and G (see Equation 5).
This nonlinearity results from the fact that for small values of G A is proportional
to G, while for very large values and large momentum transfer A depends on
G 
. There obviously is a range where A does not at all depend on G! This
however does not imply that a measurement of A is not useful; one simply has to analyse
the data in a different way. The nominator of equation
5 always depends linearly of G. One therefore can determine G directly from
, and not from A= / 
. This requires the knowledge of the detector
efficiency, which can be deduced from a short cross section measurement under kinematics
where the cross section is dominated by
G. The error bars of figure 13 for the case where the data would correspond
to something like Gari-Krumpelman (where at large momentum transfer the blow-up factor
becomes of order 2) therefore can significantly be reduced.
