Introducing Waves: Strings and Springs

Michael Fowler

One-Dimensional Traveling Waves

The most important kinds of traveling waves in everyday life are electromagnetic waves, sound waves, and perhaps water waves, depending on where you live. (Electromagnetic waves include X-rays, light, heat, microwaves, radio, etc.) But it’s tough to analyze waves spreading out in three dimensions, reflecting off objects, etc., so we begin with the simplest interesting examples of waves, those restricted to move along a line.

Let’s start with a rope, like a clothesline, stretched between two hooks. You take one end off the hook, holding the rope, and, keeping it stretched fairly tight, wave your hand up and back once. If you do it fast enough, you’ll see a single bump travel along the rope:

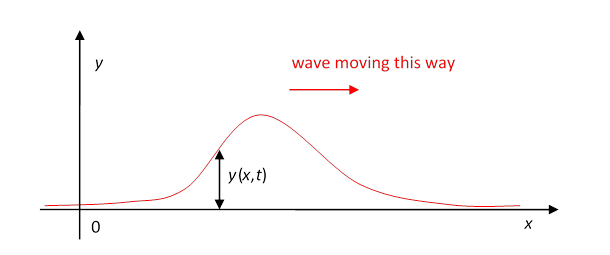
This is the simplest example of a traveling wave. You can make waves of different shapes by moving your hand up and down in different patterns, for example an upward bump followed by a dip, or two bumps. You’ll find that the traveling wave keeps the same shape as it moves down the rope. (That’s before it reaches the end, of course $—$ things get more complicated at that point $—$ we’ll discuss it later.)

Taking the rope to be stretched tightly enough that we can take it to be horizontal, we’ll use its rest position as our $x$ -axis (see the diagram above). The $y$ -axis is taken vertically upwards, and we only wave the rope in an up-and-down way, so actually $y (x, t)$ will be how far the rope is from its rest position at $x$ at time $t :$ that is, the graph $y (x, t)$ above just shows where the rope is at time $t .$

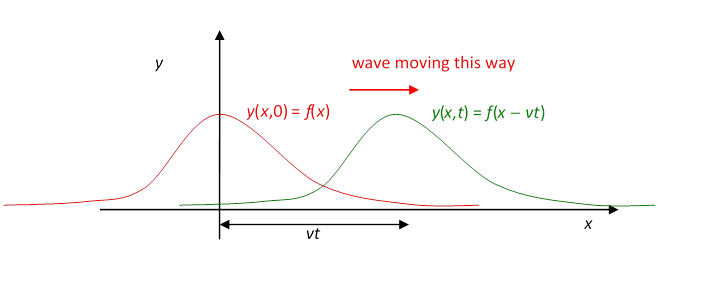
We can now express the observation that the wave “keeps the same shape” more precisely. Taking for convenience time $t = 0$ to be the moment when the peak of the wave passes $x = 0,$ we graph here the rope’s position at $t = 0$ (red) and some later time $t$ (green). Denoting the first function by $y (x, 0) = f (x),$ then the second $y (x, t) = f (x - v t) :$ it’s the same function $—$ the “same shape” $—$ but moved over by $v t,$ where $v$ is the velocity of the wave.

To summarize: on sending a traveling wave down a rope by jerking the end up and down, from observation the wave travels at constant speed and keeps its shape, so the displacement $y$ of the rope at any horizontal position at $x$ at time $t$ has the form

$y (x, t) = f (x - v t) .$

(We’re neglecting frictional effects $—$ in a real rope, the bump gradually gets smaller as it moves along.)

Transverse and Longitudinal Waves

The wave on a rope described above is called a transverse wave, because, as the wave passes, the motion of any actual bit of rope is in the $y$ -direction, at right angles (transverse) to the direction of the wave itself, which is of course along the rope.

A different kind of wave is possible: consider a series of balls in a line connected by springs, and give the ball on the far left a sudden push to the right. A wave of compression will move down the line:

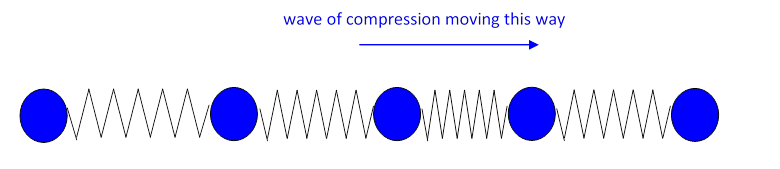
In this case, the motion of each ball as the wave passes through is in the same direction as the wave. In fact, this happens as a sound wave travels through air: it’s a longitudinal wave.

Traveling and Standing Waves

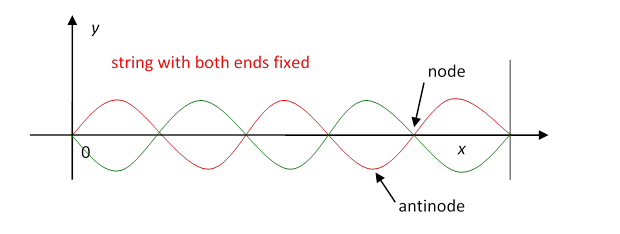
Both the waves considered above are traveling waves. Another familiar kind of wave is that generated on a string fixed at both ends when it is made to vibrate. We found in class that for certain frequencies the string vibrated in a sine-wave pattern, as illustrated below, with no vibration at the ends, of course, but also no vibration at a series of equally-spaced points between the ends: these quiet places we term nodes. The places of maximum oscillation are antinodes.

We found a sequence of these standing waves on increasing the driving frequency, having 0, 1, 2, 3, … nodes. The red and green curves indicate the string position at successive times.

Almost all musical instruments generate standing waves: the piano has standing waves on strings, the organ generates standing waves in the air in pipes. Other instruments are more complicated: although the sound of a violin comes from a vibrating string, resonance with the rest of the instrument gives rise to complicated standing wave patterns. An excellent discussion and demonstration can be found at //www.phys.unsw.edu.au/music/violin/ , along with links to similar pages for other instruments, and many aspects of sound and music.

previous index next