The Pendulum

Michael Fowler

The Simple Pendulum

Galileo was the first to record that the period of a swinging lamp high in a cathedral was independent of the amplitude of the oscillations, at least for the small amplitudes he could observe. In 1657, Huygens constructed the first pendulum clock, a vast improvement in timekeeping over all previous techniques. So the pendulum was the first oscillator of real technological importance.

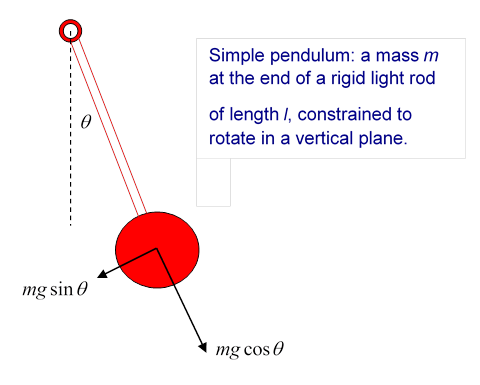
In fact, though, the pendulum is not quite a simple harmonic oscillator: the period does depend on the amplitude, but provided the angular amplitude is kept small, this is a small effect.

The weight mg of the bob (the mass at the end of the light rod) can be written in terms of components parallel and perpendicular to the rod. The component parallel to the rod balances the tension in the rod. The component perpendicular to the rod accelerates the bob,

$m l \frac{d^{2} θ}{d t^{2}} = - m g \sin θ .$

The mass cancels between the two sides, pendulums of different masses having the same length behave identically. (In fact, this was one of the first tests that inertial mass and gravitational mass are indeed equal: pendulums made of different materials, but the same length, had the same period.)

For small angles, the equation is close to that for a simple harmonic oscillator,

$l \frac{d^{2} θ}{d t^{2}} = - g θ,$

with frequency $ω = \sqrt{g / l}$ , that is, time of one oscillation $T = 2 π \sqrt{l / g} .$ At a displacement of ten degrees, the simple harmonic approximation overestimates the restoring force by around one part in a thousand, and for smaller angles this error goes essentially as the square of the angle. So a pendulum clock designed to keep time with small oscillations of the pendulum will gain four seconds an hour or so if the pendulum is made to swing with a maximum angular displacement of ten degrees.

The potential energy of the pendulum relative to its rest position is just mgh, where h is the height difference, that is, $m g l (1 - \cos θ) .$ The total energy is therefore

$E = \frac{1}{2} m {(l \frac{d θ}{d t})}^{2} + m g l (1 - \cos θ) ≅ \frac{1}{2} m {(l \frac{d θ}{d t})}^{2} + \frac{1}{2} m g l θ^{2}$

for small angles.

Pendulums of Arbitrary Shape

The analysis of pendulum motion in terms of angular displacement works for any rigid body swinging back and forth about a horizontal axis under gravity. For example, consider a rigid rod.

The kinetic energy is given by $\frac{1}{2} I {\dot{θ}}^{2},$ where $I$ is the moment of inertia of the body about the rod, the potential energy is $m g l (1 - \cos θ)$ as before, but $l$ is now the distance of the center of mass from the axis.

The equation of motion is that the rate of change of angular momentum equals the applied torque,

$I \ddot{θ} = - m g l \sin θ$ ,

for small angles the period $T = 2 π \sqrt{I / m g l}$ , and for the simple pendulum we considered first $I = m l^{2},$ giving the previous result.

Variation of Period of a Pendulum with Amplitude

As the amplitude of pendulum motion increases, the period lengthens, because the restoring force $- m g \sin θ$ increases more slowly than $- m g θ$ ( $\sin θ ≅ θ - θ^{3} / 3!$ for small angles).

The simplest way to get some idea how this happens is to explore it with the accompanying spreadsheet.

Begin with an initial displacement of 0.1 radians (5.7 degrees):

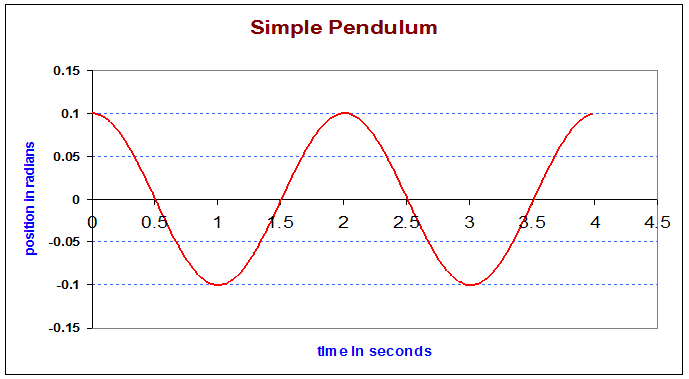
Next, try one radian:

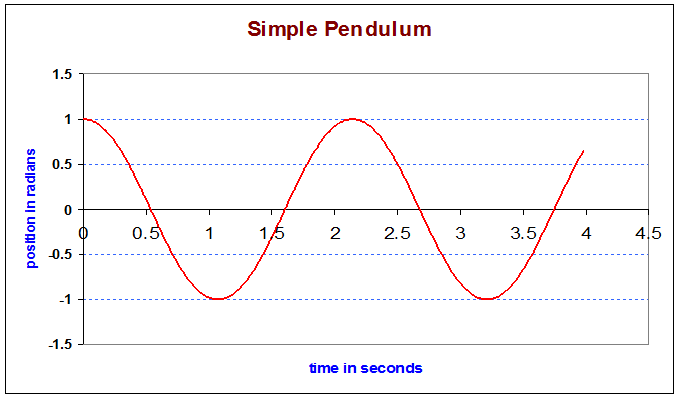
The change in period is a little less that 10%, not too dramatic considering the large amplitude of this swing.

Two radians gives an increase around 35%, and three radians amplitude increases the period almost threefold.

It’s well worth exploring further with the spreadsheet!

previous index next